Questão 1
(Unesp) O primeiro cientista que estudou a influência da temperatura sobre a velocidade das reações foi Jacobus van’t Hoff, no final do século XIX. Ele chegou por meio de seus estudos à seguinte regra empírica:
Regra de van’t Hoff: um aumento de 10 °C na temperatura em que uma reação química ocorre faz com que a velocidade da reação dobre.
(https://mundoeducacao.uol.com.br. Adaptado.)
Uma pessoa cozinhou 0,5 kg de feijão-preto em uma panela comum ao nível do mar. Esse cozimento levou 3 horas, a partir da ebulição da água.
Considerando a regra de Van’t Hoff e que em uma panela de pressão a temperatura de ebulição da água pode chegar a 120 °C, caso essa pessoa tivesse utilizado uma panela de pressão para cozinhar o feijão, o tempo de cozimento seria cerca de
A) 15 min.
B) 39 min.
C) 45 min.
D) 60 min.
E) 75 min.
Questão 2
(UVV) A tabela abaixo expressa os valores dos números de mol dos reagentes e produtos ao longo de 10 minutos:
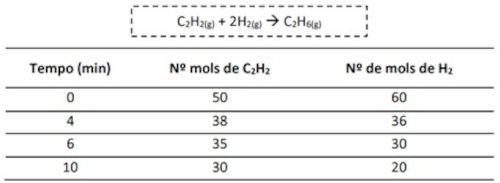
Qual é a velocidade de decomposição de H2 nos primeiros 10 minutos de reação?
A) 2,0 mols.min−1.
B) 4,0 mols.min−1.
C) 5,0 mols.min−1.
D) 5,4 mols.min−1.
E) 6,0 mols.min−1.
Questão 3
(UVV) A partir da equação não balanceada abaixo e considerando que a velocidade de consumo do ferro é de 2,5 mol/min, determine a velocidade de formação do óxido férrico:
Fe (s) + O2 (g) → Fe2O3 (s)
A) Fe2O3 é de 1,25 mol/min.
B) Fe2O3 é de 2,50 mol/min.
C) Fe2O3 é de 3,45 mol/min.
D) Fe2O3 é de 5,20 mol/min.
E) Fe2O3 é de 6,25 mol/min.
Questão 4
(Cesmac) Na assepsia de ferimentos, comumente, é utilizado o peróxido de hidrogênio (H2O2). Sua ação desinfetante ocorre devido à reação com a enzima catalase, presente em meio celular, a qual promove a decomposição do H2O2 em oxigênio gasoso e água, justificando a formação de bolhas sob o ferimento. Na reação de decomposição do peróxido de hidrogênio, a concentração de H2O2 foi monitorada com relação ao tempo:

Baseado nos dados apresentados acima, qual a velocidade média em mol.L−1.s−1 para a reação de decomposição do H2O2?
A) 1,0
B) 0,01
C) 0,3
D) 0,005
E) 0,6
Questão 5
A produção de metanol pode ser feita por meio da reação de hidrogenação do monóxido de carbono, conforme demonstrado a seguir.
CO (g) + 2 H2 (g) → CH3OH (g)
Em um reator de capacidade volumétrica igual a 2,0 L, constatou-se a produção de 0,4 mol de metanol em 10 minutos. Nesse contexto, a velocidade média de consumo de H2, em mol/L.min foi igual a:
A) 0,02
B) 0,04
C) 0,08
D) 0,16
E) 0,32
Questão 6
O nitrato de amônio é um composto cuja decomposição térmica (termólise) é muito exotérmica, causando explosões impressionantes. A reação da termólise do nitrato de amônio é demonstrada na equação química a seguir.
6 NH4NO3 → N2O + 10 H2O + NH4NO3 + 3 N2 + 2 NO2
Os valores a seguir demonstram a variação de concentração em função do tempo de uma termólise de nitrato de amônio reproduzida em laboratório.
|
Tempo |
Concentração |
|
0 s |
0,90 mol/L |
|
180 s |
0,60 mol/L |
|
300 s |
0,45 mol/L |
A partir do que foi exposto, é possível afirmar que:
A) Entre 180 e 300 s, a velocidade de formação do gás nitrogênio é igual a 1,25 x 10−3 mol/L.s
B) A velocidade de consumo de nitrato de amônio é maior que a velocidade de produção de H2O nos 300 segundos iniciais.
C) Nos 300 segundos iniciais, a velocidade de produção de NO2 é de 5 x 10−4 mol/L.s.
D) A velocidade de consumo de nitrato de amônio nos 300 segundos iniciais é de, aproximadamente, 3 x 10−3 mol/L.s.
E) A velocidade de formação de N2O é menor nos 180 segundos iniciais se comparado ao intervalo entre 180 e 300 segundos.
Questão 7
O processo de síntese da amônia rendeu ao químico alemão Fritz Haber o prêmio Nobel de Química de 1918. Sua adaptação para a indústria química foi feita por Carl Bosch, o qual ganhou o Nobel de Química de 1931 por tal feito.
A reação de síntese da amônia é dada pela seguinte equação balanceada:
N2 (g) + 3 H2 (g) ⇌ 2 NH3 (g)
Sabendo que, em laboratório, foi percebido o consumo de 6 mols de N2 por minuto, é possível dizer que o consumo de H2 é igual a:
A) 6 mols por minuto.
B) 12 mols por minuto.
C) 18 mols por minuto.
D) 24 mols por minuto.
E) 36 mols por minuto.
Questão 8
A decomposição do peróxido de hidrogênio, H2O2, ocorre muito rapidamente na presença de luz e calor. Por essas e outras é esse composto é armazenado em frascos opacos e em ambientes que não estejam expostos ao calor. A decomposição é demonstrada pela seguinte equação:
H2O2 → H2O + ½ O2
Foi medido o tempo da decomposição do peróxido de hidrogênio em dada temperatura para melhor entendimento do processo:
|
Tempo (min) |
Concentração H2O2 (mol/L) |
|
0 |
1,00 |
|
20 |
0,96 |
|
40 |
0,93 |
|
60 |
0,90 |
A partir dos dados da tabela, é possível concluir que a velocidade média de consumo de H2O2 após uma hora de experimento é igual a:
A) 1,67 x 10−3 mol/L.h
B) 0,10 mol/L.h
C) 0,04 mol/L.h
D) 1,33 x 10−2 mol/L.h
E) 0,02 mol/L.h
Questão 9
Pastilhas para combate da má digestão e da azia podem ser feitas de bicarbonato de sódio, NaHCO3 (MM = 84 g/mol). Para entender melhor o tempo de dissolução dessas pastilhas, um laboratório farmacêutico resolveu dissolver 504 g de bicarbonato de sódio em um frasco com 200 mL de ácido clorídrico, o mesmo ácido do nosso estômago. A equação química que ocorre é a que se segue:
NaHCO3 + HCl → NaCl + H2O + CO2
Sabendo que a amostra se dissolveu em um segundo, assinale a alternativa que possui a velocidade de formação de CO2, em mol/L.s.
A) 30
B) 60
C) 120
D) 180
E) 240
Questão 10
Óxidos de nitrogênio são um grande problema ambiental. São poluentes que podem atuar, por exemplo, na intensificação da acidez da chuva. Em camadas da atmosfera, o gás NO pode ser convertido ao gás NO2 por meio da reação com o gás oxigênio.
NO (g) + ½ O2 (g) ⇌ NO2 (g)
A tabela a seguir demonstra a variação de oxigênio para essa reação, em um ambiente controlado e em dada temperatura.
|
O2 (mol/L) |
Tempo (s) |
|
0,030 |
0 |
|
0,027 |
60 |
|
0,020 |
180 |
|
0,015 |
240 |
|
0,012 |
360 |
Assinale a alternativa que contém a velocidade média da reação, no intervalo de 1 até 4 minutos, em mol/L.min.
A) 0,004
B) 0,006
C) 0,008
D) 0,010
E) 0,012
Questão 11
O ácido hidrazoico, HN3, é um composto líquido volátil e bastante explosivo. Sua decomposição é dada a seguir.
2 HN3 → H2 + 3 N2
Sabendo que, em determinado estudo desse ácido, o ácido hidrazoico foi decomposto em uma velocidade de 3,0 x 10−3 mol/L.min, assinale a alternativa que contém a velocidade de produção, em mol/L.min, dos gases hidrogênio e nitrogênio, respectivamente.
A) 3,0 x 10−3 e 4,5 x 10−3
B) 1,5 x 10−3 e 1,5 x 10−3
C) 3,0 x 10−3 e 1,5 x 10−3
D) 1,5 x 10−3 e 4,5 x 10−3
E) 4,5 x 10−3 e 3,0 x 10−3
Questão 12
O gás butano está na constituição do GLP, gás liquefeito de petróleo, o conhecido gás de botijão, amplamente empregado em residências brasileiras para cozimento de alimentos. Durante a utilização do fogão, a reação que ocorre é a da combustão do butano, conforme equação a seguir.
C4H10 + 13/2 O2 → 4 CO2 + 5 H2O
Supondo que a velocidade média de consumo durante o preparo de um prato tenha sido de 0,01 mol de butano por minuto, assinale a alternativa que contém a massa de CO2 (44 g/mol) produzida, em gramas.
A) 2,4
B) 44,0
C) 52,8
D) 88,0
E) 105,6
Resposta Questão 1
Alternativa C.
Segundo a regra de Van’t Hoff, um aumento de 10 °C na temperatura significa que a velocidade da reação dobra. A temperatura de ebulição da água é de 100 °C e, nessas condições, o cozimento de 0,5 kg de feijão-preto levou 3 horas.
Aumentando-se a temperatura para 120 °C, segundo a regra de Van’t Hoff, a velocidade deve duplicar a cada aumento de 10 °C. Ou seja, a 110 °C ela dobra e a 120 °C ela dobra novamente, o que quer dizer que, em relação à ebulição, a velocidade se torna 4 vezes maior.
Se a velocidade se torna 4 vezes maior, então o tempo de cozimento se torna 4 vezes menor. Como o tempo de cozimento a 100 °C foi de 3 horas (180 min), então o tempo de cozimento em 120 °C será de 180/4, que é igual a 45 minutos.
Resposta Questão 2
Alternativa B.
A velocidade de decomposição de H2 nos primeiros 10 minutos é dada pela seguinte fórmula:
\(v = \frac{|\Delta H_2|}{\Delta t} = \frac{|20 - 60|}{10 - 0} = \frac{40}{10} = 4\ \frac{mol}{min}\)
Resposta Questão 3
Alternativa A.
A reação balanceada fica da seguinte forma:
2 Fe (s) + 3/2 O2 (g) → Fe2O3 (s)
Assim sendo, como o coeficiente estequiométrico de ferro é o dobro de Fe2O3, é possível dizer que a velocidade de consumo de ferro é o dobro da velocidade de produção de Fe2O3.
Por isso, como a velocidade de consumo de ferro é igual a 2,5 mol/min, então a velocidade de produção de Fe2O3 é igual a 1,25 mol/min.
Resposta Questão 4
Alternativa D.
Como os dados informam 3 minutos, então o tempo a ser considerado é de 180 segundos. A velocidade média de H2O2 é dada pela expressão:
\(v_m = \frac{|\Delta {[H_2O_2]}|}{\Delta t} = \frac{|1,1- 2,0|}{180- 0} = \frac{0,9}{180} = 0,005\ \frac{mol}{L\cdot s}\)
Resposta Questão 5
Alternativa B.
Ao se observar a equação química balanceada, percebe-se que o coeficiente estequiométrico do gás hidrogênio é o dobro do metanol e, assim sendo, seu consumo reacional também será o dobro. Logo, se foram produzidos 0,4 mol de metanol em 10 minutos, então foram consumidos 2 x 0,4 mol de H2, ou seja, 0,8 mol. A velocidade média é dada por:
\(v_m = \frac{|\Delta {[H_2]}|}{\Delta t} = \frac{|\frac{0,8 - 0}{2}|}{10- 0} = \frac{0,4}{10} = 0,04\ \frac{mol}{L\cdot min}\)
Resposta Questão 6
Alternativa C.
A velocidade de consumo de nitrato de amônio nos 300 segundos iniciais é calculado da seguinte forma:
\(v_m = \frac{|(0,45 - 0,90)|}{300 - 0} = \frac{0,45}{300} = 0,0015\ \frac{mol}{L\cdot s}\)
Como o nitrato de amônio possui um coeficiente estequiométrico que é o triplo do coeficiente estequiométrico de NO2, então a velocidade de produção de NO2 nesse intervalo é equivalente a um terço da velocidade de consumo do nitrato de amônio.
Assim sendo:
\(v_m(NO_2) = \frac{v_m(NH_4NO_3)}{3} = \frac{0,0015}{3} = 0,0005 = 5\cdot 10^{-4}\ \frac{mol}{L\cdot s}\)
Resposta Questão 7
Alternativa C.
O coeficiente estequiométrico de H2 é o triplo de N2; logo, a velocidade de consumo de H2 é o triplo de N2. Assim, se a velocidade de N2 é de 6 mols/min, então a velocidade de consumo de H2 é igual a 18 mols/min.
Resposta Questão 8
Alternativa B.
Em 1 hora, 60 minutos, a concentração de H2O2 variou de 1,00 para 0,90 mol/L. Assim, a velocidade média em uma hora de experimento pode ser calculada:
\(v = \frac{|\Delta H_2O_2|}{\Delta t} = \frac{|0,90- 1,00|}{1 - 0} = \frac{0,10}{1} = 0,10\ \frac{mol}{L\ \cdot\ h}\)
Resposta Questão 9
Alternativa A.
Tanto o bicarbonato de sódio quanto o CO2 possuem o mesmo coeficiente estequiométrico; assim sendo, a velocidade de consumo de bicarbonato de sódio é numericamente igual à velocidade de produção de CO2, em mol/L.s. Sendo a massa molar do NaHCO3 igual a 84 g/mol, podemos dizer, então, que em cada pastilha há:
\(nº\ mols = \frac{massa}{Massa\ Molar}=\frac{504}{84}=6\ mols\)
A concentração de NaHCO3, em mol/L, é então:
\(M(NaHCO_3)=\frac{6 mol}{0,2 L}=30 \frac {mol}{L}\)
Por fim, a velocidade de consumo de bicarbonato de sódio, que é numericamente igual à velocidade de produção de CO2:
\(v = \frac{\Delta |[NaHCO_3]|}{\Delta t} = \frac{|0 - 30|}{1 - 0} = \frac{30}{1} = 30\ \frac{mol}{L\ \cdot\ s}\)
Resposta Questão 10
Alternativa C.
A velocidade média da reação química é dada pela velocidade média da substância dividida pelo seu coeficiente estequiométrico. Como a tabela foi dada em termos de gás oxigênio, a velocidade média da reação será calculada da seguinte forma:
\(v_m(reação)=\frac{v_m(O_2)}{\frac{1}{2}}\)
A velocidade média de consumo de gás oxigênio no intervalo de 1 a 4 minutos é dado pela expressão:
\(v_m(O_2) = \frac{\Delta|[O_2]|}{\Delta t} = \frac{|0,015 - 0,027|}{4 - 1} = \frac{0,012}{3} = 0,004\ \frac{mol}{L\ \cdot\ min}\)
Assim, a velocidade média da reação será:
\(v_m(reação)=\frac{0,004}{\frac{1}{2}}=0,008\frac{mol}{L\cdot min}\)
Resposta Questão 11
Alternativa D.
Ao se observar a reação balanceada, vê-se que o coeficiente de HN3 é o dobro do coeficiente estequiométrico de H2. Já o coeficiente estequiométrico de N2 é o triplo do coeficiente estequiométrico de H2, ou 1,5 vez maior que o coeficiente estequiométrico de HN3.
Dessa forma, pode-se dizer que:
\( v(H_2) = \frac{v(\text{HN}_3)}{2} = \frac{3,0 \cdot 10^{-3}}{2} = 1,5 \cdot 10^{-3} \, \text{mol/(L·min)} \)
\(v(N_2) = 1,5 \cdot v(\text{HN}_3) = 1,5 \cdot 3 \cdot 10^{-3} = 4,5 \cdot 10^{-3} \, \text{mol/(L·min)}\)
Resposta Questão 12
Alternativa E.
Se a velocidade média de consumo de butano é de 0,01 mol/min, então a velocidade média de produção de CO2 é igual a 4 vezes a velocidade média de consumo de butano, uma vez que o coeficiente estequiométrico do CO2 é 4 vezes maior que o coeficiente estequiométrico do C4H10. Assim, a velocidade média de produção de CO2 é igual a 0,04 mol/min. Em uma hora, que equivale a 60 minutos, o número de mols de CO2 produzido é igual a 0,04 x 60, que é igual a 2,4 mols.
Como a massa molar de CO2 é igual a 44 g/mol, então, nesse cozimento, foram produzidos 2,4 x 44 gramas de CO2, o que é igual a 105,6 gramas.



