Questão 1
(Uncisal) No filme De volta para o futuro (Universal Pictures, USA, 1985), o protagonista cria uma máquina do tempo utilizando um automóvel modelo DeLorean DMC 1981. Para isso, o seu motor foi modificado para que fosse capaz de produzir uma potência de 1,21 GW. Supondo o rendimento do motor de 50%, a massa do automóvel igual a 1210 Kg e desprezando a resistência do ar, um DeLorean com uma potência de 1,21 GW atingiria de 0 a 100 Km/h (\(100\ Km/h\ ↓≈\ 27\ m/s\)) em um tempo de:
A) 223,1 μs
B) 364,5 μs
C) 441,0 μs
D) 605,0 μs
E) 729,0 μs
Questão 2
(PUC) Em um período de muito frio, um casal utiliza em seu quarto um aquecedor elétrico de potência nominal 1200 W ligado a 110 V. Mesmo ligado a noite toda, possui um termostático que o desliga automaticamente por certo período de tempo. Pode-se dizer que permanece utilizando a potência elétrica nominal por 5 horas por dia. Sabendo que o custo do kWh é de R$ 0,40, durante o mês, qual seria o gasto com o aquecedor elétrico? (Considere que o valor do kWh seja o total, já incluso impostos e taxas).
A) 180 reais
B) 55 reais
C) 25 reais
D) 12 reais
E) 72 reais
Questão 3
(FCM) Em uma cachoeira aproveitada para mover uma roda d’água, a potência disponível é de 300 kW. Qual a potência útil para essa roda d’água cujo rendimento é de 50%?
A) 150 kW
B) 450 kW
C) 50 kW
D) 100 kW
E) 200 kW
Questão 4
(UFPR) O consumo elétrico de uma unidade residencial foi medido pelo seu proprietário, e o resultado obtido foi expresso pelo gráfico ao lado, que descreve o consumo de corrente elétrica (i) da residência ao longo das 24 horas do dia (t). A unidade residencial é alimentada por uma tensão de 110 V.
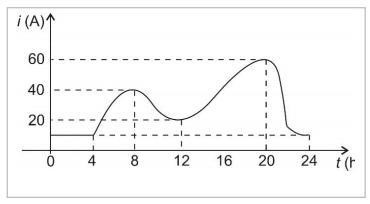
Considerando os dados expressos no gráfico, assinale a alternativa que apresenta corretamente o valor da maior potência elétrica consumida ao longo do dia.
A) 1,1 kW.
B) 2,2 kW.
C) 4,4 kW.
D) 6,6 kW.
E) 8,8 kW.
Questão 5
Analise as proposições abaixo e determine quais das alternativas correspondem a tipos de potência:
I. Potência mecânica.
II. Potência fraca.
III. Potência elétrica.
IV. Potência forte.
V. Potência instantânea.
Quais das alternativas apresentam as classificações de potência elétrica?
A) Alternativas I, II e III.
B) Alternativas I, IV e V.
C) Alternativas II, III e IV.
D) Alternativas II, IV e V.
E) Alternativas I, III e V.
Questão 6
Calcule a potência elétrica em um resistor elétrico de 48,4 Ω que foi conectado a um circuito elétrico que possui uma bateria de 220 V.
A) 700 W
B) 800 W
C) 900 W
D) 1000 W
E) 1100 W
Questão 7
Calcule a potência elétrica em um circuito que apresenta um resistor de 25 Ω que é percorrido por uma corrente de 6 A:
A) 700 W
B) 800 W
C) 900 W
D) 1000 W
E) 1100 W
Questão 8
Calcule a potência elétrica de um chuveiro elétrico que, ligado todos os dias por 15 minutos, consome uma energia elétrica mensal de 4 kWh.
A) 0,4 kW
B) 0,5 kW
C) 0,6 kW
D) 0,7 kW
E) 0,8 kW
Questão 9
Calcule a potência termodinâmica de um gás que sofre uma transformação isobárica com pressão de 3 Pa que varia seu volume em \(1000\ m^3\) durante 30 segundos.
A) 100 W
B) 200 W
C) 300 W
D) 400 W
E) 500 W
Questão 10
Calcule a potência de um resistor aquecido em razão do efeito Joule quando 450 J do seu calor é dissipado durante 30 minutos.
A) 4,7 W
B) 3,6 W
C) 2,5 W
D) 1,4 W
E) 0,3 W
Questão 11
Calcule a potência mecânica de uma pessoa de 100 kg que saiu do repouso e atingiu uma velocidade de 18 km/h em 15 minutos.
A) 1080 W
B) 83,4 W
C) 18 W
D) 1,4 W
E) 0,22 W
Questão 12
Quais proposições apresentam a unidade de medida correspondente à grandeza física estudada em potência?
I. A potência elétrica é medida em Ohm.
II. A potência instantânea é medida em Volt.
III. A potência mecânica é medida em Watt.
IV. A potência termodinâmica é medida em Ohm.
V. O trabalho é medido em Joule.
VI. A energia é medida em Joule.
A) Alternativas I, II e III.
B) Alternativas III, V e VI
C) Alternativas IV, V e VI.
D) Alternativas II, III e VI.
E) Alternativas I, III e V
Resposta Questão 1
Alternativa E
Calcularemos a variação de tempo por meio da fórmula que a relaciona à potência mecânica e ao trabalho:
\(P=\frac{W}{∆t}\)
Não foi informado o valor do trabalho, mas podemos obtê-lo usando o teorema do trabalho e da energia cinética, em que o trabalho realizado pelo motor do carro equivale à variação de energia cinética sofrida pelo carro:
\(W=∆E_c\)
\(W=E_{c\ final}-E_{c\ inicial}\)
\(W=\frac{m\cdot v_{final^2}}2-\frac{m\cdot v_{inicial^2}}2\)
\(W=\frac{1210\cdot27^2}2-\frac{1210\cdot0^2}2\)
\(W=\frac{1210\cdot27^2}{2-0}\)
\(W=441\ 045\ J\)
Por fim, substituiremos o valor do trabalho na equação da potência mecânica e o valor do rendimento do supercarro:
\(η\cdot P=\frac{W}{∆t}\)
\(50 \%\cdot1,21\ G=\frac{441\ 045}{∆t}\)
O G significa giga e vale \(10^9\), então:
\(50 \%\cdot1,21\ G=\frac{441\ 045}{∆t}\)
\(0,605\cdot10^9=\frac{441\ 045}{∆t}\)
\(∆t=\frac{441\ 045}{0,605\cdot10^9}\)
\(∆t=729\ 000\cdot10^{-9}\)
\(∆t=729\cdot10^3\cdot10^{-9}\)
\(∆t=729\cdot10^{-6}\)
\(∆t=729\ μs\)
Resposta Questão 2
Alternativa E
Primeiramente, calcularemos a quantidade de horas em que o aquecedor é usado em um mês de 30 dias:
\(5\ horas\ diárias\cdot 30\ dias=150\ horas\)
Então, calcularemos o consumo de energia elétrica usando a fórmula que o relaciona à potência elétrica e à variação de tempo:
\(P=\frac{E}{∆t}\)
\(1200=\frac{E}{150}\)
\(E=1200\cdot150\)
\(E=180\ 000\ Wh\)
\(E=180\ kWh\)
Por fim, multiplicaremos o valor da energia gasta pelo custo do kWh, então o custo final será de:
\(180\cdot R$\ 0,40=R$\ 72,00\)
Resposta Questão 3
Alternativa A
Calcularemos a potência elétrica útil por meio da fórmula que a relaciona ao rendimento e à potência elétrica total:
\(η=\frac{P_U}{P_T} \)
\(50 \%=\frac{P_U}{300}\)
\(\frac{50}{100}=\frac{P_U}{300}\)
\(P_U=\frac{50\cdot 300}{100}\)
\(P_U=150\ W\)
Resposta Questão 4
Alternativa D
Calcularemos a potência elétrica consumida durante o dia usando a fórmula que a relaciona à corrente elétrica e à tensão elétrica:
\(P=i\cdot ∆U\)
O maior valor de potência elétrica ocorrerá quando tivermos a intensidade da corrente elétrica máxima:
\(P=i_{máx}\cdot ∆U\)
\(P=60\cdot 110\)
\(P=6600\ W\)
\(P=6,6\ kW\)
Resposta Questão 5
Alternativa E
Os tipos de potência são elétrica, mecânica, instantânea e termodinâmica.
Resposta Questão 6
Alternativa D
Calcularemos a potência elétrica por meio da fórmula que a relaciona à tensão elétrica e à resistência elétrica:
\(P=\frac{U^2}R\)
\(P=\frac{220^2}{48,4}\)
\(P=\frac{48\ 400}{48,4}\)
\(P=1000\ W\)
Resposta Questão 7
Alternativa C
Calcularemos a potência elétrica usando a fórmula que a relaciona à resistência elétrica e à corrente elétrica:
\(P=R\cdot i^2\)
\(P=25\cdot6^2\)
\(P=25\cdot 36\)
\(P=900\ W\)
Resposta Questão 8
Alternativa B
Primeiramente, converteremos os minutos para hora:
\(\frac{15\ min}{60\ min}=0,25\ h\)
Então, em um mês de 30 dias, o chuveiro elétrico é usado por:
\(0,25\ h\cdot30\ dias=7,5\ h\)
Por fim, calcularemos a potência elétrica usando a fórmula que a relaciona à energia e à variação de tempo:
\(P=\frac{E}{∆t}\)
\(P=\frac{7,5}{15}\)
\(P=0,5\ kW\)
Resposta Questão 9
Alternativa A
Calcularemos a potência termodinâmica por meio da fórmula que a relaciona ao trabalho termodinâmico e à variação de tempo.
\(P=\frac{W}{∆t}\)
O trabalho termodinâmico pode ser dado pela fórmula:
\(W=p\cdot ∆V\)
Então, a potência termodinâmica é:
\(P=\frac{p\ \cdot∆V}{∆t}\)
\(P=\frac{3\cdot1000}{30}\)
\(P=\frac{3000}{30}\)
\(P=100\ W\)
Resposta Questão 10
Alternativa C
De início, converteremos o tempo de minutos para segundos:
\(30\ min×60=1800\ s\)
A potência desse resistor é calculada por meio da fórmula que a relaciona ao calor dissipado e à variação de tempo:
\(P=\frac{Q}{∆t}\)
\(P=\frac{450}{1800}\)
\(P=0,25\ W\)
Resposta Questão 11
Alternativa D
Primeiramente, converteremos a velocidade de km/h para m/s:
\(\frac{18\ km/h}{3,6}=5\ m/s\)
E converteremos o tempo de minutos para segundos:
\(15\ min×60=900\ s\)
Então, calcularemos a potência mecânica ocasionada pelo movimento da pessoa usando a fórmula que a relaciona ao trabalho e à variação de tempo:
\(P=\frac{W}{∆t}\)
O trabalho pode ser calculado pelo teorema do trabalho e da energia cinética:
\(P=\frac{∆E_c}{∆t}\)
\(P=\frac{E_{c\ final}-E_{c\ inicial}}{∆t}\)
\(P=\frac{\frac{m\cdot v_{final^2}}{2}-\frac{m\cdot v_{inicial^2}}{2}}{∆t}\)
\(P=\frac{\frac{100\cdot5^2}{2}-\frac{100\cdot0^2}{2}}{900}\)
\(P=\frac{\frac{100\cdot25}{2}-\ 0}{900}\)
\(P=\frac{1250}{900}\)
\(P=1,4\ W\)
Resposta Questão 12
Alternativa B
I. A potência elétrica é medida em Ohm. (falso)
A potência elétrica é medida em Watt.
II. A potência instantânea é medida em Volt. (falso)
A potência instantânea é medida em Watt.
III. A potência mecânica é medida em Watt. (verdadeiro)
IV. A potência termodinâmica é medida em Ohm. (falso)
A potência termodinâmica é medida em Watt.
V. O trabalho é medido em Joule. (verdadeiro)
VI. A energia é medida em Joule. (verdadeiro)



