Questão 1
(Enem) O eletrocardiograma é um exame cardíaco que mede a intensidade dos sinais elétricos advindos do coração. A imagem apresenta o resultado típico obtido em um paciente saudável e a intensidade do sinal (VEC) em função do tempo.
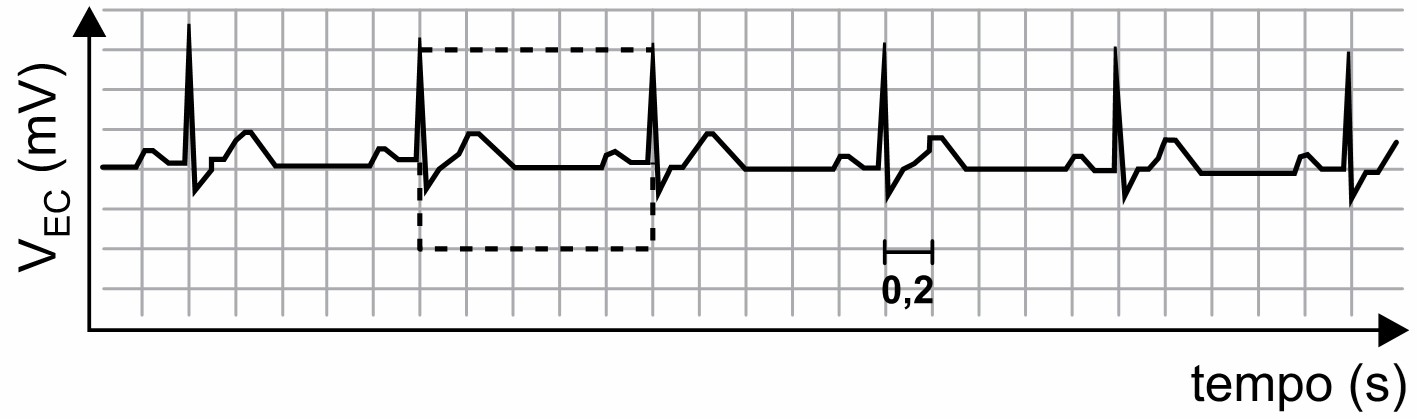
De acordo com o eletrocardiograma apresentado, qual foi número de batimentos cardíacos por minuto desse paciente durante o exame?
A) 30
B) 60
C) 100
D) 120
E) 180
Questão 2
(Enem) As notas musicais, assim como a grande maioria dos sons encontrados na natureza, são complexas e formadas pela superposição de várias ondas senoidais. A figura apresenta três componentes harmônicas e a composição resultante, construídas na mesma escala, para um instrumento sonoro. Essa composição carrega uma “assinatura sônica” ou timbre do corpo que a produz.
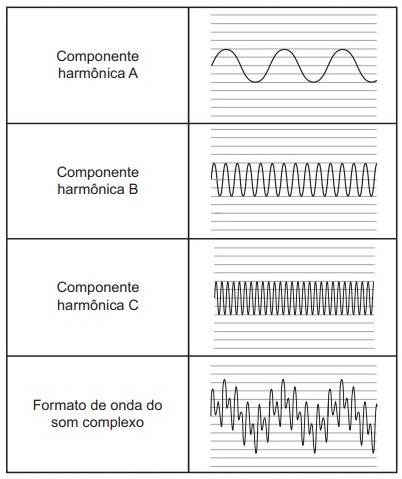
RODRIGUES, F. V. Fisiologia da música: uma abordagem comparativa (Revisão). (Revista da Biologia, v. 2, jun. 2008. Disponível em: www.ib.usp.br. Acesso em: 22 jun. 2012 (adaptado).
Essas componentes harmônicas apresentam iguais
A) amplitude e velocidade.
B) amplitude e frequência.
C) frequência e velocidade.
D) amplitude e comprimento de onda.
E) frequência e comprimento de onda.
Questão 3
(PUC) O gráfico a seguir representa a forma de uma onda com frequência constante.
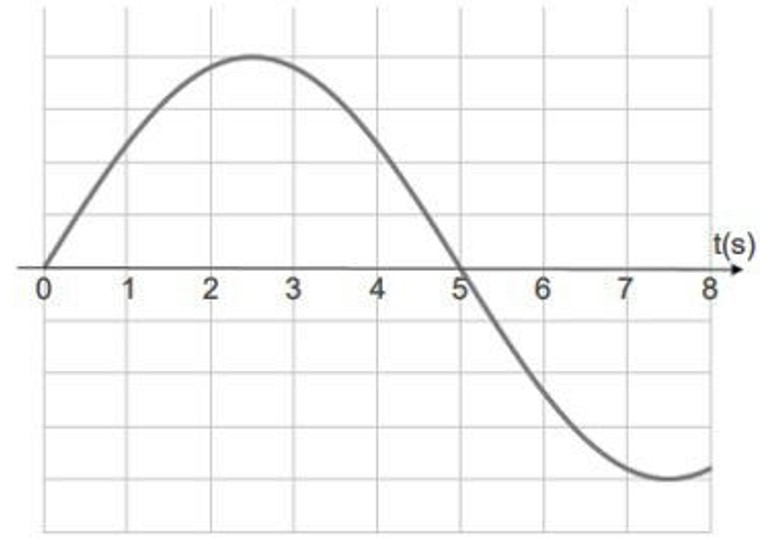
Sendo o comprimento de onda igual a 20 m, o período e a velocidade de propagação da onda valem, respectivamente, _______ e _______.
A) 10s – 1,0 m/s
B) 10s – 2,0 m/s
C) 20s – 1,0 m/s
D) 20s – 2,0 m/s
Questão 4
Uma onda períodica se propaga no vácuo com uma velocidade de 2 ∙ 108 m/s e frequência de 4 ∙ 105 Hz
e frequência de 4 ∙ 105 Hz . Com base nessas informações, calcule o comprimento de onda dessa onda.
. Com base nessas informações, calcule o comprimento de onda dessa onda.
A) 1 ∙ 103 m
B) 2 ∙ 104 m
C) 3 ∙ 105 m
D) 4 ∙ 106 m
E) 5 ∙ 107 m
Questão 5
Qual a velocidade de propagação de uma onda períodica com comprimento de onda igual a 10-10 m e período de 100s?
e período de 100s?
A) 108 m/s
B) 1012 m/s
C) 1010 m/s
D) 10-12 m/s
E) 10-8 m/s
Questão 6
De acordo com as características das ondas períodicas sonoras, elas não podem ser:
A) mecânicas.
B) eletromagnéticas.
C) tridimensionais
D) longitudinais.
E) senoidais.
Questão 7
As ondas períodicas que apresentam os formatos abaixo são chamadas de:
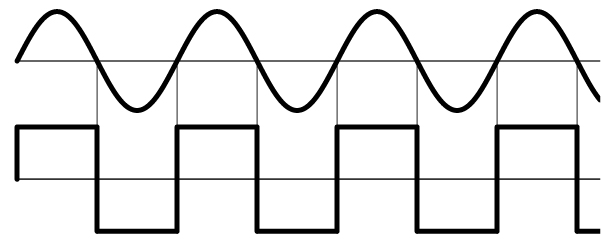
A) Senoidais.
B) Quadrangulares.
C) Triangulares.
D) Quadrangulares e triangulares.
E) Senoidais e quadrangulares.
Questão 8
As ondas períodicas não são classificadas quanto a:
A) natureza.
B) velocidade.
C) direção de vibração.
D) número de dimensões da propagação da sua energia.
Questão 9
Uma onda períodica possui uma frequência de oscilação de 500 Hz. Qual é o seu período?
A) 0,002s
B) 0,003s
C) 0,004s
D) 0,005s
E) 0,006s
Questão 10
Qual a velocidade de propagação de uma onda períodica que tem 2m de comprimento de onda e frequência de 100 Hz?
A) 50 m/s
B) 100 m/s
C) 150 m/s
D) 200 m/s
E) 250 m/s
Questão 11
Calcule a frequência de oscilação de uma onda períodica, sabendo que o seu período é de 0,5 segundo.
A) 0,3 Hz
B) 0,5 Hz
C) 1,0 Hz
D) 1,5 Hz
E) 2,0 Hz
Questão 12
Quais das alternativas apresentam as unidades de medidas correspondentes às grandezas físicas estudadas em ondas períodicas?
I. O período é medido em segundos.
II. A frequência é medida em segundos.
III. A velocidade de propagação da onda é medida em metros por segundo ao quadrado.
IV. O comprimento de onda é medido em metros quadrados.
V. O tempo é medido em segundos.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e V.
D) Alternativas II e III.
E) Alternativas II e IV.
Resposta Questão 1
Alternativa B.
Observando o gráfico é possível verificar que o período dos batimentos cardíacos é dado por 5 quadrados, cada um com 0,2 segundos, então:
\(T = 5 \cdot 0,2 = 1 \, \text{s} \)
Depois transformaremos os segundos para minutos, já que os batimentos cardíacos são dados em batimentos por minuto:
\(1 \, \text{s} = \frac{1}{60} \, \text{min} \)
Por fim, calcularemos o número de batimentos cardíacos em 1 minuto através da fórmula do período de oscilação:
\(T = \frac{\Delta t}{N} \)
\(\frac{1}{60} = \frac{1}{N} \)
\(N = 60 \, \text{batimentos} \)
Resposta Questão 2
Alternativa A.
Essas componentes harmônicas possuem a mesma amplitude, medida do eixo até a crista ou vale, e velocidade, que só varia com o meio em que a onda está se propagando.
Resposta Questão 3
Alternativa B.
O período será 10s, já que metade da onda demorou 5s, e calcularemos a velocidade de propagação da onda períodica através da sua fórmula, que a relaciona ao comprimento de onda e ao período:
\(v = \frac{\lambda}{T} \)
\(v = \frac{20}{10} \)
\(v=2 m/s\)
Resposta Questão 4
Alternativa E.
Calcularemos o comprimento de onda da onda períodica através da fórmula da velocidade de propagação da onda:
\(v = \lambda \cdot f \)
\(2 \cdot 10^8 = \lambda \cdot 4 \cdot 10^5 \)
\(\lambda = \frac{2 \ \cdot \ 10^8}{4 \ \cdot \ 10^5} \)
\(\lambda = 0,5 \cdot 10^{8 - 5} \)
\(\lambda = 0,5 \cdot 10^3 \)
\(\lambda = 5 \cdot 10^2 \, \text{m}\)
Resposta Questão 5
Alternativa D.
Calcularemos a velocidade de propagação da onda períodica a partir da fórmula que a relaciona ao comprimento de onda e ao período:
\(v = \frac{\lambda}{T}\)
\(v = \frac{10^{-10}}{100} \)
\(v = \frac{10^{-10}}{10^2} \)
\(v = 10^{-10 - 2} \)
\(v = 10^{-12} \, \text{m/s} \)
Resposta Questão 6
Alternativa B.
As ondas períodicas sonoras não são eletromagnéticas, já que precisam de um meio para se propagarem.
Resposta Questão 7
Alternativa E.
A primeira onda é chamada de senoidal, já que é descrita em termos da função seno, e a segunda onda é chamada de quadrangular, devido ao seu formato de quadrado.
Resposta Questão 8
Alternativa B.
Podemos classificar as ondas quanto a sua natureza, quanto a sua direção de vibração e quanto ao número de dimensões da propagação da sua energia.
Resposta Questão 9
Alternativa A.
Calcularemos o período da onda períodica através da fórmula:
\(T = \frac{1}{f} \)
\(T = \frac{1}{500} \)
\(T=0,002 s\)
Resposta Questão 10
Alternativa D.
Calcularemos a velocidade de propagação períodica através da fórmula:
\(v = \lambda \cdot f \)
\(v=2 \cdot 100\)
\(v=200 m/s\)
Resposta Questão 11
Alternativa E.
Calcularemos a frequência de oscilação da onda períodica através da fórmula:
\(f = \frac{1}{T} \)
\(f = \frac{1}{0,5} \)
\(f=2 Hz\)
Resposta Questão 12
Alternativa C.
I. O período é medido em segundos. (correta)
II. A frequência é medida em segundos. (incorreta)
A frequência é medida em Hertz.
III. A velocidade de propagação da onda é medida em metros por segundo ao quadrado. (incorreta)
A velocidade de propagação da onda é medida em metros por segundo.
IV. O comprimento de onda é medido em metros quadrados. (incorreta)
O comprimento de onda é medido em metros.
V. O tempo é medido em segundos. (correta)



