Questão 1
Uma quantia foi dividida entre três amigos: Heitor, Diego e Rafael. Heitor recebeu um quarto do total, enquanto Diego recebeu três oitavos do total. Qual fração do total coube a Rafael?
A) \(\frac{5}{8} \)
B) \(\frac{7}{8} \)
C) \(\frac{3}{8} \)
D) \(\frac{3}{4} \)
E) \(\frac{5}{16}\)
Questão 2
Em um campeonato de xadrez escolar, 90 estudantes participaram das partidas. Desses, 1/3 venceu mais de 10 partidas, 2/5 venceram entre 5 e 10 partidas, e o restante venceu menos de 5 partidas. Sabendo que o critério para se classificar para a fase regional era vencer, pelo menos, 5 partidas, quantos estudantes não se classificaram?
A) 18
B) 24
C) 30
D) 36
E) 42
Questão 3
Uma herança será dividida entre 3 irmãos. Carlos ficará com \(\frac {2}{5}\) a herança, e Luiza ficará com \(\frac {1}{4}\). O restante da herança será para Sofia. Qual fração da herança Sofia receberá?
A) \(\frac{7}{20}\)
B) \(\frac{3}{10} \)
C) \(\frac{1}{20} \)
D) \(\frac {9}{20}\)
E) \(\frac{5}{20} \)
Questão 4
No ano de 2024, o salário de Kárita foi de R$ 3500 por mês. Sabendo que ela sempre guarda a quinta parte para a sua reserva de emergência, qual será o valor guardado por ela ao final do ano?
A) R$ 2100
B) R$ 3600
C) R$ 5400
D) R$ 7000
E) R$ 8400
Questão 5
Em uma escola, o professor de Matemática percebeu que \(\frac {5}{8}\) da turma obtiveram notas superiores à média na última avaliação. Sabendo que havia 40 estudantes nesse exame, o número de estudantes que tiraram nota abaixo da média foi de:
A) 15 estudantes
B) 20 estudantes
C) 30 estudantes
D) 35 estudantes
E) 40 estudantes
Questão 6
Em uma escola, há 1800 alunos e 36 professores. A razão entre o número de alunos e o número de professores é igual a:
A) 1 professor para cada 36 alunos.
B) 36 professores para cada 50 alunos.
C) 50 alunos para cada professor.
D) 1 professor para cada 50 alunos.
E) 1 professor para cada 60 alunos.
Questão 7
Lucas comprou uma bicicleta com um valor total de R$ 1400. No primeiro mês, ele pagou 3/7 do valor da bicicleta e, no segundo mês, pagou 2/5 do valor do pagamento feito no primeiro mês. Qual fração do valor total da bicicleta ainda falta pagar?
A) 14/35
B) 21/35
C) 28/35
D) 36/35
E) 7/35
Questão 8
Sobre a adição e a subtração de frações, julgue as afirmativas a seguir:
I. Quando somamos frações com denominadores iguais, somamos apenas os numeradores e mantemos o denominador.
II. Quando os denominadores são diferentes, é necessário encontrar o mínimo múltiplo comum (MMC) entre os denominadores antes de somá-los ou subtraí-los.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Ambas as afirmativas são verdadeiras.
D) Ambas as afirmativas são falsas.
Questão 9
(Enem PPL) A fim de reforçar o orçamento familiar, uma dona de casa começou a produzir doces para revender. Cada receita é composta de 4/5 de quilograma de amendoim e 1/5 de quilograma de açúcar.
O quilograma de amendoim custa R$ 10,00 e o do açúcar, R$ 2,00. Porém, o açúcar teve um aumento e o quilograma passou a custar R$ 2,20. Para manter o mesmo custo com a produção de uma receita, essa dona de casa terá que negociar um desconto com o fornecedor de amendoim.
Nas condições estabelecidas, o novo valor do quilograma de amendoim deverá ser igual a
A) R$ 9,20.
B) R$ 9,75.
C) R$ 9,80.
D) R$ 9,84.
E) R$ 9,95.
Questão 10
(Enem) Foi feita uma pesquisa sobre a escolaridade dos funcionários de uma empresa. Verificou-se que 1/4 dos homens que ali trabalham têm o ensino médio completo, enquanto 2/3 das mulheres que trabalham na empresa têm o ensino médio completo. Constatou-se, também, que entre todos os que têm o ensino médio completo, metade são homens.
A fração que representa o número de funcionários homens em relação ao total de funcionários dessa empresa é:
A) 1/8
B) 3/11
C) 11/24
D) 2/3
E) 8/11
Questão 11
(Enem) Em um certo teatro, as poltronas são divididas em setores. A figura apresenta a vista do setor 3 desse teatro, no qual as cadeiras escuras estão reservadas e as claras não foram vendidas.
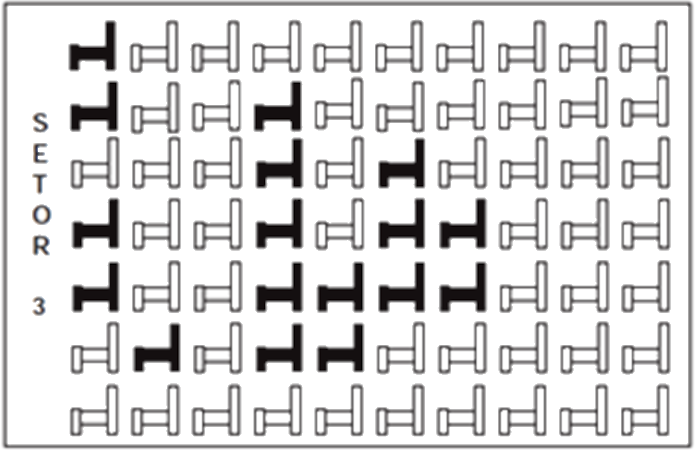
A razão que representa a quantidade de cadeiras reservadas do setor 3 em relação ao total de cadeiras desse mesmo setor é:
A) 17/70
B) 17/53
C) 53/70
D) 53/17
E) 70/17
Questão 12
(Enem) No contexto da matemática recreativa, utilizando diversos materiais didáticos para motivar seus alunos, uma professora organizou um jogo com um tipo de baralho modificado. No início do jogo, vira-se uma carta do baralho na mesa e cada jogador recebe em mãos nove cartas. Deseja-se formar pares de cartas, sendo a primeira carta a da mesa e a segunda, uma carta na mão do jogador, que tenha um valor equivalente àquele descrito na carta da mesa. O objetivo do jogo é verificar qual jogador consegue o maior número de pares. Iniciado o jogo, a carta virada na mesa e as cartas da mão de um jogador são como no esquema:
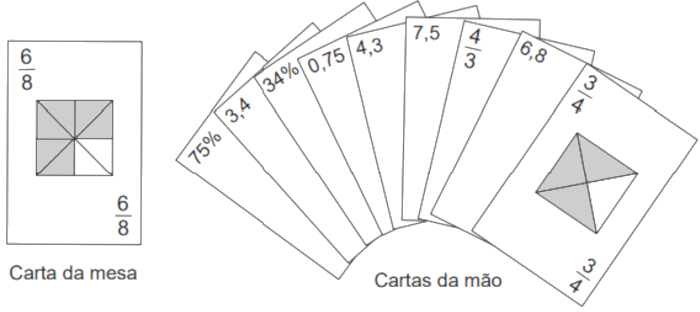
Segundo as regras do jogo, quantas cartas da mão desse jogador podem formar um par com a carta da mesa?
A) 9
B) 7
C) 5
D) 4
E) 3
Resposta Questão 1
Alternativa C
Sabemos que Heitor recebeu \(\frac {1}{4}\) e que Diego recebeu \(\frac {3}{8}\), então temos que:
\(\frac{1}{4} + \frac{3}{8} \)
Para realizar a soma, é necessário encontrar um múltiplo em comum a 4 e 8, que, no caso, é o próprio 8, então temos que:
\(\frac{2}{8} + \frac{3}{8} = \frac{5}{8} \)
Agora sabemos que 58 da quantia está com Heitor e Diego, então resta para Rafael um total de:
\(1 - \frac{5}{8} \)
\(\frac{8}{8} - \frac{5}{8} \)
\(\frac{3}{8} \)
Resposta Questão 2
Alternativa B.
Sabemos que \(\frac {1}{3}\) dos estudantes venceu mais de 10 partidas, então temos que:
\(\frac{1}{3} \cdot 90 = \frac{90}{3} = 30 \text{ estudantes} \)
Sabemos também que \(\frac {2}{5}\) conseguiram entre 10 e 5 vitórias:
\(\frac{2}{5} \cdot 90 = \frac{180}{5} = 36 \text{ estudantes}\)
O restante dos estudantes venceu menos de 5 partidas:
90 - 30 - 36
90 - 66
24
Então 24 estudantes não se classificaram.
Resposta Questão 3
Alternativa A.
Primeiro calcularemos a soma entre a parte do Carlos e da Luiza:
\(\frac{2}{5} + \frac{1}{4} \)
O mínimo múltiplo comum (MMC) entre 5 e 4 é igual a 20, logo, temos que:
\(\frac{8}{20} + \frac{5}{20} = \frac{13}{20} \)
Para calcular o que restou dessa herança, temos que:
\(1 - \frac{13}{20} \)
\(\frac{20}{20} - \frac{13}{20} = \frac{7}{20} \)
Resposta Questão 4
Alternativa E.
Primeiro calcularemos \(\frac {1}{5}\) de 3500.
\(3500 \cdot \frac{1}{5} = \frac{3500}{5} = 700 \)
Se a cada mês ela guarda 700 reais, então, após um ano, o valor guardado será de:
\(700 \cdot 12 = 8400 \)
Resposta Questão 5
Alternativa A.
Se \(\frac {5}{8}\) dos estudantes tiraram nota acima da média, então, para encontrar a fração que representa a quantidade de estudantes que tiraram nota abaixo da média, temos que:
\(1 - \frac{5}{8} = \frac{8}{8} - \frac{5}{8} = \frac{3}{8} \)
Agora, basta calcular \(\frac{3}{8} \) de 40.
\(\frac{3}{8} \cdot 40 = \frac{120}{8} = 15 \text{ estudantes}\)
Resposta Questão 6
Alternativa D.
Sabemos que há 36 professores e 1800 estudantes, então, montando a fração, temos que:
\(\frac{36}{1800}\)
Note que é possível simplificar essa fração dividindo por 36 tanto no numerador quanto no denominador:
\(\frac{36^{36}}{1800^{36}} = \frac{1}{50}\)
Então há 1 professor para cada 50 alunos.
Resposta Questão 7
Alternativa A.
\(\frac{3}{7} + \frac{2}{5} \cdot \frac{3}{7} = \frac{15 + 6}{35} = \frac{21}{35} \)
Para calcular a fração que representa o que falta pagar da bicicleta, temos que 35 – 21 = 14, então esse valor pode ser representado pela fração \(\frac {14}{35}\).
Resposta Questão 8
Alternativa C.
I. Quando somamos frações com denominadores iguais, somamos apenas os numeradores e mantemos o denominador. (correta)
Quando os denominadores são iguais, basta somar os numeradores e manter o denominador igual.
II. Quando os denominadores são diferentes, é necessário encontrar o mínimo múltiplo comum (MMC) entre os denominadores antes de somá-los ou subtraí-los. (correta)
Para somar ou subtrair frações com denominadores diferentes, é preciso primeiro igualá-los, e um dos métodos para isso é calcular o MMC entre os denominadores.
Resposta Questão 9
Alternativa E.
A receita é composta de:
- \(\frac{4}{5} \) kg de amendoim, que custa R$ 10 o kg.
- \(\frac{1}{5} \) de açúcar, que custa R$ 2 o kg.
O custo total será de:
\(10 \cdot \frac{4}{5} + 2 \cdot \frac{1}{5} = 8 + 0,4 = 8,40 \)
Como já sabemos que o custo do açúcar é agora R$ 0,44, devemos fazer com que o custo do amendoim seja tal que a receita continue custando R$ 8,40.
Ou seja, o custo do amendoim deve ser:
8,40 - 0,44 = 7,96 reais
Sabemos que o custo de \(\frac{4}{5} \) kg de amendoim deve ser igual a 7,96:
\(7,96 \div \frac{4}{5} = 7,96 \cdot \frac{5}{4} = 9,95 \)
Então o novo valor do kg do amendoim deve ser 9,95.
Resposta Questão 10
Alternativa E.
Dados:
- x: mulher
- y: homem
Sabemos que:
\(({\frac{1}{4}y + \frac{2}{3}x}) \div {2} = \frac{y}{4} \)
Então temos que:
\(\frac{1}{4}y + \frac{2}{3}x = \frac{y}{2} \)
\(\frac{2}{3}x = \frac{y}{2} - \frac{y}{4} \)
\(\frac{2}{3}x = \frac{2y - y}{4} \)
\(\frac{2}{3}x = \frac{y}{4}
\)
\(2 \cdot 4 x = 3y\)
\( 8x = 3y\)
\(x = \frac{3}{8}y \)
Queremos encontrar a razão entre o número de homens e o número total de funcionários. Sabemos que o número total de funcionários é a soma y + x, então temos que:
\(\frac{y}{y + x}\)
Substituindo x pelo valor encontrado anteriormente, temos que:
\(\frac{y}{y + \frac{3}{8}y} \)
\(\frac{y}{\frac{8y + 3y}{8}} \)
\(\frac{y}{\frac{11y}{8}} \)
\(y \cdot \frac{8}{11y} \)
\(\frac{8}{11} \)
Resposta Questão 11
Alternativa A.
Há 17 cadeiras ocupadas entre as 70 cadeiras do setor, logo, a fração desejada é 17/70.
Resposta Questão 12
Alternativa E.
A carta da messa é a fração \(\frac{6}{8} \), que é equivalente a \(\frac{3}{4} \) e 0,75.
Quando analisamos as cartas da mão, temos que:
\(75\% = 0,75 = \frac{3}{4} \)
Então há 3 cartas da mão que podem formar um par com a carta da mesa.



