Exercícios sobre volume do cone

Um cone possui altura medindo 5 cm e diâmetro da base igual a 8 cm. Considerando π = 3, o volume desse cone é igual a:

A) 40 cm³

B) 50 cm³

C) 60 cm³

D) 80 cm³

E) 100 cm³

Um cone possui volume igual a 100 π cm³. Sabendo que o seu raio mede 5 cm, então a medida da sua altura é igual a:

A) 6 cm

B) 8 cm

C) 10 cm

D) 12 cm

E) 14 cm

Qual é a medida do raio de um cone, em metros, que possui altura igual a 6 m e volume igual a 155 m³, utilizando π = 3,1?

A) 4

B) 5

C) 6

D) 7

E) 8

Um determinado cilindro possui altura medindo x cm e raio da base medindo y cm. Para encher esse cilindro de areia, foi utilizado um cone de mesma altura e mesma base. Se o cone estiver cheio até o limite do seu volume, qual é o número de vezes que é preciso para preencher o cone e despejar no cilindro para que este fique totalmente cheio?

A) 2 vezes

B) 3 vezes

C) 4 vezes

D) 5 vezes

E) 6 vezes

Um reservatório cônico será construído para armazenagem de gás de uma determinada indústria. Sabendo que esse reservatório vai ter 3,5 metros de altura e 3,0 metros de diâmetro, então o volume máximo desse reservatório é de:

A) $2,625π\ m^3$

B) $5,250π\ m^3$

C) $7,875π\ m^3$

D) $11,812π\ m^3$

E) $15,750π\ m^3$

O reservatório de gás de um laboratório possui formato de um cilindro, com 12 m³ de volume. Devido ao grande desgaste desse reservatório, durante a manutenção decidiram substituir esse reservatório por um cone, com mesma altura e mesmo raio da base que o reservatório anterior. Nessas condições, o volume do novo reservatório será de:

A) 36 m³

B) 12 m³

C) 8 m³

D) 6 m³

E) 4 m³

Em um reservatório no formato de um cone cabem 33490 litros. Se esse reservatório possui 8 metros de profundidade, considerando π = 3,14, então o diâmetro desse reservatório deve ser de, aproximadamente:

A) 4 metros

B) 3 metros

C) 2 metros

D) 1 metro

E) 0,5 metro

Uma empresa de perfume resolveu mudar o formato do recipiente dos seus perfumes. Antes, a embalagem possuía formato de um paralelepípedo retângulo, com 10 cm de altura, 8 cm de comprimento e 2,8 cm de largura. Se agora essa embalagem for formada por um cone com 10 cm de altura e 8 cm de raio, então a diferença entre o volume da embalagem anterior e o da nova embalagem é de:

A) 384 cm³

B) 224 cm³

C) 160 cm³

D) 64 cm³

E) 52 cm³

Analise o cone a seguir:

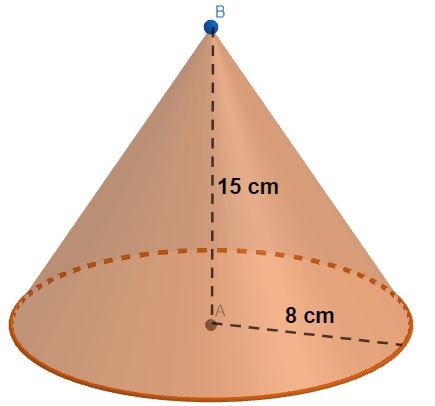
O volume do cone em centímetros cúbicos é de:

A) 180 π

B) 240 π

C) 250 π

D) 280 π

E) 320 π

Um recipiente possui formato de um cone, como o da imagem a seguir:

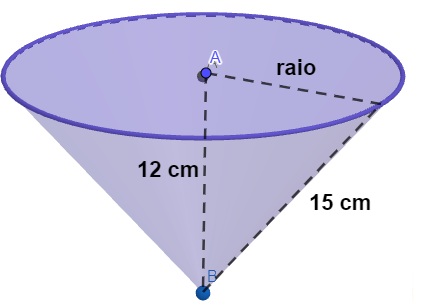
Podemos afirmar que a medida do volume desse recipiente é de:

(Use π = 3.)

A) 243 cm³

B) 324 cm³

C) 486 cm³

D) 972 cm³

E) 1080 cm³

(Enem) Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes. Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual.

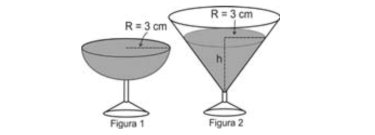
Considere:

$V_{esfera}= \frac{4}3 πR^3\ \ e \ \ V_{cone}= \frac{1}3 πR^2 h$

Sabendo que a taça com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taça, em centímetros, é de

A) 1,33

B) 6,00

C) 12,00

D) 56,52

E) 113,04

(Enem) Em regiões agrícolas, é comum a presença de silos para armazenamento e secagem da produção de grãos, no formato de um cilindro reto, sobreposto por um cone, e dimensões indicadas na figura. O silo fica cheio e o transporte dos grãos é feito em caminhões de carga cuja capacidade é de 20 m³. Uma região possui um silo cheio e apenas um caminhão para transportar os grãos para a usina de beneficiamento.

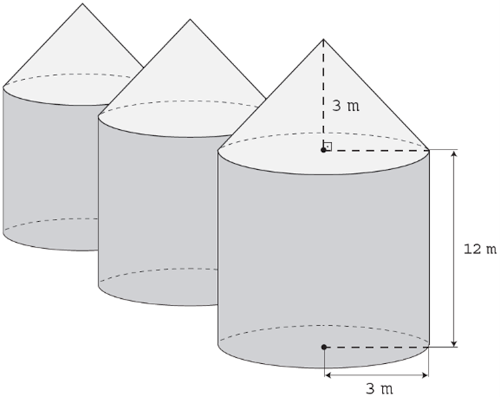
Utilize 3 como aproximação para π.

O número mínimo de viagens que o caminhão precisará fazer para transportar todo o volume de grãos armazenados no silo é

A) 6

B) 16

C) 17

D) 18

E) 21