Questão 1
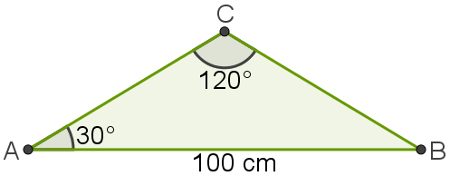
Um triângulo ABC possui os ângulos A = 30° e C = 120°. Além disso, o lado AB desse triângulo mede 100 cm. Qual é a medida do lado AC? (Considere √3 = 1,7).
a) 56,6 cm
b) 66,6 cm
c) 76,6 cm
d) 86,6 cm
e) 96,6 cm
Questão 2
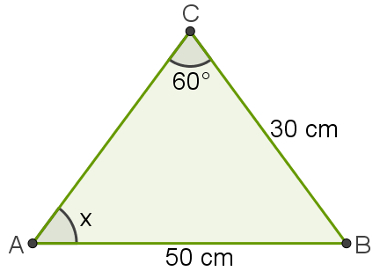
O triângulo ABC, na imagem abaixo, possui o lado AB = 50 cm e o lado CB = 30 cm. Sabendo que o ângulo C = 60°, qual é o seno do ângulo A? (considere √3 = 1,7 e sen31° = 0,51).
a) 30°
b) 31°
c) 32°
d) 33°
e) 34°
Questão 3
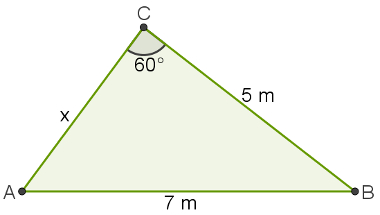
Qual o comprimento do lado AC do triângulo a seguir, sabendo que o ângulo C mede 60°, o lado oposto a ele mede 7 metros e o outro lado mede 5 metros.
a) 1 metro
b) 2 metros
c) 3 metros
d) 5 metros
c) 8 metros
Questão 4
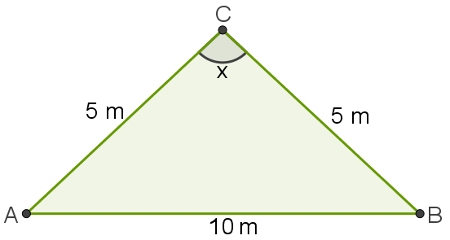
Calcule o cosseno do ângulo C no triângulo abaixo com base em suas medidas expostas na figura.
a) 1
b) – 1
c) 2
d) – 2
e) 3
Resposta Questão 1
Observe que conhecemos a medida de dois ângulos e de um lado desse triângulo. Como queremos saber a medida de um segundo lado, podemos usar a lei dos senos. O lado que mede 100 cm é oposto ao ângulo de 120°. Já o lado AC é oposto ao ângulo B, que não possui medida. Usando a soma dos ângulos internos de um triângulo, temos:
A + B + C = 180°
30° + 120° + C = 180°
150° + C = 180°
C = 180° – 150°
C = 30°
Seja AC = x, pela lei dos senos, teremos:
x = 100
sen30° sen120°
Sabendo que sen120° = sen(180° – 120°) = sen60°, teremos:
x = 100
sen30° sen60°
x·sen60° = 100·sen30°
x·√3 = 100·1
2 2
x·√3 = 100
x = 100
√3
Racionalizando:
x = 100√3
√3√3
x = 100√3
3
x = 100·1,7
3
x = 170
3
x = 56,6 cm
Gabarito: Alternativa A
Resposta Questão 2
Seja  = x, o seno do ângulo  pode ser calculado usando a lei dos senos:
30 = 50
senx sen60°
50·senx = 30·sen60°
50·senx = 30·√3
2
50·senx = 15·√3
senx = 15·√3
50
senx = 3·√3
10
senx = 3·1,7
10
senx = 5,1
10
senx = 0,51
Como sen31° = 0,51, então:
x = 31°
Gabarito: Alternativa B
Resposta Questão 3
Para resolver esse problema, basta usar a lei dos cossenos:
72 = 52 + x2 – 2·5·x·cos60°
49 = 25 + x2 – 10x·1/2
49 – 25 = x2 – 5x
24 = x2 – 5x
x2 – 5x – 24 = 0
Usando o método de completar quadrados, observe que metade de b = – 2,5 e que 2,52 = 6,25. Assim:
x2 – 5x – 24 + 6,25 = 0 + 6,25
x2 – 5x + 6,25 = 6,25 + 24
√(x – 2,5)2 = √30,25
x – 2,5 = ± 5,5
x = ± 5,5 + 2,5
x’ = 5,5 + 2,5 = 8
x’’ = – 5,5 + 2,5 = – 3
Como o resultado negativo não pode representar uma medida de comprimento, então a medida do lado AC é igual a 8 metros.
Gabarito: Alternativa E
Resposta Questão 4
Para resolver esse problema, basta usar a lei dos cossenos:
102 = 52 + 52 – 2·5·5·cosx
100 = 25 + 25 – 50·cosx
100 – 25 – 25 = – 50·cosx
50 = – 50·cosx
50 = cosx
– 50
cosx = – 1
Gabarito: Alternativa B