Questão 1
Analise o triângulo a seguir:
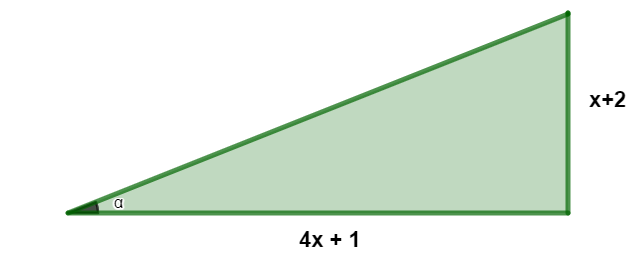
Sabendo que a tangente do ângulo α é igual a 12, então o valor de x é:
A) \(\frac{3}{2}\)
B) \(\frac{2}{3}\)
C) \(\frac{1}{2}\)
D) \( 2\)
E) \(\frac{3}{4}\)
Questão 2
Analisando o triângulo retângulo a seguir, podemos afirmar que a tangente do ângulo α é igual a:
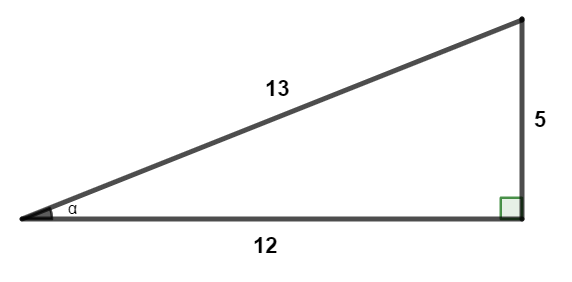
A) \(\frac{5}{13}\)
B) \(\frac{5}{12}\)
C) \(\frac{12}{13}\)
D) \( \frac{13}{12}\)
E) \(\frac{12}{5}\)
Questão 3
Na arquitetura é muito comum a representação de figuras geométricas para projetar construções. Durante os seus estudos na arquitetura, Kárita precisou desenhar uma reta tangente a um círculo. A reta é tangente a um círculo quando:
A) passa pelo centro desse círculo.
B) intercepta a circunferência em dois pontos.
C) intercepta a circunferência em um único ponto.
D) não intercepta a circunferência.
Questão 4
Na imagem a seguir temos duas circunferências, uma menor, de centro C, e outra maior, de centro A. Podemos observar que essas circunferências se encontram no ponto B.
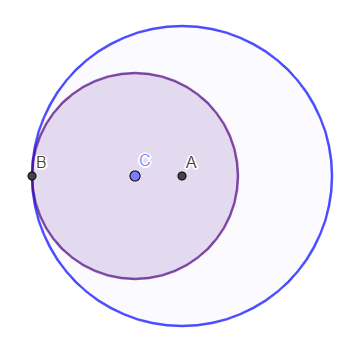
Após analisar a imagem, julgue as afirmativas a seguir:
I. A circunferência A é tangente interna à circunferência C.
II. O ponto de tangência dessas circunferências é o ponto B.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira
B) Somente a afirmativa II é verdadeira
C) Ambas as afirmativas são verdadeiras
D) Ambas as afirmativas são falsas.
Questão 5
Em um triângulo retângulo, a tangente de um dos seus ângulos agudos é igual a 1. Nesse sentido, podemos afirmar que:
A) Esse triângulo é retângulo e equilátero.
B) Esse triângulo é retângulo e isósceles.
C) Esse triângulo é retângulo e escaleno.
D) Esse triângulo é retângulo e obtusângulo.
E) Esse triângulo não é retângulo.
Questão 6
Dado um triângulo retângulo de catetos medindo a e b, observou-se que a razão entre os catetos a e b é igual a \(\sqrt3\). Nessas condições, podemos afirmar que a medida do ângulo oposto ao lado de medida b é igual a:
A) 30º
B) 45º
C) 60º
D) 75º
E) 90º
Questão 7
Determinado ângulo possui seno igual a \( \frac{2}{3}\) e cosseno igual a \(\frac{\sqrt5}{3}\), então o valor da tangente desse ângulo é:
A) \( \frac{2\sqrt5}{5}\)
B) \( \sqrt5\)
C) \( \frac{\sqrt5}{2}\)
D) \( \frac{1}{2}\)
E) \( \frac{1}{5}\)
Questão 8
A área de lazer de um condomínio possui formato de um triângulo retângulo, com as medidas como do esboço a seguir:
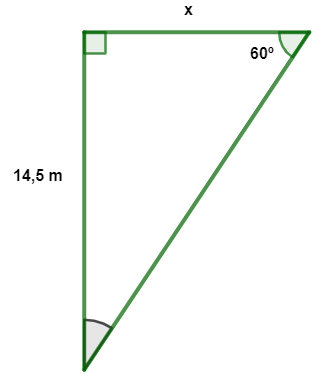
Analisando essa região, podemos afirmar que a área de lazer desse condomínio possui: (use √3 = 1,7)
A) 8,25 m²
B) 18,520 m²
C) 30,812 m²
D) 61,625 m²
E) 123,250 m²
Questão 9
Analisando o retângulo a seguir, e utilizando \( \frac{\sqrt3}{3}=0,58\), o perímetro do terreno demonstrado é:
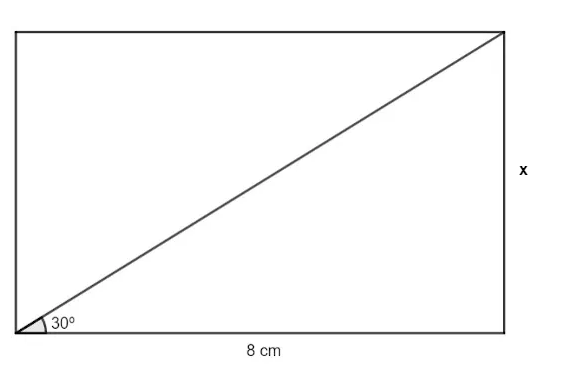
A) 4,64 cm
B) 12,64 cm
C) 20,20 cm
D) 23,42 cm
E) 25,28 cm
Questão 10
Um ângulo possui tangente medindo 0,3443 e seno medindo 0,3256, então o valor do cosseno desse ângulo é de aproximadamente:
A) 0,3349
B) 0,4728
C) 0,6699
D) 0,9457
E) 1,0574
Questão 11
(Enem) Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular de 3 km x 2 km que contém uma área de extração de ouro delimitada por um quarto de círculo de raio 1 km a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro, os irmãos acordaram em repartir a propriedade de modo que cada um ficasse com a terça parte da área de extração, conforme mostra a figura.
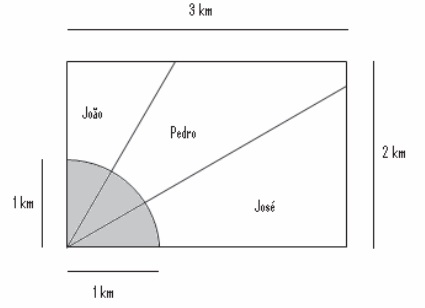
Em relação à partilha proposta, constata-se que a porcentagem da área do terreno que coube a João corresponde, aproximadamente, a
(considere \(\frac{\sqrt3}{3}\) = 0,58)
A) 50%
B) 43%
C) 33%
D) 33%
E) 19%
Questão 12
(Enem) As torres Puerta de Europa, construídas numa avenida de Madri, na Espanha, são inclinadas uma contra a outra. A inclinação das torres é de 15° com a vertical, e elas têm, cada uma, altura de 114 m (a altura é indicada na figura como o segmento AB). Essas torres são um bom exemplo de um prisma oblíquo de base quadrada, e uma delas pode ser observada na imagem.

Utilizando 0,26 como valor aproximado para a tangente de 15° e duas casas decimais nas operações, descobre-se que a área da base desse prédio ocupa na avenida um espaço
A) menor que 100 m².
B) entre 100 m² e 300 m².
C) entre 300 m² e 500 m².
D) entre 500 m² e 700 m².
E) maior que 700 m².
Resposta Questão 1
Alternativa A.
Sabemos que a tangente é a razão entre o cateto oposto e o cateto adjacente, então temos que:
\(\frac{x+2}{4x+1}=\frac{1}{2}\)
Multiplicando cruzado:
\(4x+1=2x+4\)
\(4x-2x=4-1\)
\(2x=3\)
\(x=\frac{3}{2}\)
Resposta Questão 2
Alternativa B.
Sabemos que a tangente é a razão entre o cateto oposto ao ângulo e o cateto adjacente, nessa ordem. Note que a medida do cateto oposto ao ângulo é de 5 unidades, e a medida do cateto adjacente ao ângulo é de 12 unidades, então essa razão é igual a \(\frac{5}{12}\).
Resposta Questão 3
Alternativa C.
A reta é tangente ao círculo quando ela toca a circunferência em um único ponto.
Resposta Questão 4
Alternativa C
I. A circunferência A é tangente interna à circunferência C. (verdadeiro)
Note na imagem que as circunferências de centro A e C são circunferências que se encontram em um único ponto.
II. O ponto de tangência dessas circunferências é o ponto B. (verdadeiro)
O ponto de encontro das circunferências é conhecido como ponto de tangente, e na imagem é possível perceber que esse ponto de fato está representado pelo ponto B.
Resposta Questão 5
Alternativa B.
Se a tangente do triângulo é igual a 1, sabemos que o ângulo notável que possui tangente igual a 1 é o ângulo de 45º. Sabemos que o triângulo é retângulo, logo ele possui um ângulo medindo 90º. Além disso, sabemos que um dos ângulos internos mede 45º.
Se a soma dos ângulos internos de um triângulo retângulo é 180º, sendo x a medida do outro ângulo, temos que:
\(180\ =\ 45\ +x\ +\ 90\)
\(180=135+x\)
\(180\ -\ 135\ =\ x\)
\(45° = x\)
Se temos dois ângulos internos medindo 45º e o outro ângulo medindo 90º, então o triângulo é isósceles.
Resposta Questão 6
Alternativa A.
Primeiro, faremos um esboço da situação.
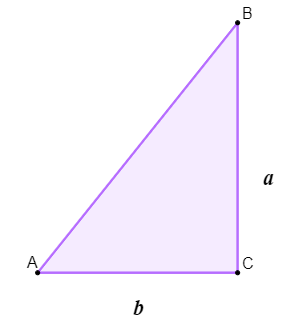
Seja C o ângulo reto, sabemos que a tangente do ângulo A é a razão entre a e b, que segundo o enunciado é igual a \(\sqrt3\), mas note que a é cateto oposto ao ângulo A, e b é cateto adjacente ao ângulo A. Sendo assim, podemos afirmar que \(tan\ A=\sqrt3\). Se a tangente de A é igual a \(\sqrt3\), o ângulo cuja tangente é \(\sqrt3\) é o ângulo de 60º.
Por fim sabemos que a soma dos ângulos internos de um triângulo é 180º. Se Â=60º e C = 90º, então B=30°.
Resposta Questão 7
Alternativa A.
Sabemos que a tangente é a razão entre o seno e o cosseno, logo:
\(\frac{\frac{2}{3}}{\frac{\sqrt5}{3}}\)
\(\frac{2}{3}\cdot\frac{3}{\sqrt5}\)
\(\frac{2}{\sqrt5}\)
Racionalizando, temos que:
\(\frac{2}{\sqrt5}\cdot\frac{\sqrt5}{\sqrt5}\)
\(\frac{2\sqrt5}{5}\)
Resposta Questão 8
Alternativa D.
Para calcular a área, primeiro calcularemos a medida da base do triângulo, representada por x:
\(tan\ 60°=\frac{14,5}{x}\)
Sabendo que a tangente de 60° é igual a \(\sqrt3\), temos que:
\(\sqrt3=\frac{14,5}{x}\)
\(1,7=\frac{14,5}{x}\)
\(1,7x\ =\ 14,5\)
\(x=\frac{14,5}{1,7}\)
\(x=8,5\ m\)
Calculando a área:
\(A=\frac{b\cdot h}{2}\)
\(A=\frac{8,5\cdot14,5}{2}\)
\(A=\frac{123,25}{2}\)
\(A=61,625\ m^2\)
Resposta Questão 9
Alternativa E.
Para calcular o perímetro do retângulo, calcularemos o valor de x, utilizando a tangente:
\(tan\ 30°=\frac{x}{8}\)
\(\frac{\sqrt3}{3}=\frac{x}{8}\)
\(0,58=\frac{x}{8}\)
\(0,58\ \cdot8\ =\ x\)
\(4,64\ =\ x\)
Agora, calcularemos o perímetro:
\(P=2\left(8+4,64\right)=2\cdot12,64=25,28\ cm\)
Resposta Questão 10
Alternativa D.
Sabemos que \(tan\ x=\frac{sen\ x}{cos\ x}\), então temos que:
\(0,3443=\frac{0,3256}{cosx}\)
\(0,3443\ cosx\ =\ 0,3256\)
\(cosx=\frac{0,3256}{0,3443}\)
\(cos\ x=0,9457\)
Resposta Questão 11
Alternativa E.
Sabemos que a área total do terreno mede \(3\cdot2=6\ km^2\). Se o ângulo é o mesmo, sabemos que o triângulo que representa a parte que coube ao João possui um ângulo de 30º, pois 90°: 3 = 30°.
No triângulo a seguir temos a área que coube ao João:
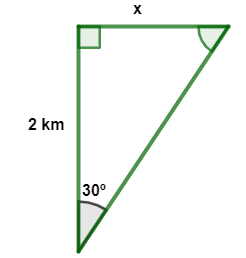
Para encontrar o valor de x, utilizaremos a área.
\(tan\ 30°=\frac{x}{2}\)
\(\frac{\sqrt3}{3}=\frac{x}{2}\)
\(0,58=\frac{x}{2}\)
\(2\ \cdot0,58\ =\ x\)
\(1,16=x\)
Se x = 1,16, então a área que coube ao João mede:
\(A=\frac{b\cdot h}{2}\)
\(A=\frac{1,16\cdot2}{2}\)
\(A=1,16\ km^2\)
Calculando a porcentagem a área total, temos:
\(1,16\ ∶\ 6\ =\ 0,1933\ldots\ \ =\ 19,3%\)
Aproximadamente 19%.
Resposta Questão 12
Alternativa E.
O segmento AB divide o prédio em dois triângulos retângulos, sabendo que o ângulo B é igual a 15º e que conhecemos o cateto adjacente a ele, é possível calcular o tamanho da base utilizando a tangente.
\(tan\ 15°=\frac{CO}{CA}\)
\(0,26=\frac{x}{114}\)
\(0,26\ \cdot114\ =\ x\)
\(29,64=x\)
Então, a área da base da torre mede 29,64² = 878,53 m², que é maior que 700.
Como a base é um quadrado, sua área será 29,64² = 878,53.



