Questão 1
Calculando a raiz quadrada de 2304, encontramos como solução:
A) 42
B) 44
C) 48
D) 52
E) 54
Questão 2
Uma região no formato de quadrado possui área igual a 729 m². Diante disso, qual é a medida do lado dessa região, em metros?
A) 19
B) 21
C) 23
D) 25
E) 27
Questão 3
Ao resolver a seguinte expressão:
\(\sqrt{\sqrt{81}}+\sqrt{16}-\sqrt{225}+\sqrt{144}\)
Encontramos como resultado
A) 1
B) 2
C) 3
D) 4
E) 5
Questão 4
Um retângulo possui comprimento e largura medindo, respectivamente, \(\sqrt{18}\) e \(\sqrt{72}\) metros. O perímetro desse retângulo, em metros, é de:
A) \(2\sqrt3\)
B) \(9\sqrt2\)
C) \(18\sqrt2\)
D) \(15\sqrt3\)
Questão 5
Sobre as propriedades da raiz quadrada, julgue as afirmativas a seguir:
I. \(\ \sqrt4\cdot\sqrt5=\sqrt{20}\)
II. \(\ \sqrt2+\sqrt3=\sqrt5\)
III. \(\sqrt4\ -\sqrt3=\sqrt1\)
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas I e II são verdadeiras.
E) Somente as afirmativas II e III são verdadeiras.
Questão 6
(Cefet/RJ 2015) Considere m a média aritmética dos números 1, 2, 3, 4 e 5. Qual é a opção que mais se aproxima do resultado da expressão abaixo?
![]()
A) 1,1
B) 1,2
C) 1,3
D) 1,4
Questão 7
(IFSC 2018) Analise as afirmações seguintes:
I. \(-5^2-\sqrt{16}\bullet\left(-10\right)\div\left(\sqrt5\right)^2=-17\)
II. \(35\div\left(3+\sqrt{81}-2^3+1\right)\times2=10\)
III. Efetuando-se \(\left(3+\sqrt5\right)\left(3-\sqrt5\right)\), obtém-se um número múltiplo de 2.
Assinale a alternativa CORRETA.
A) Todas são verdadeiras.
B) Apenas I e III são verdadeiras.
C) Todas são falsas.
D) Apenas uma das afirmações é verdadeira.
E) Apenas II e III são verdadeiras.
Questão 8
Sobre a raiz quadrada, julgue as afirmativas a seguir, utilizando V para verdadeira e F para falsa:
I. \(\sqrt{-4}=-2\)
II. \(\sqrt{2+7}=\sqrt2+\sqrt7\)
III. \(\sqrt{\sqrt{16}}\ =\ 2\)
As afirmativas são, respectivamente:
A) FFF
B) VVV
C) VFF
D) FFV
E) FVV
Questão 9
(PM Piauí 2009 Nucepe) A expressão \(\sqrt{18}+\sqrt{50}\) é equivalente a:
A) \(\ 2\sqrt2\)
B) \(\ 3\sqrt2\)
C) \(8\sqrt2\)
D) \(15\sqrt2\)
E) \(8\sqrt3\)
Questão 10
Simplificando a seguinte expressão:
\(\sqrt{4\ -\ \sqrt5}\ \cdot\sqrt{4+\sqrt5}\)
encontramos como resultado
A) 2
B) 3
C) 4
D) 6
E) 9
Questão 11
Sabendo que os lados do seguinte retângulo foram dados em metros, a forma simplificada da área desse polígono é igual a:
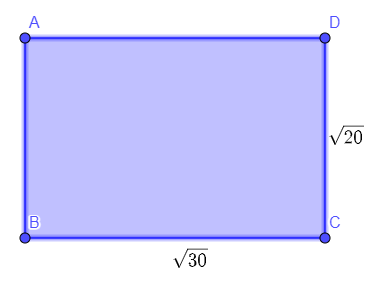
A) \(5\sqrt6\) m
B) \(10\sqrt6\) m
C) \(6\sqrt5\) m
D) \(5\sqrt2\) m
E) \(\ 4\sqrt{10}\) m
Questão 12
(UFPI) Desenvolvendo a expressão:
\(\left(\sqrt[2]{27}+\sqrt[2]{3}-1\right)^2\)
Encontramos um número no formato:
\(a+b\sqrt[2]{3}\)
Com a e b inteiros. O valor de a + b é:
A) 59
B) 47
C) 41
D) 57
E) 1
Resposta Questão 1
Alternativa C
Realizando a fatoração de 2304:
2304 = \(2^2\cdot2^2\cdot2^2\cdot2^2\cdot3^2\)
Portanto:
\(\sqrt{2304}=\sqrt{2^2\cdot2^2\cdot2^2\cdot2^2\cdot3^2}=2\cdot2\cdot2\cdot2\cdot3=48\)
Resposta Questão 2
Alternativa E
Para encontrar a medida do lado da região que possui formato de quadrado, basta calcularmos a raiz quadrada de 729.
Logo, temos que:
\(729=3^2\cdot3^2\cdot3^2\)
\(\sqrt{729}=\sqrt{3^2\cdot3^2\cdot3^2}=3\cdot3\cdot3=\ 27\ m\)
Resposta Questão 3
Alternativa B
Calculando cada uma das raízes quadradas:
\(\sqrt9+4-15+12\)
\(3\ +\ 4\ -\ 15\ +\ 12\)
\(4\ \)
Resposta Questão 4
Alternativa C
Sabemos que:
\(18=3^2\cdot2\)
\(72=2^2\cdot2\cdot3^2\)
Logo, temos que:
\(\sqrt{18}=\sqrt{3^2\cdot2}=3\sqrt2\)
\(\sqrt{72}=\sqrt{2^2\cdot2\cdot3}=2\cdot3\sqrt2=6\sqrt2\)
Portanto, o perímetro desse retângulo é igual a:
\(P=2\left(3\sqrt2+6\sqrt2\right)\)
\(P=2\cdot9\sqrt2\)
\(P=18\sqrt2\)
Resposta Questão 5
Alternativa A
I. Verdadeira
Uma das propriedades da raiz quadrada é que podemos multiplicar o radicando, como foi feito. Logo, temos que:
\(\sqrt4\cdot\sqrt5=\sqrt{4\cdot5}=\sqrt{20}\)
II. Falsa
A soma de duas raízes gera resultado diferente da soma dos radicandos. Assim, não podemos somá-los.
III. Falsa
A diferença de duas raízes não é igual à diferença dos seus radicandos, logo, essa não é uma propriedade da raiz quadrada.
Resposta Questão 6
Alternativa D
De início, calcularemos a média aritmética entre 1, 2, 3, 4 e 5:
\(m=\frac{1+2+3+4+5}{5}\)
\(m=\frac{15}{5}\)
\(m\ =\ 3\)
Substituindo m = 1 na expressão:
\(\sqrt{\frac{\left(1-3\right)^2+\left(2-3\right)^2+\left(3-3\right)^2+\left(4-3\right)^2+\left(5-3\right)^2}{5}}\)
\(\sqrt{\frac{\left(-2\right)^2+\left(-1\right)^2+0^2+1^2+2^2}{5}}\)
\(\sqrt{\frac{4+1+0+1+4}{5}}\)
\(\sqrt{\frac{10}{5}}\)
\(\sqrt2\ \approx1,4\)
Resposta Questão 7
Alternativa B
I. Verdadeira
\(-5^2-\sqrt{16}\bullet\left(-10\right)\div\left(\sqrt5\right)^2=-17\)
\(-25-4\bullet\left(-10\right)\div5=-17\)
\(-25\ +\ 40\ \div\ 5\ =\ -17\)
\(-25\ +\ 8\ =\ -17\)
\(-17\ =\ -17\)
II. Falsa
\(35\div\left(3+\sqrt{81}-2^3+1\right)\times2=10\)
\(35\div\left(3+9-8+1\right)\times2=10\)
\(35\ \div\ 5\ \times\ 2\ =10\)
\(7\ \times\ 2\ =10\)
\(14\ =10\ \)
III. Verdadeira
\(\left(3+\sqrt5\right)\left(3-\sqrt5\right)=3^2-\sqrt{5^2}\ =\ 9\ -\ 5\ =\ 4\)
Resposta Questão 8
Alternativa D
I. Falsa
Não há raiz quadrada de números negativos.
II. Falsa
Sabemos que 2 + 7 = 9 e que \(\sqrt9=3\). Por outro lado, \(\sqrt2+\sqrt7\ \) é diferente de 3, logo, essa não é uma propriedade possível para a radiciação.
III. Verdadeira
\(\sqrt{\sqrt{16}}=\sqrt4=2\)
Resposta Questão 9
Alternativa C
Simplificando, temos que:
\(\sqrt{18}+\sqrt{50}\)
\(\sqrt{2\cdot9}+\sqrt{2\cdot25}\)
\(3\sqrt2+5\sqrt2\)
\(8\sqrt2\)
Resposta Questão 10
Alternativa B
\(\sqrt{4\ -\ \sqrt5}\ \cdot\sqrt{4+\sqrt5}\)
\(\sqrt{\left(4-\sqrt5\right)\cdot\left(4+\sqrt5\right)}\)
\(\sqrt{4^2-\sqrt{5^2}}\)
\(\sqrt{16-5}\)
\(3\)
Resposta Questão 11
Alternativa B
Sabemos que a área do retângulo é igual ao produto da base pela altura:
\(A=\sqrt{30}\cdot\sqrt{20}\)
\(A=\sqrt{30\cdot20}\)
\(A\ =\ \sqrt{\left(3\cdot5\cdot2\right)\cdot\left(2^2\cdot5\right)}\)
\(A=\sqrt{3\cdot2\cdot2^2\cdot5^2}\)
\(A=2\cdot5\sqrt{3\cdot2}\)
\(A=10\sqrt{6\ }\)
Resposta Questão 12
Alternativa C
Simplificando a expressão:
\(\left(\sqrt[2]{27}+\sqrt[2]{3}-1\right)^2\)
\(\left(\sqrt[2]{3\cdot3^2}+\sqrt[2]{3}-1\right)^2\)
\(\left(3\sqrt[2]{3}+\sqrt[2]{3}-1\right)^2\)
\(\left(4\sqrt[2]{3}-1\right)^2\)
Calculando o quadrado da diferença:
\(16\cdot3-2\cdot4\sqrt[2]{3}+1^2\)
\(48-8\sqrt[2]{3}+1\)
\(49-8\sqrt[2]{3}\)
Se a = 49 e b = – 8, então:
a + b = 49 – 8 = 41



