Questão 1
Uma caixa possui formato de um cubo, com volume igual a 64 m³, então a medida do lado dessa caixa é igual a:
A) 21 m
B) 12 m
C) 8 m
D) 4 m
E) 2 m
Questão 3
Analise as afirmativas a seguir, e julgue-as como verdadeiras ou falsas.
I. \(\sqrt[3]{x}\), existe para todo x pertencente ao conjunto dos números reais, inclusive para os reais negativos.
II. \(\sqrt[3]{5}\cdot \sqrt[3]{4}=\sqrt[9]{20}\)
III. \(\sqrt[3]{24}:\sqrt[3]{8}=\sqrt[3]{3}\)
Marque a alternativa correta:
A) As afirmativas I, II e III são verdadeiras.
B) Somente as afirmativas I e II são verdadeiras
C) Somente as afirmativas II e III são verdadeiras.
D) Somente as afirmativas I e III são verdadeiras.
Questão 4
A raiz cúbica entre o produto entre um número n e a fração \(\frac{2}3\) é igual a 3. Então podemos afirmar que n é igual a:
A) 35,5
B) 38,0
C) 40,5
D) 42,0
E) 45,5
Questão 5
Calculando \((∛(-125)+∛8)^2\), encontramos como resposta:
A) 9
B) 5
C) 3
D) -3
E) -2
Questão 6
Qual é o valor simplificado da expressão numérica:
\(\sqrt[3]{27}+2\sqrt[3]{216}-\sqrt[3]{512}\)
A) 15
B) 8
C) 7
D) 5
E) 1
Questão 7
Uma região é delimitada por um triângulo, com lados medindo \(\sqrt[3]{40}\) m, \(\sqrt[3]{320}\) m e \(\sqrt[3]{625}\) m. O perímetro dessa região, em metros, é igual a:
A) 1135
B) 635
C) 535
D) 11
E) 17
Questão 8
O cilindro C possui o seu raio igual a sua altura e volume igual a 5184 cm³. Sabendo que o volume do cilindro é calculando pela fórmula \(V=πr^2⋅h\), em que r é o seu raio e h é a sua altura, e utilizando π = 3, então o valor do raio desse cilindro é:
A) 10 cm
B) 12 cm
C) 14 cm
D) 16 cm
E) 24 cm
Questão 9
Durante algumas medições, o engenheiro constatou que a medida de determinada viga metálica em metros era igual à raiz cúbica de 253, logo, podemos afirmar que a medida dessa viga está entre:
A) 9 e 10 metros
B) 8 e 9 metros
C) 7 e 8 metros
D) 6 e 7 metros
E) 5 e 6 metros
Questão 10
Qual é o valor que mais se aproxima de \(\sqrt[3]{80}\)?
A) 4,1
B) 4,2
C) 4,3
D) 4,4
E) 4,5
Questão 11
A raiz cúbica do número 10 ao quadrado está entre:
A) 4 e 5
B) 5 e 6
C) 6 e 7
D) 7 e 8
E) 8 e 9
Questão 12
Qual é o valor da expressão:
\(\sqrt[3]{\frac{5^{27}+5^{29}}{26}}\)
A) 55
B) 56
C) 57
D) 58
E) 59
Resposta Questão 1
Alternativa D
Se a caixa possui formato de um cubo, então sabemos que o seu volume é igual à medida do lado ao cubo, logo, sabemos que:
\(l^3=64\)
\(l=\sqrt[3]{64}\)
\(l=4\ \)
Resposta Questão 2
Alternativa A
Para calcular a raiz cúbica de 216, é necessário fatorar esse número:
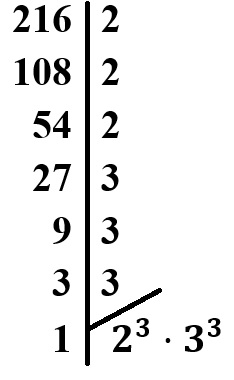
Então temos que:
\(\sqrt[3]{216}=\sqrt[3]{2^3\cdot3^3}\)
\(\sqrt[3]{216}=2\cdot3\)
\(\sqrt[3]{216}=6\)
Resposta Questão 3
Alternativa D
I. \(\sqrt[3]{x}\) existe para todo x pertencente ao conjunto dos números reais, inclusive para os reais negativos. (verdadeira)
II. \(\sqrt[3]{5}\cdot \sqrt[3]{4}=\sqrt[9]{20}\) (falso)
Não há alteração no índice da raiz, o correto seria:
\(\sqrt[3]{5}\cdot \sqrt[3]{4}=\sqrt[3]{20}\)
III. \(\sqrt[3]{24}:\sqrt[3]{8}=\sqrt[3]{3}\) (verdadeiro)
Na divisão de duas raízes cúbicas, podemos dividir os radicandos e conservar a raiz cúbica.
Resposta Questão 4
Alternativa C
Sabemos que:
\(\sqrt[3]{n\cdot \frac{2}{3}}=3\)
Então temos que:
\(\Big(\sqrt[3]{n\cdot \frac{2}{3}}\Big)^3=3^3\)
\(n⋅\frac{2}3=27\)
\(n ⋅2 = 27 ⋅3\)
\(n⋅2 = 81\)
\(n=\frac{81}2\)
Resposta Questão 6
Alternativa C
Primeiro resolveremos as raízes. Sabemos que:
\(\sqrt[3]{27}=3\)
\(\sqrt[3]{216}=6\)
\(\sqrt[3]{512}=8\)
Logo, temos que:
\(\sqrt[3]{27}+2\sqrt[3]{216}-\sqrt[3]{512}=3+2⋅6-8=3+12-8=15-8=7\)
Resposta Questão 7
Alternativa A
Calculando o perímetro, temos que:
\(P=\sqrt[3]{40}+\sqrt[3]{320}+\sqrt[3]{625}\)
Por outro lado, sabemos que:
\(\sqrt[3]{40}=\sqrt[3]{2^3\cdot 5}=2\sqrt[3]{5}\)
\(\sqrt[3]{320}=\sqrt[3]{2^6\cdot 5}=2^{2\sqrt[3]{5}}=4\sqrt[3]{5}\)
\(\sqrt[3]{625}=\sqrt[3]{5^4}=5\sqrt[3]{5}\)
Então, somando esses valores, encontraremos o perímetro:
\(P=2\sqrt[3]{5}+4\sqrt[3]{5}+4\sqrt{35}=11\sqrt[3]{5}\)
Resposta Questão 8
Alternativa B
Sabemos que o volume de um cilindro é calculado pela seguinte fórmula:
\(V=πr^2⋅h\)
Como π=3 , V = 5184 e h = r, temos que:
\(5184=3⋅r^2⋅r\)
\(5184=3r^3\)
\(\frac{5184}3=r^3\)
\(1728=r^3\)
\(r=\sqrt[3]{1728}\)
\(r=12\)
O raio é de 12 cm.
Resposta Questão 9
Alternativa D
A raiz cúbica de 253 está entre 6 e 7, pois sabemos que:
\(6^3=216\)
\(7^3=343\)
Logo, a medida da viga está entre 6 e 7 metros.
Resposta Questão 10
Alternativa C
Sabemos que \(\sqrt[3]{80}\) não é uma raiz cúbica exata, mas está entre a raiz cúbica de 4 e de 5, pois temos que:
\(4^3=64\)
\(5^3=125\)
Logo, temos que:
\(4<\sqrt[3]{80}<5\)
Testando as possibilidades:
4,1³ = 68,92
4,2³ = 74,09
4,3³ = 79,51
4,4³ = 85,18
Então o valor que mais se aproxima da raiz cúbica de 80 é 4,3.
Resposta Questão 11
Alternativa A
Sabemos que 10² = 100.
A raiz cúbica de 100 não é exata, então encontraremos entre quais raízes cúbicas exatas 100 se encontra.
Sabemos que:
4³ = 64
5³ = 125
Como 100 está entre 64 e 125, então a raiz cúbica de 100 está entre 4 e 5.
Resposta Questão 12
Alternativa E
\(\sqrt[3]{\frac{5^{27}⋅(1+5^2)}{26}}\)
\(\sqrt[3]{\frac{5^{27}⋅(1+25)}{26}}\)
\(\sqrt[3]{\frac{5^{27}⋅26}{26}}\)
\(\sqrt[3]{5^{27}}\)
\(5^\frac{27}{3}\)
\(5^9\)



