Questão 1
O conjunto de valores que satisfaz a inequação a seguir é:
![]()
A) x ≤ 0
B) x ≤ 1
C) x ≤ 2
D) x ≤ 3
E) x ≤ 4
Questão 2
Dada a função exponencial y = 3(x – 4), há um conjunto de valores que faz com que 1 < y < 27. A soma das soluções naturais é igual a:
A) 15
B) 11
C) 10
D) 6
E) 5
Questão 3
(EsPCEx) A quantidade de números inteiros ímpares que pertencem ao intervalo que satisfaz a inequação exponencial a seguir é de:
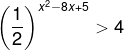
A) um número ímpar.
B) dois números ímpares.
C) três números ímpares.
D) quatro números ímpares
E) cinco números ímpares.
Questão 4
A quantidade de bactérias de uma cultura evolui de acordo com a função Q(t) = K · 1,5t., sendo t o tempo em horas. Para fazer um experimento, havia inicialmente um total de 1200 bactérias, mas eram necessárias, no mínimo, 6075 bactérias. O tempo mínimo de espera para conseguir a quantidade desejada na amostra é de:
A) pelo menos 2 horas.
B) pelo menos 3 horas.
C) pelo menos 4 horas.
D) pelo menos 5 horas e 30 minutos.
E) pelo menos 6 horas.
Questão 5
Marque a alternativa que representa o conjunto de soluções da inequação a seguir:
7x – 2 ≤ 49
A) ] – ∞, 4]
B) [ 2, +∞[
C) ] – ∞, 2]
D) [4, +∞[
Questão 6
Uma loja de veículos acredita que o valor de um determinado veículo V(t), no decorrer do tempo em anos, é dado pela lei de formação V(t) = 60.000 · 0,9t. Mariana comprou esse veículo e deseja vendê-lo até ele atingir no mínimo o valor de R$ 39.366,00. Então, o tempo de uso desse veículo tem que ser de:
A) no máximo 6 anos de uso.
B) no máximo 5 anos de uso.
C) no máximo 4 anos de uso.
D) no máximo 3 anos de uso.
E) no máximo 2 anos de uso.
Questão 7
(EsPCEx – Cadete 2011) A inequação 10x + 10x+1 + 10x+2 + 10x+3 + 10x+4 <11111, em que x é um número real:
A) não tem solução.
B) tem apenas uma solução.
C) tem apenas soluções positivas.
D) tem apenas soluções negativas.
E) tem soluções positivas e negativas
Questão 8
(UEL-PR) A relação a seguir descreve o crescimento de uma população de micro-organismos, sendo P o número de micro-organismos, t dias após o instante 0. O valor de P é superior a 63 000 se, e somente se, t satisfizer à condição: P = 64 000·(1 – 2-0,1t)
A) 2 < t < 16
B) t > 16
C) t < 30
D) t > 60
E) 32 < t < 64
Questão 9
(AFA) O conjunto de solução da inequação (0,5)x(x– 2)< (0,25)x –1,5 é:
a) {x ∈ IR | x <1}.
b) {x ∈ IR | x >3}.
c) {x ∈ IR | 1 < x <3}.
d) {x ∈ IR | x < 1 ou x > 3}.
Questão 10
Das alternativas a seguir, marque aquela que representa uma inequação exponencial.
A) 2x+1 + 4 – 16x- 8
B) 2x + 5 < 3
C) 5x+1 = 25
D) logx + 3 ≥ x
E) 2x + x > x – 1
Questão 11
A soma das soluções naturais da inequação 3x – 3 ≤ 81 é igual a:
A) 21
B) 28
C) 32
D) 35
E) 40
Questão 12
Durante a resolução de problemas envolvendo funções exponenciais, Márcia se deparou com uma inequação exponencial:
1 ≤ 2x+1 ≤ 32
Sabendo que x é um número real, o conjunto de soluções dessa inequação é:
A) – 1 ≤ x ≤ 3
B) 1 ≤ x ≤ 4
C)– 2 ≤ x ≤ 5
D) 1 ≤ x ≤ 32
E)– 1 ≤ x ≤ 4
Resposta Questão 1
Alternativa C.
Para encontrar o conjunto de soluções, vamos igualar as bases dos dois lados.
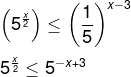
Agora que igualamos as bases, vamos representar a desigualdade dos expoentes. Como a base é maior que 1, basta preservar a desigualdade:
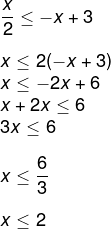
Resposta Questão 2
Alternativa B.
Queremos que:
1 < 3(x – 4) < 27
Igualando as bases, temos que:
30 < 3(x – 4) < 33
Como igualamos as bases e elas são maiores que 1, então:
0 < x – 4 < 3
Somando 4 em todos os lados da desigualdade, temos que:
0 + 4 < x – 4 + 4 < 3 + 4
4 < x < 7
Os números naturais que estão entre 4 e 7 são o 5 e o 6. A soma de 5 + 6 = 11.
Resposta Questão 3
Alternativa B.
Vamos igualar as bases para igualar os expoentes:
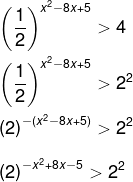
Agora que igualamos as bases, vamos representar a desigualdade dos exponentes:
– x² + 8x – 5 > 2
– x² + 8x – 5 – 2 > 0
– x² + 8x – 7 > 0
Encontramos uma equação do 2º grau. Calculando delta e Bhaskara, temos que:
-
a = – 1
-
b = 8
-
c = – 7
Δ = b² – 4ac
Δ = 8² – 4 ( – 1) ( – 7)
Δ = 64 – 28
Δ = 36
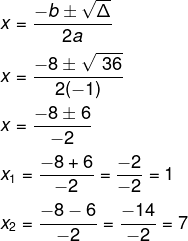
Na equação do 2º grau, temos a = – 1, logo o conjunto de soluções inteiras são os números que estão entre 1 e 7, ou seja, 2, 3, 4, 5 e 6, havendo dois números ímpares.
Resposta Questão 4
Alternativa C.
Queremos encontrar o valor de t tal que 6075 ≤ Q(t). Além disso, sabemos que K = 1200.
6075 ≤ 1200 · 1,5t.
6075 : 1200 ≤ 1,5t
5,0625 ≤ 1,5t
1,54 ≤ 1,5t
Agora que igualamos as bases, podemos escrever a desigualdade dos expoentes:
4 ≤ t
Logo, são necessárias pelo menos 4 horas.
Resposta Questão 5
Alternativa A.
Vamos igualar as bases:
7x – 2 ≤ 49
7x – 2 ≤ 7²
Agora escreveremos a desigualdade dos expoentes:
x – 2 ≤ 2
x ≤ 2 + 2
x ≤ 4
Logo, o conjunto de soluções é o conjunto ] – ∞, 4].
Resposta Questão 6
Alternativa C.
Queremos que V(t) ≥ 39366:
60.000 · 0,9t ≥ 39366
0,9t ≥ 39366 : 60000
0,9t ≥ 0,6561
0,9t ≥ 0,94
Como a base é menor que 1, vamos inverter a desigualdade:
t ≤ 4
Logo, ela poderá usar esse veículo por no máximo 4 anos.
Resposta Questão 7
Alternativa D.
Temos que:
10x + 10x+1 + 10x+2 + 10x+3 + 10x+4 <11111
Colocando 10x em evidência:
10x + 10x·10¹ + 10x·102 + 10x ·103 + 10x·104 <11111
10x · (1 + 101 + 102 + 103 + 104) < 11111
10x · (1 + 10 + 100 + 1000 + 10000) < 11111
10x · 11111 < 11111
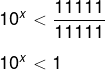
Sabemos que 100 = 1.
10x < 100
x < 0
Como x é menor que 0, então as soluções são sempre negativas.
Resposta Questão 8
Alternativa D.
Temos que:
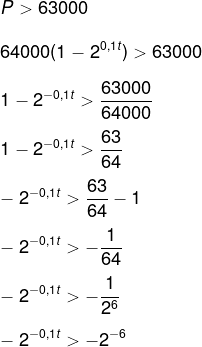
Agora que igualamos as bases e como elas são menores que 1, vamos inverter a desigualdade dos expoentes:
– 0,1t < – 6
– t < – 6 : 0,1
– t < – 60 ( – 1)
t > 60
Resposta Questão 9
Alternativa D.
Vamos igualar as bases:
(0,5)x(x– 2)< (0,25)x –1,5
(0,5)x(x– 2)< (0,5²)x –1,5
(0,5)x(x– 2)< (0,5)²x –3
Como a base é menor que 1, para escrever a desigualdade entre os expoentes, vamos inverter a desigualdade:
x(x – 2) > 2x – 3
x² – 2x > 2x – 3
x² – 2x – 2x + 3 > 0
x² – 4x + 3 > 0
Encontramos uma equação do 2º grau, em que a = 1, b = – 4 e c = 3.
Δ = b² – 4ac
Δ = ( – 4)² – 4 · 1 · 3
Δ = 16 – 12
Δ = 4
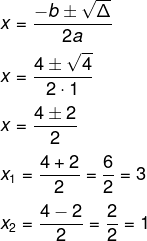
Sabemos que a = 1. Como ele é positivo, as soluções são os números menores que 1 ou maiores que 3:
{x ∈ IR | x < 1 ou x > 3}
Resposta Questão 10
Alternativa E.
Das alternativas apresentadas, somente a alternativa E descreve uma inequação exponencial.
Resposta Questão 11
Alternativa B.
Vamos igualar as bases:
3x – 3 ≤ 81
3x – 3 ≤ 34
3x – 3 ≤ 34
Agora que igualamos as bases, podemos escrever a inequação dos expoentes:
x – 3 ≤ 4
x ≤ 4 + 3
x ≤ 7
Então, as soluções naturais são os números menores ou iguais a 7. São eles: 1, 2, 3, 4, 5, 6 e 7. Realizando a soma, temos que:
1+2+3+4+5+6+7 = 28
Resposta Questão 12
Alternativa A.
Igualando as bases, temos que:
1 ≤ 2x+1 ≤ 32
20≤ 2x+1 ≤ 24
Agora que igualamos as bases, podemos escrever a desigualdade dos expoentes:
0 ≤ x+1 ≤ 4
Subtraindo 1 em todos os membros, temos que:
0 – 1 ≤ x + 1 – 1 ≤ 4 – 1
– 1 ≤ x ≤ 3



