Questão 1
São considerados sólidos geométricos, exceto:
A) cone
B) cilindro
C) esfera
D) cubo
E) triângulo
Questão 2
Após se aposentar, Kárita decidiu se dedicar mais ao seu hobbie de fazer desenhos e pinturas. Pensando no ambiente em que ela faria os desenhos, ela decidiu reformar um quarto da sua casa, começando pela pintura da parede do teto e das paredes laterais desse cômodo. Sabendo que esse quarto possui formato de um paralelepípedo retângulo com 4 metros de comprimento, 5 metros de largura e 2,5 metros de altura, a medida da área a ser pintada é de:
A) 48 m²
B) 52 m²
C) 60 m²
D) 65 m²
E) 72 m²
Questão 3
As embalagens de joias de uma empresa possuem o seguinte formato quando planificadas:
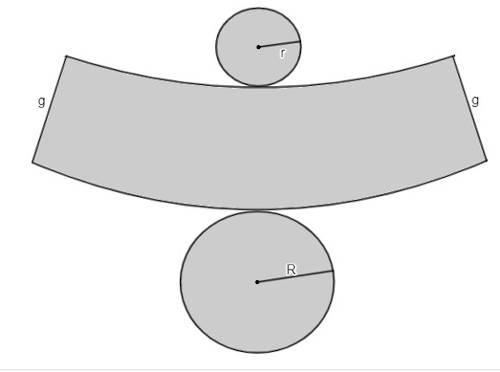
Analisando a planificação, podemos afirmar que essas embalagens possuem formato de:
A) cilindro
B) prisma de base circular
C) cone
D) tronco de cone
E) pirâmide
Questão 4
Um recipiente possui o formato do sólido geométrico a seguir:
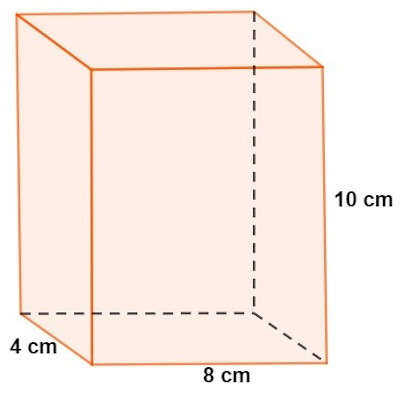
Se que a metade dele está ocupada, então o volume restante desse recipiente é de:
A) 22 cm³
B) 32 cm³
C) 40 cm³
D) 160 cm³
E) 320 cm³
Questão 5
Após as aulas de Geometria Espacial, na volta de ônibus para casa, Julia observou melhor o espaço à sua volta, na busca de objetos que possuíssem formato de um sólido geométrico. Após a observação, Júlia fez as seguintes anotações:
I – A bola de futebol possui formato de uma esfera, que é um corpo redondo.
II – O cilindro é um prisma de base circular.
III – Todo corpo redondo é um poliedro.
Analisando as afirmativas feitas por Júlia, marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Nenhuma das afirmativas é verdadeira.
Questão 6
Sobre a posição relativa entre as retas de um mesmo plano, há 3 possibilidades: retas paralelas, retas concorrentes e retas coincidentes. Analisando essas classificações possíveis, temos que:
A – retas paralelas
B – retas coincidentes
C – retas concorrentes
( ) são retas que possuem um único ponto em comum.
( ) são retas que possuem infinitos pontos em comum.
( ) são retas que não possuem pontos em comum.
A alternativa que contém a ordem correta das definições é:
A) A – B – C
B) B – C – A
C) C – A – B
D) C – B – A
E) B – A – C
Questão 7
Em uma floricultura, os vasos de flores possuem o formato do sólido geométrico representado na imagem a seguir:
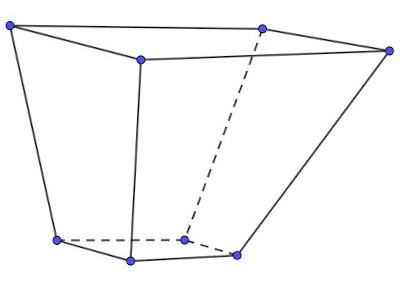
Analisando a forma geométrica, podemos afirmar que esse sólido é um(a)
A) prisma
B) tronco de prisma
C) pirâmide
D) tronco de pirâmide
E) cone
Questão 8
Um poliedro regular possui 32 faces e 20 vértices. Então, o número de arestas desse poliedro é:
A) 35
B) 40
C) 45
D) 50
E) 55
Questão 9
(Enem – 2019 – PPL) No ano de 1751, o matemático Euler conseguiu demonstrar a famosa relação para poliedros convexos que relaciona o número de suas faces (F), arestas (A) e vértices (V): V + F = A + 2. No entanto, na busca dessa demonstração, essa relação foi sendo testada em poliedros convexos e não convexos. Observou-se que alguns poliedros não convexos satisfaziam a relação e outros não. Um exemplo de poliedro não convexo é dado na figura. Todas as faces que não podem ser vistas diretamente são retangulares.
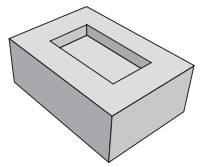
Qual a relação entre os vértices, as faces e as arestas do poliedro apresentado na figura?
A) V + F = A
B) V + F = A - 1
C) V + F = A + 1
D) V + F = A + 2
E) V + F = A + 3
Questão 10
(Enem 2017) Um casal realiza sua mudança de domicílio e necessita colocar numa caixa de papelão um objeto cúbico, de 80 cm de aresta, que não pode ser desmontado. Eles têm à disposição cinco caixas, com diferentes dimensões, conforme descrito:
• Caixa 1: 86 cm x 86 cm x 86 cm
• Caixa 2: 75 cm x 82 cm x 90 cm
• Caixa 3: 85 cm x 82 cm x 90 cm
• Caixa 4: 82 cm x 95 cm x 82 cm
• Caixa 5: 80 cm x 95 cm x 85 cm
O casal precisa escolher uma caixa na qual o objeto caiba, de modo que sobre o menor espaço livre em seu interior. A caixa escolhida pelo casal deve ser a de número
A) 1
B) 2
C) 3
D) 4
E) 5
Questão 11
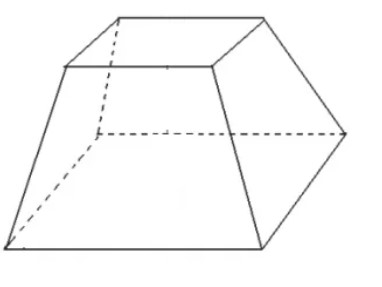
(Enem – 2020) Uma das Sete Maravilhas do Mundo Moderno é o Templo de Kukulkán, localizado na cidade de Chichén Itzá, no México. Geometricamente, esse templo pode ser representado por um tronco reto de pirâmide de base quadrada.
As quantidades de cada tipo de figura plana que formam esse tronco de pirâmide são
A) 2 quadrados e 4 retângulos.
B) 1 retângulo e 4 triângulos isósceles.
C) 2 quadrados e 4 trapézios isósceles.
D) 1 quadrado, 3 retângulos e 2 trapézios retângulos.
E) 2 retângulos, 2 quadrados e 2 trapézios retângulos.
Questão 12
(Enem 2012) Maria quer inovar sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas, estão as planificações dessas caixas.
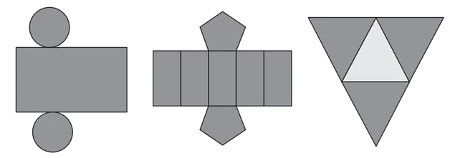
Quais serão os sólidos geométricos que Maria obterá por meio dessas planificações?
A) Cilindro, prisma de base pentagonal e pirâmide.
B) Cone, prisma de base pentagonal e pirâmide.
C) Cone, tronco de pirâmide e prisma.
D) Cilindro, tronco de pirâmide e prisma.
E) Cilindro, prisma e tronco de cone.
Resposta Questão 1
Alternativa E
O triângulo é uma figura plana, e não um sólido geométrico, pois ele possui 2 dimensões, e os sólidos geométricos possuem 3 dimensões.
Resposta Questão 2
Alternativa D
Sabemos que serão pintadas 5 áreas retangulares, sendo o teto e as 4 paredes laterais. As áreas laterais paralelas são congruentes, então para calcular a área pintada, temos que:
\(A_p=5⋅4+2⋅5⋅2,5+2⋅4⋅2,5\)
\(A_p=20+25+20=65\ m^2\)
Resposta Questão 3
Alternativa D
O sólido é um tronco de cone. Note que ele possui duas faces circulares de raios diferentes, característica do tronco de cone.
Resposta Questão 4
Alternativa D
Calculando o volume, temos que:
\(V=4⋅8⋅10 \)
\(V=32⋅10 \)
\(V=320\ cm^3\)
Como queremos o volume da metade do recipiente, dividiremos o volume por 2.
\(320∶2=160\ cm^3\)
Resposta Questão 5
Alternativa A
I – A bola de futebol possui formato de uma esfera, que é um corpo redondo. (Verdadeira)
A esfera de fato é um corpo redondo.
II – O cilindro é um prisma de base circular. (Falsa)
O cilindro não é um prisma, pois os prismas possuem base formada por um polígono, e o círculo não é um polígono.
III – Todo corpo redondo é um poliedro. (Falsa)
Um sólido geométrico pode ser um corpo redondo ou um poliedro. Enquanto os poliedros são sólidos geométricos formados apenas por polígonos cujas arestas são segmentos de reta, os corpos redondos são aqueles sólidos que possuem curvas em vez de alguma face e que, se colocados sobre uma superfície plana levemente inclinada, rolam.
Resposta Questão 6
Alternativa D
-
Retas concorrentes (C) são retas que possuem um único ponto em comum.
-
Retas coincidentes (B) são retas que possuem infinitos pontos em comum.
-
Retas paralelas (A) são retas que não possuem pontos em comum.
Resposta Questão 7
Alternativa D
Esse sólido geométrico é conhecido como tronco de pirâmide.
Resposta Questão 8
Alternativa E
Aplicando a relação de Euler, temos que:
F = 32
V = 20
A = ?
\(V+F=A+2\)
\(20+32=A+2\)
\(52=A+2\)
\(52-2=A\)
\(A=50\)
Resposta Questão 9
Alternativa E
Analisando a forma geométrica, podemos perceber que ela possui 16 vértices, 11 faces e 24 arestas.
Quando somamos vértice com face, temos que:
V + F = 16 + 11 = 27
Sabemos que 27 – 24 = 3
Então o número de V + F é igual a A + 3, logo a fórmula será:
V + F = A + 3
Resposta Questão 10
Alternativa C
Calculando o volume do objeto, que é um cubo:
\(V=80^3=512000\)
A caixa 2 e a caixa 5 possuem dimensões menores que 80 cm, logo o objeto não caberia nelas. Calculando o volume das demais caixas:
\(V_1=86⋅86⋅86=636056\)
\(V_3=85⋅82⋅90=627300\)
\(V_4=82⋅95⋅82=638780\)
A caixa com menor volume que comporta esse objeto é a caixa 3.
Resposta Questão 11
Alternativa C
Fazendo a representação do tronco da pirâmide, podemos perceber que ele possui 2 faces quadradas, que são as suas bases, e 4 faces laterais formadas por trapézios isósceles.
Resposta Questão 12
Alternativa A
Analisando as planificações, percebemos que a primeira delas corresponde a um cilindro; a segunda, a um prisma de base pentagonal; e a terceira, a uma pirâmide.



