Questão 1
Uma função é classificada como sobrejetora se:
A) todo elemento do domínio possui exatamente um correspondente no contradomínio.
B) todo elemento do contradomínio for correspondente de, pelo menos, um elemento no domínio.
C) todo elemento do contradomínio for correspondente de, pelo menos, dois elementos no domínio.
D) todo elemento do domínio possuir, pelo menos, um correspondente no contradomínio.
E) todo elemento do contradomínio for correspondente de um único elemento no domínio.
Questão 2
Dada a função \(f:\ \mathbb{R}\ \rightarrow\mathbb{R}\), cuja lei de formação é \(f\left(x\right)=2x^2\), então podemos afirmar que:
A) essa função não é sobrejetora porque \(f\left(n\right)=f\left(-n\right)\).
B) essa função é sobrejetora porque \( f\left(n\right)=f\left(-n\right)\).
C) essa função não é sobrejetora porque a imagem da função é \(\mathbb{R}_+\).
D) essa função é sobrejetora porque a imagem da função é \(\mathbb{R}_+\).
Questão 3
Analise a relação entre os conjuntos a seguir:
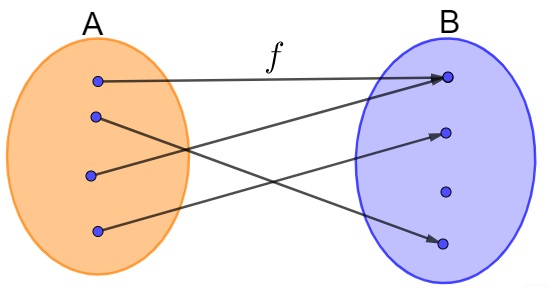
Podemos afirmar que:
A) essa relação não é uma função.
B) essa relação é uma função sobrejetora.
C) essa relação é uma função injetora.
D) essa relação é uma função, mas não é sobrejetora.
E) essa relação é uma função bijetora.
Questão 4
O diagrama a seguir representa uma relação entre dois conjuntos:
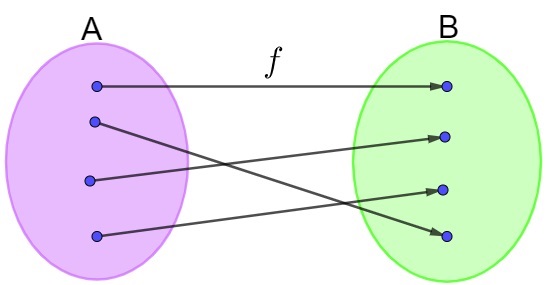
Analisando essa relação, podemos afirmar que:
I – É uma função sobrejetora.
II – É uma função injetora.
III – É uma função bijetora.
Marque a alternativa correta:
A) Somente a I é falsa.
B) Somente a II é falsa.
C) Somente a III é falsa.
D) Todas são verdadeiras.
Questão 5
A função \(f\left(x\right)=ax^2\), com \(a>0\) e domínio no conjunto dos números reais, pode ser sobrejetora quando o seu contradomínio for:
A) \(\mathbb{R}_+\)
B) \(\mathbb{R}_-\)
C) \(\mathbb{R}^\ast\)
D) \(\mathbb{R}_+^\ast\)
E) \(\mathbb{R}\)
Questão 6
(BIO- RIO) Na figura a seguir está evidenciada, através de setas, uma relação entre os elementos do conjunto A e os elementos do conjunto B.
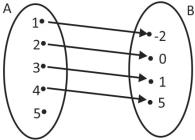
A respeito dessa relação, é correto afirmar que:
A) não é uma função.
B) é uma função que não é injetora nem sobrejetora.
C) é uma função injetora, mas não sobrejetora.
D) é uma função sobrejetora, mas não injetora.
E) é uma função bijetora.
Questão 7
A função com lei de formação \(f\left(x\right)=2x\) é sobrejetora se:
A) o domínio e o contradomínio forem o conjunto dos números naturais.
B) o domínio e o contradomínio forem o conjunto dos números inteiros.
C) o domínio e o contradomínio forem o conjunto dos números irracionais.
D) o domínio e o contradomínio forem o conjunto dos números racionais.
Questão 8
(IMA) Sobre funções injetoras, sobrejetoras e bijetoras, julgue os itens abaixo em verdadeiro ou falso.
I. Toda função injetora é bijetora.
II. Quando elementos diferentes geram imagens diferentes, temos uma função sobrejetora.
III. Toda função bijetora admite inversa.
VI. Quando a imagem é igual ao contradomínio, temos uma função sobrejetora.
A) V V V V
B) F F V V
C) V V F F
D) F F F F
Questão 9
(Fauel) Classifique a função f: A ⟶ B, f(x) = 3x². Sendo: domínio: D(f) = {-2, -1, 1, 3}, contradomínio: CD(f) = {12, 3, 27}, conjunto imagem: Im(f) = {12, 3, 27}.
A) Injetora
B) Sobrejetora
C) Bijetora
D) Nenhuma das anteriores
Questão 10
(IDCAP) Podemos classificar uma função sobrejetora como sendo aquela que possui o:
A) domínio constituído apenas de números naturais.
B) contradomínio com valores dobrados em relação ao conjunto imagem.
C) conjunto imagem nulo.
D) domínio diferente do conjunto contradomínio.
E) contradomínio igual ao conjunto imagem.
Questão 11
Analise as funções a seguir:
I. \(f:\ \mathbb{R}\rightarrow\mathbb{R}\ |\ f(x)=ax+b\)
II. \(f:\ \mathbb{R}\rightarrow\mathbb{R}\ |f\left(x\right)=-2x^2\ \)
III. \(f:\mathbb{R}\rightarrow\mathbb{R}|f\left(x\right)=2^x\ \)
Podemos classificar a função como sobrejetora:
A) somente na I
B) somente na II
C) somente na III
D) somente na I e III
E) em todas as funções
Questão 12
A função \(f:\ \mathbb{R}\ \rightarrow B\ \) possui lei de formação \(f\left(x\right)={-ax}^2\). Sabendo que \(a>0\), essa função é sobrejetora se:
A) B = \(\mathbb{R}\)
B) B = \(\mathbb{R}^\ast\)
C) B = \(\mathbb{R}_-\)
D) B = \(\mathbb{R}_+^\ast\)
E) B = \(\mathbb{R}_+\)
Resposta Questão 1
Alternativa B
A função é sobrejetora quando cada elemento do contradomínio da função for correspondente de, pelo menos, um elemento do domínio da função, ou seja, quando a imagem da função for igual ao contradomínio da função.
Resposta Questão 2
Alternativa C
Essa função não é sobrejetora, pois os números reais negativos não são imagem de nenhum elemento da função, logo, o conjunto imagem da função são os números reais positivos e o contradomínio é o conjunto dos números reais. Para que a função seja sobrejetora, é necessário que a imagem seja igual ao contradomínio da função, o que não acontece aqui, logo, essa função não é sobrejetora porque a imagem da função é \(\mathbb{R}_+\).
Resposta Questão 3
Alternativa D
Como podemos ver, todos os elementos do conjunto A possuem um correspondente no conjunto B, logo, essa relação é uma função, entretanto, há um elemento no conjunto B que não é correspondente de nenhum elemento do conjunto A, portanto, essa função não é sobrejetora. Assim, essa relação é uma função, mas que não é sobrejetora.
Resposta Questão 4
Alternativa D
I – Essa relação é uma função sobrejetora. (verdadeira)
Note que a imagem é igual ao contradomínio da função, pois não há nenhum elemento no conjunto B que não possua correspondente no conjunto A, então, é uma função sobrejetora.
II – Essa relação é uma função injetora. (verdadeira)
Note que dois elementos distintos do conjunto A possuem sempre imagens distintas no conjunto B, então, é uma função injetora.
III – Essa relação é uma função bijetora. (verdadeira)
Como a função é injetora e sobrejetora, então ela é bijetora.
Resposta Questão 5
Alternativa A
Como \(a\ \) é um número real sempre positivo, então \(f\left(x\right)\geq0\) para todo valor de x, pois sabemos que \(x^2\) é um número positivo, ou zero, e que a multiplicação entre dois números positivos gera como resultado um número positivo, bem como a multiplicação de um número por zero terá como resultado o zero. Sendo assim, o conjunto imagem da função é o conjunto \(\mathbb{R}_+\), e, para que a função seja sobrejetora, necessariamente o contradomínio tem que ser igual à imagem, ou seja, a função é sobrejetora se e somente se o contradomínio for o conjunto \(\mathbb{R}_+\).
Resposta Questão 6
Alternativa A
Analisando a relação, é possível perceber que ela não é uma função, pois existe elemento no conjunto A que não possui correspondente algum no conjunto B.
Resposta Questão 7
Alternativa D
A função é sobrejetora no conjunto dos números racionais, pois, dado um número racional \(n\) pertencente à imagem da função, existe um número \(\frac{n}{2}\) no domínio, tal que:
\(f\left(\frac{n}{2}\right)=n\)
Resposta Questão 8
Alternativa B
I. Toda função injetora é bijetora. (falsa)
Para ser bijetora, a função tem quer injetora e sobrejetora.
II. Quando elementos diferentes geram imagens diferentes, temos uma função sobrejetora. (falsa)
Essa definição é a de função injetora e não de função sobrejetora.
III. Toda função bijetora admite inversa. (verdadeira)
Uma função é inversível se ela foi bijetora, ou seja, toda função bijetora admite inversa.
VI. Quando a imagem é igual ao contradomínio, temos uma função sobrejetora. (verdadeira)
De fato, a função é sobrejetora se a imagem for igual ao contradomínio da função.
Resposta Questão 9
Alternativa B
Analisando o contradomínio e a imagem, é possível perceber que esses conjuntos possuem os mesmos elementos, logo, essa função é sobrejetora. Por outro lado, existem elementos do domínio que possuem mesma imagem no contradomínio, que são os elementos {-1, 1}, logo, essa função não é injetora e, consequentemente, não é bijetora. Então podemos classificá-la como sobrejetora.
Resposta Questão 10
Alternativa E
Por definição, a função é sobrejetora se o contradomínio for igual ao conjunto imagem.
Resposta Questão 11
Alternativa A
I. \(f:\ \mathbb{R}\rightarrow\mathbb{R}\ |\ f(x)=ax+b \) (é sobrejetora)
Nesse caso sabemos que a função do 1º grau possui imagem igual ao conjunto dos números reais, pois o seu gráfico é sempre uma reta.
II. f: \(\ f:\ \mathbb{R}\rightarrow\mathbb{R}\ |f\left(x\right)=-2x^2\) (não é sobrejetora)
A função quadrática com contradomínio no conjunto dos números reais não pode ser sobrejetora, pois a sua imagem nesse caso sempre será negativa, logo, o conjunto imagem é diferente do contradomínio da função.
III. \(f:\mathbb{R}\rightarrow\mathbb{R}|f\left(x\right)=2^x\) (não é sobrejetora)
A imagem da função exponencial é o conjunto dos números reais positivos, logo, essa função não é sobrejetora.
Resposta Questão 12
Alternativa C
Analisando a função, temos que \(-a\cdot x^2\) sempre gerará um número negativo como resposta, pois \(x^2 \) é sempre positivo. Sabendo que \(a>0\), então \(-a<0\) e o produto de \(-a\) por x² serão sempre um número negativo, logo, a imagem dessa função é o conjunto dos números reais negativos.



