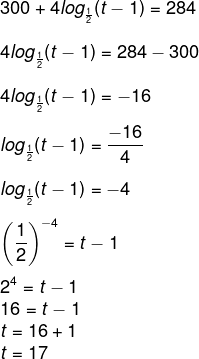Questão 1
Seja f(x) = log2x e g(x) = log3 x a lei de formação de duas funções f(x) e g(x), então o valor de f(8) – g (9) é igual a:
A) 0.
B) 1.
C) 2.
D) –1.
E) – 2.
Questão 2
(Enem 2011) A Escala e Magnitude de Momento (abreviada como MMS e denotada como MW), introduzida em 1979 por Thomas Haks e Hiroo Kanamori, substituiu a Escala de Richter para medir a magnitude dos terremotos em termos de energia liberada. Menos conhecida pelo público, a MMS é, no entanto, a escala usada para estimar as magnitudes de todos os grandes terremotos da atualidade. Assim como a escala Richter, a MMS é uma escala logarítmica. MW e M0 se relacionam pela fórmula:
![]()
Onde M0 é o momento sísmico (usualmente estimado a partir dos registros de movimento da superfície, através dos sismogramas), cuja unidade é o dina⋅cm. O terremoto de Kobe, acontecido no dia 17 de janeiro de 1995, foi um dos terremotos que causaram maior impacto no Japão e na comunidade científica internacional. Teve magnitude MW = 7,3.
Mostrando que é possível determinar a medida por meio de conhecimentos matemáticos, qual foi o momento sísmico M0?
A) 10-5,10
B)10-0,73
C)1012,00
D)1021,65
E)1027,00
Questão 3
Analisando o gráfico da função:
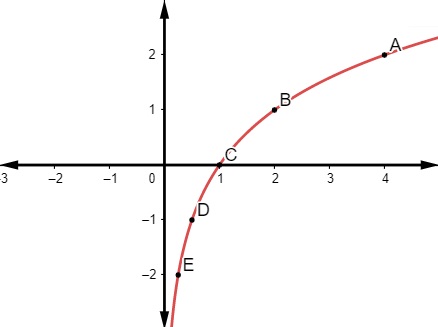
Podemos afirmar que a sua lei de formação é:
A) f(x) = 2x
B) f(x) = logx + 2
C) f(x) = log2x
D)f(x) = – 2x
E) f(x) = log x²
Questão 4
Podemos ver a seguir a representação de uma função logarítmica:
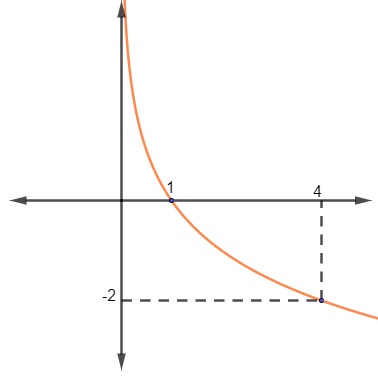
Com base em seu gráfico, sabendo que essa função é uma função do tipo f(x) = logb x, então o valor da base b é:
Questão 5
Sobre a função logarítmica, julgue as afirmativas a seguir:
I → O domínio da função logarítmica é o conjunto dos números reais.
II → A função logarítmica é crescente quando a sua base é maior que 1.
III → A função logarítmica é decrescente quando sua base é negativa.
A) Somente a I é verdadeira.
B) Somente a II é verdadeira.
C) Somente a III é verdadeira.
D) Somente a II e a III são verdadeiras.
E) Somente a I e a II são verdadeiras.
Questão 6
(Uerj) O número, em centenas de indivíduos, de um determinado grupo de animais, x dias após a liberação de um predador no seu ambiente, é expresso pela seguinte função:
![]()
Após cinco dias da liberação do predador, o número de indivíduos desse grupo presentes no ambiente será igual a:
A) 3.
B) 4.
C) 300.
D) 400.
Questão 7
Durante os estudos sobre o crescimento de uma determinada árvore, foi possível modelar o crescimento dela no decorrer do tempo por meio da função A(t) = 1 + log3 (5 + t), em que t é o tempo em anos e A(t) é a altura em metros. Sendo assim, podemos afirmar que altura dessa árvore, após 4 anos, será de:
A) 1 metro.
B) 2 metros.
C) 2 metros e meio.
D) 3 metros.
E) 3 metros e meio.
Questão 8
(UFSM 2009) A partir de dados do Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep), o índice de Desenvolvimento da Educação Básica (Idep) para as séries iniciais do Ensino Fundamental da escola Estadual Básica Professora Margarida Lopes (Santa Maria, RS) pode ser representada pela expressão:
![]()
Considere que f(t) representa o Ideb em função do ano t em que o dado foi coletado. Diante dessas informações, pode-se afirmar que o acréscimo do Ideb previsto para essa escola, de 2005 a 2013, é de:
A) 5
B) 1
C) 1/2
D) 1/4
E) 0
Questão 9
Em uma determinada cidade, o número de nascimentos, no decorrer dos anos, está sempre crescendo. Para compreender melhor essa relação, os matemáticos modelaram uma função que dá a expectativa da quantidade que crianças que vão nascer para um determinado ano.
N(t) = 900 ·log2 (t – 1999)3 , em que t > 1999. De acordo com essa função, supondo que o comportamento seja exatamente o previsto, nascerão 5.400 crianças no ano de:
A) 2002.
B) 2003.
C) 2004.
D) 2005.
E) 2006.
Questão 10
O tempo, em minutos, que um medicamento leva para fazer efeito em uma pessoa é dado pela função:
![]()
Considere que x é a idade e f(x) é o tempo em minutos.
Em um paciente que possui 30 anos, o tempo necessário para que esse remédio faça efeito é de:
(Use log 2 = 0,3.)
A) 2 minutos e 70 segundos.
B) 2 minutos e 42 segundos.
C) 3 minutos e 26 segundos.
D) 5 minutos.
E) 7 minutos e 30 segundos.
Questão 11
(Unesp) A expectativa de vida em anos, em uma região, de uma pessoa que nasceu a partir de 1900 no ano x ( x ≥ 1900) é dada por L(x)=12·(199log10x - 651). Considerando Log2=0,3, uma pessoa dessa região que nasceu no ano 2000 tem expectativa de viver:
A) 48,7 anos.
B) 54,6 anos.
C) 64,5 anos.
D) 68,4 anos.
E) 72,3 anos.
Questão 12
O volume de um reservatório em função do tempo é dado em litros pela função:
![]()
Considere que t ≥ 1, e t é dado em dias e V(t) é dado em litros. Sendo assim, após quantos dias o volume da piscina será de 284 litros?
A) 12 dias
B) 14 dias
C) 15 dias
D) 16 dias
E) 17 dias
Resposta Questão 1
Alternativa B.
Calculando f(8), temos que:
f(8) = log2 8
f(8) = 3
Agora calculando g(9):
g(9) = log39
g(9) = 2
Por fim, a diferença entre elas é 3 – 2 = 1.
Resposta Questão 2
Alternativa E.
Como Mw = 7,3, substituindo na lei de formação, temos que:
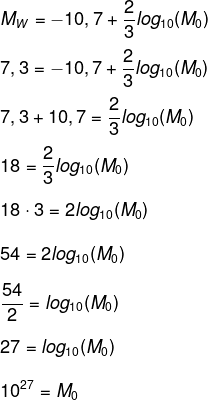
Resposta Questão 3
Alternativa C.
Analisando o comportamento da função, ela é uma função logarítmica. Note que o ponto (2,1) pertence ao gráfico, então:
f(x) = logax
f(2) = loga2
1 = loga2
Aplicando a definição de logaritmo, temos que:
a1= 2
a = 2
Como a base é 2, então a função é:
f(x) = log2x
Resposta Questão 4
Alternativa E.
Analisando o gráfico, sabemos que f(4) = – 2. Então, temos que:
f(4) = logb 4
– 2 = logb 4
Aplicando a definição de logaritmo:
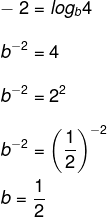
Resposta Questão 5
Alternativa B.
I → Falsa, pois o domínio é formado pelos números reais positivos.
II → Verdadeira. Se a base é maior que 1, a função é crescente.
III → Falsa. A base não pode ser negativa. Para que a função seja decrescente, sua base precisa ser um número maior que 0 e menor que 1.
Resposta Questão 6
Alternativa C.
Calculando f(5), temos que:
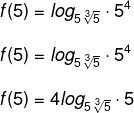
Agora resolvendo o logaritmo, temos que:
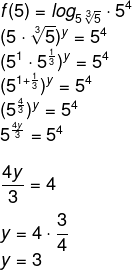
O valor encontrado está em centenas de pessoas, logo há 3 centenas, ou seja, 300.
Resposta Questão 7
Alternativa D.
A(t) = 1 + log3 (5 + t)
A(4) = 1 + log3 (5 + 4)
A(4) = 1 + log3 (9)
A(4) = 1 + 2
A(4) = 3 metros
Resposta Questão 8
Alternativa B
Queremos encontrar a diferença: f(2013) – f(2005).
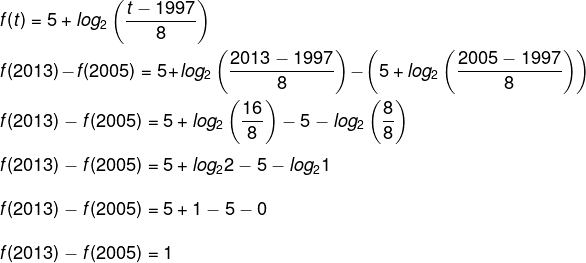
Resposta Questão 9
Alternativa B.
Dada a função:
N(t) = 900 ·log2 (t – 1999)3
Queremos que:
900 ·log2 (t – 1999)3 = 5400
Utilizando a propriedade do logaritmo:
900 ·3 log2 (t – 1999) = 5400
2700 log2 (t – 1999) = 5400
log2(t – 1999) = 5400 : 2700
log2 (t – 1999) = 2
Utilizando a definição de logaritmo:
2² = t – 1999
4 = t – 1999
4 + 1999 = t
2003 = t
Resposta Questão 10
Alternativa B.
Calculando f(30):
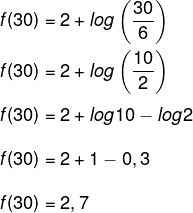
Agora vamos converter a parte decimal em segundos. Sabemos que 0,7 · 60 = 42, ou seja, 2 minutos e 42 segundos.
Resposta Questão 11
Alternativa D.
L(x)=12·(199log10x – 651)
L(2000)=12·(199log102000 - 651)
L(2000)=12·[199log10(1000·2) - 651]
L(2000)=12·[199(log101000+ log102) - 651]
L(2000)=12·[199·(3+ 0,3) - 651]
L(2000)=12·[199·(3,3) - 651]
L(2000)=12·[656,7 - 651]
L(2000)=12·5,7
L(2000) = 68,4 anos