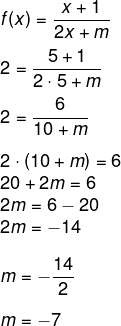Questão 1
Dada a função f: R → R, com lei de formação igual a f(x) = 2x + 1, e seja f-1 sua função inversa, o valor de f- -1 (7) é:
A) 0.
B) 1.
C) 2.
D) 3.
E) 4.
Questão 2
Suponha que a função f seja inversível e que sua lei de formação seja f(x) = 5x – 10. A lei de formação da sua inversa é:
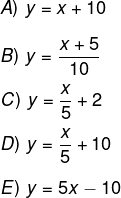
Questão 3
Dada a função com domínio e contradomínio no conjunto dos números reais e lei de formação f(x) = 2x – 5. Sabendo que f-1 é sua inversa, o ponto a seguir que pertence ao gráfico de f-1 é:
A) A(1, – 3).
B) B(4, 5).
C) C(2,1).
D) D(1,3).
Questão 4
(Consulpan) A função inversa de uma função f(x) do 1º grau passa pelos pontos (2, 5) e (3, 0). A raiz de f(x) é:
A) 2
B) 9
C) 12
D) 15
Questão 5
Dada a função f(x) = log2 (x+3) – 2, suponha que ela seja uma função inversível. Desse modo, a lei de formação da sua função inversa é:
A) f-1(x) = 2x – 2 – 3
B) f-1(x) = 2x+3 +2
C) f-1(x) = 3x – 2
D) f-1(x) = log3 (x – 2)
E) f-1(x) = (x+3)² + 2
Questão 6
Dada a função f: A → B, em que A ={0,1, 2, 3} e B{ – 1, 0, 3, 8}, com lei de formação f(x) = x² – 1, podemos afirmar que:
A) a função é inversível, pois ela é bijetora.
B) a função não é inversível, pois ela é injetora, mas não é sobrejetora.
C) a função não é inversível, pois ela é sobrejetora, mas não é injetora.
D) a função não é inversível, pois ela é bijetora.
Questão 7
Sabendo que a função f: A → B, com lei de formação f(x) = x3 + 2, é inversível, então a lei de formação da função inversa é:
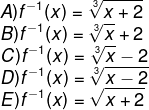
Questão 8
(UEL) Sendo f: R → R+* a função definida por f(x) = 2x, então a expressão que define a função inversa de f é:
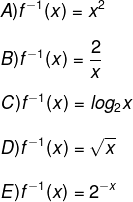
Questão 9
Dada a função bijetora f(x) = 2x – 4, o valor de f( f – 1 (2)) é:
A) – 2
B) – 1
C) 0
D) 1
E) 2
Questão 10
Dada a função f: A → B, em que A= {-1, 0, 1} e B= {0, 1}, com lei de formação f(x)= x², podemos afirmar que:
I → a função é injetora;
II → a função é sobrejetora;
III → a função é bijetora.
É(são) verdadeira(s):
A) somente as afirmativas I e II.
B) somente a afirmativa I.
C) somente a afirmativa II.
D) nenhuma das afirmativas.
E) todas as afirmativas.
Questão 11
(FGV) Considere a função real f definida por:
![]()
e sua inversa f- – 1. Se f –1 (2) = 5, o valor de m é:
A) – 3.
B) – 5.
C) – 7.
D) – 9.
E) – 11.
Questão 12
(UERN) Considerando as funções f(x) 3x – 2 e g(x) – 2x + 1, o valor de k, tal que f(g(k)) – 1 = 1, é:
A) 3.
B) 2.
C) – 1.
D) – 5.
Resposta Questão 1
Alternativa D.
Primeiro encontraremos a lei de formação da função inversa de f. Para isso, trocaremos x por y e f(x) por x na lei de formação:
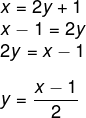
Agora calcularemos o valor numérico para a função quando x = 7:
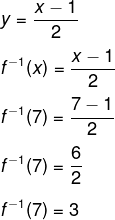
Resposta Questão 2
Alternativa C.
Dada a função f(x) = 5x – 10, para encontrar a sua inversa, vamos substituir x por y e f(x) por x. Então, temos que:
x = 5y – 10
Isolando o y:
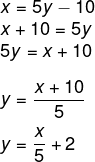
Resposta Questão 3
Alternativa D.
Dado o ponto do tipo (b,a), se ele pertence à função inversa de f(x), então o ponto (a,b) pertence à função f (x).
Para verificar à qual ponto pertence a inversa, basta calcular o valor numérico invertendo os valores do par ordenado.
-
A ( 1, – 3) — se ele pertencer à inversa, então o ponto (– 3,1) pertencerá à f(x). Verificando, temos que:
f (x) = 2x – 5
x = – 3 e y = 1
f( – 3) = 2 · (– 3) – 5
f( – 3) = – 6 – 5 = – 11
Note que o resultado tinha que ser 1, logo o ponto A não pertence à função inversa.
-
B (4,5) — se ele pertencer à inversa, então o ponto (5,4) pertencerá à f(x):
f(5) = 2 · 5 – 5
f(5) = 10 – 5 = 5
Note que o resultado tinha que dar 4, logo o ponto não pertence à inversa de f.
-
C (2,1) → (1,2) pertence à f(x):
f(1) = 2 · 1 – 5
f(1) = 2 – 5
f(1) = – 3
O ponto C não pertence à função inversa, pois o resultado tinha que ser 2.
-
D (1,3) → (3,1) pertence à f(x):
f(3) = 2 · 3 – 5
f(3) = 6 – 5
f(3) = 1
Nesse caso, o ponto (3,1) pertence à f(x), logo o ponto D(1,3) pertence à inversa de f(x).
Resposta Questão 4
Se a função f- – 1(x) passa pelos pontos (2,5) e (3,0), a função f-(x) passa pelos pontos (5,2) e (0,3). Com isso, podemos encontrar a lei de formação da função.
Sabemos que y = ax + b e usando o segundo ponto (0,3), temos que x = 0 e y = 3.
3 = 0 · x + b
3 = b
b = 3
Então:
y = ax + 3
Conhecendo o valor de b, é possível encontrar o valor de a usando o ponto (5,2):
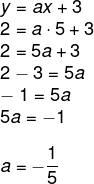
Logo, a lei de formação da função é:
![]()
Agora encontraremos o zero dessa função:
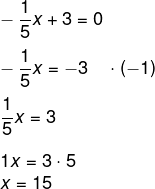
Resposta Questão 5
Alternativa A.
Para encontrar a função inversa, trocaremos f(x) por x e x por y na lei de formação:
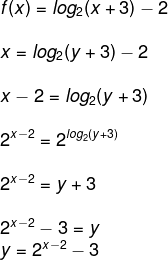
Por fim, basta trocar y por f – 1 (x):
f-1(x) = 2x – 2 – 3
Resposta Questão 6
Alternativa A.
Verificaremos se a função é injetora e sobrejetora.
A sua lei de formação é f(x) = x² – 1. Primeiro verificaremos se ela é injetora. Para isso, calcularemos o valor numérico da função para os valores do domínio A.
f(0) = 0² – 1 = – 1
f(1) = 1² – 1 = 1 – 1 = 0
f(2) = 2² – 1 = 4 – 1 = 3
f(3) = 3² – 1 = 9 – 1 = 8
Note que elementos distintos possuem imagem distinta, logo a função é injetora.
Agora vamos verificar se a função é sobrejetora. Para isso, não pode sobrar nenhum elemento no conjunto B. Note que isso também acontece, pois todo elemento do contradomínio B é imagem de um elemento no conjunto A, então a função é bijetora, logo ela é inversível.
Resposta Questão 7
Alternativa D.
Trocando f(x) por x e x por y, temos que:
x = y3 + 2
Isolando o y:
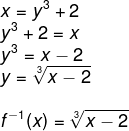
Resposta Questão 8
Alternativa C.
A lei de formação é:
y = 2x
Trocando x por y:
x = 2y
Aplicando logaritmo dos dois lados:
log2x = log22y
log2x = ylog22
log2x = y · 1
log2x = y
y = log2x
f – 1 (x) = log2x
Resposta Questão 9
Alternativa E.
Seja x um número tal que f(x) = 2, então sabemos que f – 1(2) = x. Igualando f(x) a 2, temos que:
2x – 4 = 2
2x = 2 + 4
2x = 6
x = 6 : 2
x = 3
Sabemos que f(3) = 2 → f – 1 (2) = 3, logo f( f – 1 (2)) = f(3), mas sabemos que f(3) = 2, então:
f( f – 1 (2)) = 2
Resposta Questão 10
Alternativa C.
I – Falsa.
Verificando se a função é injetora, temos que:
f( – 1) = ( – 1)² = 1
f(0) = 0² = 0
f(1) = 1² = 1
Note que a função não é injetora, pois f( – 1) = f(1).
II – Verdadeira.
Para todo elemento b do contradomínio B {0,1}, existe pelo menos um elemento no domínio tal que f(a) = b, logo a função é sobrejetora.
III – Falsa.
Como a função não é injetora, ela não pode ser bijetora.
Resposta Questão 12
Alternativa D.
Primeiro encontraremos a função f(g(x)):
f(g(x)) = 3 (-2x + 1) - 2
f(g(x)) = -6x + 3 - 2
f(g(x)) = -6x + 1
Sabemos que f(g(k)) – 1 = 1, então f(g(1)) = k. Como queremos o valor de k, temos que:
f(g(x)) = -6x + 1
x = 1 e f(g(1)) = k
k = – 6· 1 + 1
k = – 6 + 1
k = – 5