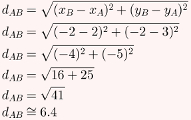Questão 1
Qual é a distância entre os pontos A e B, em centímetros, sabendo que suas coordenadas são A = (2,3) e B = (-2,-2)?
a) 41 cm
b) 6 cm
c) 49 cm
d) 41,5 cm
e) 6,4 cm
Questão 2
Determine a área, em metros quadrados, do triângulo a seguir, sabendo que ele é retângulo em B.
.jpg)
Triângulo retângulo em B
a) 2 m2
b) 5,66 m2
c) 2,83 m2
d) 8 m2
e) 9 m2
Questão 3
(Cesgranrio) A área do triângulo, cujos vértices são (1, 2), (3, 4) e (4, -1), é igual a:
a) 6.
b) 8.
c) 9.
d) 10.
e) 12.
Questão 4
(PUC) O ponto B = (3, b) é equidistante dos pontos A = (6, 0) e C = (0, 6). Logo, o ponto B é:
a) (3, 1).
b) (3, 6).
c) (3, 3).
d) (3, 2).
e) (3, 0).
Resposta Questão 1
Resposta Questão 2
Calcule as distâncias entre B e C (dBC) e entre B e A (dBA), que são a base e a altura desse triângulo, uma vez que ele é retângulo em B.
Primeiramente, calcularemos dBC:
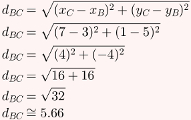
Agora, calcularemos dBA:
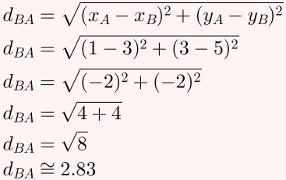
Para finalizar o exercício, basta calcular a área desse triângulo, lembrando que a área de um triângulo pode ser calculada multiplicando sua base por sua altura e dividindo o resultado por 2:
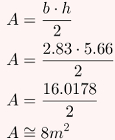
Gabarito: Letra D.
Resposta Questão 3
Primeiro, desenharemos o triângulo e mostraremos que um de seus ângulos é reto. Caso um dos ângulos do triângulo não seja reto, é necessário descobrir sua altura, o que pode ser feito utilizando distância entre ponto e reta.
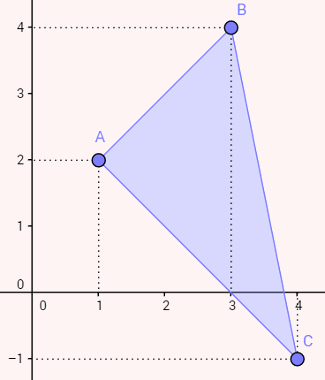
Observe que possivelmente o ângulo A é um ângulo reto. Caso isso ocorra, AB já é a altura do triângulo com relação à base AC. Para garantir isso, basta calcular os coeficientes angulares de AB e de AC. Caso o coeficiente angular de AB seja o “inverso do oposto” do coeficiente angular de AC, então AC e AB são perpendiculares e A é um ângulo reto.
Primeiramente, o coeficiente angular de AC:
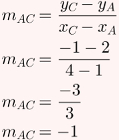
Agora, o coeficiente angular de AB:
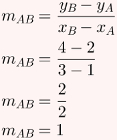
Os coeficientes angulares são inversos e opostos. Logo, AC é perpendicular a AB. Assim, AB é a altura do triângulo ABC, enquanto AC é a base. Para calcular a área desse triângulo, é necessário calcular antes os comprimentos de sua base e altura, que são os segmentos perpendiculares AC e AB. Para tanto, utilizaremos a fórmula da distância entre dois pontos. Observe:
Cálculo da altura do triângulo ABC:
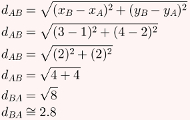
Cálculo da base do triângulo ABC:
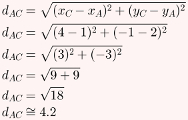
Agora, basta calcular a área do triângulo ABC, sabendo que sua base mede aproximadamente 4,2 e sua altura mede aproximadamente 2,8.
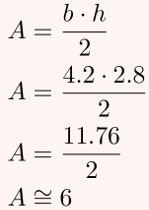
Como os valores das distâncias foram arredondados para baixo, então o valor obtido na área é um pouco menor que 6. Logo, conforme as alternativas de resposta, a área desse triângulo é 6.
Gabarito: Letra A.
Resposta Questão 4
Para resolver esse exercício, basta resolver a equação dAB = dBC. Antes disso, porém, calcularemos dAB e dBC separadamente e elevaremos seus resultados ao quadrado. Primeiramente, a distância entre A e B:
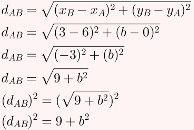
Agora, a distância entre B e C:
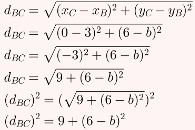
O resultado final é obtido resolvendo a equação gerada por (dAB)2 = (dBC)2. Observe:
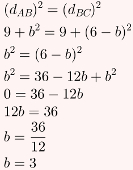
Gabarito: Letra C.