Questão 1
Após a aula de matemática sobre corpos redondos, Kárita resolveu anotar as formas geométricas que ela via em seu cotidiano e que poderiam ser classificadas como corpos redondos. Ao final do dia, em suas anotações, constavam os seguintes sólidos:
Tronco de cone – Hemisfério – Círculo – Cilindro – Cone
Das formas geométricas listadas, a que não pode ser classificada como um corpo redondo é:
A) tronco de cone
B) hemisfério
C) círculo
D) cilindro
E) cone
Questão 2
Um recipiente esférico de raio medindo 5 cm será confeccionado utilizando plástico. Sabendo que esse recipiente será oco por dentro e desprezando a sua espessura, qual será a área total de plástico dele?
(Use π = 3)
A) 75 cm²
B) 150 cm²
C) 300 cm²
D) 500 cm²
E) 1500 cm²
Questão 3
Natália decidiu comprar um novo vaso para a sua samambaia. Ao chegar à loja, o modelo de vaso disponível tinha o formato do sólido abaixo:
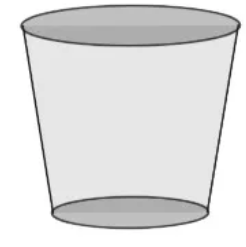
Quando ela chegou em casa, sua filha, muito curiosa, perguntou-lhe qual era o nome do formato geométrico do vaso. Ao analisarmos a forma do vaso, podemos afirmar que ele é um/uma:
A) esfera
B) cilindro
C) cone
D) hemisfério
E) tronco de cone
Questão 4
Uma cisterna cilíndrica possui 2 metros de diâmetro. O seu volume foi medido, e constatou-se que ela estava com 40% da sua capacidade, guardando 4,8 m³ de água. Nessas condições, podemos afirmar que a altura dessa cisterna é:
(Use π=3)
A) 1 metro
B) 2 metros
C) 3 metros
D) 4 metros
E) 5 metros
Questão 5
Analisando as bolas utilizadas no campeonato brasileiro, percebeu-se que existem diferentes medidas de raio de uma bola para outra. Durante a análise, foi possível encontrar bolas com raio de, no mínimo, 10 centímetros, e, no máximo, 13 centímetros. Utilizando π=3, podemos afirmar que a diferença entre o volume da maior bola e o volume da menor bola é:
A) 2143 cm³
B) 3365 cm³
C) 5424 cm³
D) 8788 cm³
Questão 6
Um recipiente possui formato de um cone, com altura de 30 cm e diâmetro de 24 cm. O volume desse recipiente é:
(Use π=3,1)
A) 62,9 cm³
B) 74,4 cm³
C) 111,6 cm³
D) 148,8 cm³
E) 297,6 cm³
Questão 7
A piscina da casa de Marcelo será construída de modo que ela tenha 2,5 metros de raio. Utilizando 3,1 como aproximação para π, qual deve ser a altura dessa piscina para que a sua capacidade quando estiver totalmente cheia seja de 19.375 litros?
A) 1,0 metro
B) 1,5 metros
C) 2,0 metros
D) 2,5 metros
E) 3,0 metros
Questão 8
Sobre os sólidos geométricos, podemos afirmar que:
I. Os sólidos geométricos são divididos em dois grandes grupos, os poliedros e os corpos redondos.
II. O cilindro é um caso de prisma de base circular, por exemplo.
III. O cone e a esfera são exemplos de corpos redondos.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa
D) Todas as afirmativas são verdadeiras.
Questão 9
(Enem) Um arquiteto está fazendo um projeto de iluminação de ambiente e necessita saber a altura que deverá instalar a luminária ilustrada na figura.
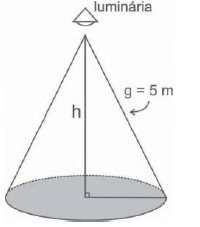
Sabendo que a luminária deverá iluminar uma área circular de 28,26 m², e considerando π ≅ 3,14, a altura h será igual a
A) 3 m.
B) 4 m.
C) 5 m.
D) 9 m.
E) 16 m.
Questão 10
(Enem) Uma loja de materiais de construção vende dois tipos de caixas-d’água: tipo A e tipo B. Ambas têm formato cilíndrico e possuem o mesmo volume, e a altura da caixa-d’água do tipo B é igual a 25% da altura da caixa-d’água do tipo A. Se R denota o raio da caixa-d’água do tipo A, então o raio da caixa-d’água do tipo B é
A) R2
B) 2R
C) 4R
D) 5R
E) 16R
Questão 11
(Enem) Uma empresa que organiza eventos de formatura confecciona canudos de diplomas a partir de folhas de papel quadradas. Para que todos os canudos fiquem idênticos, cada folha é enrolada em torno de um cilindro de madeira de diâmetro d em centímetros, sem folga, dando-se 5 voltas completas em torno de tal cilindro. Ao final, amarra-se um cordão no meio do diploma, bem ajustado, para que não ocorra o desenrolamento, como ilustrado na figura:
Em seguida, retira-se o cilindro de madeira do meio do papel enrolado, finalizando a confecção do diploma. Considere que a espessura da folha de papel original seja desprezível. Qual é a medida, em centímetros, do lado da folha de papel usado na confecção do diploma?
A) π d
B) 2π d
C) 4π d
D) 5π d
E) 10π d
Questão 12
(Enem) Em um casamento, os donos da festa serviam champanhe aos seus convidados em taças com formato de um hemisfério (Figura 1), porém um acidente na cozinha culminou na quebra de grande parte desses recipientes. Para substituir as taças quebradas, utilizou-se um outro tipo com formato de cone (Figura 2). No entanto, os noivos solicitaram que o volume de champanhe nos dois tipos de taças fosse igual.
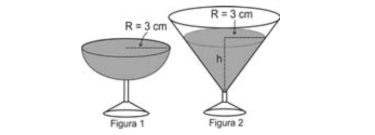
Considere:
Vesfera= 43πR3 e Vcone= 13πR2h
Sabendo que a taça com o formato de hemisfério é servida completamente cheia, a altura do volume de champanhe que deve ser colocado na outra taça, em centímetros, é de
A) 1,33
B) 6,00
C) 12,00
D) 56,52
E) 113,04
Resposta Questão 1
Alternativa C
O círculo não é um objeto bidimensional, sendo assim, ele não pode ser classificado como um corpo redondo.
Resposta Questão 2
Alternativa C
Calculando a área total da esfera de raio 5 cm, temos que:
AT=4πr2
AT=4⋅3⋅52
AT=12⋅25
AT=300 cm²
Resposta Questão 3
Alternativa E
Podemos perceber que esse sólido geométrico possui duas bases circulares de raios diferentes. Característica essa de um tronco de cone, que pode ser obtido quando fazemos uma secção transversal no cone.
Resposta Questão 4
Alternativa D
Sabemos que o volume de um cilindro é calculado por V=πr2h. Como o diâmetro é de 2 metros, então o raio mede 1 metro. Além disso, sabemos que 40% do volume são 48, então 0,4V=4,8. Assim temos que:
0,4V=0,4πr2h
4,8=0,4⋅3⋅12⋅h
4,8=1,2⋅1⋅h
4,8=1,2h
h=4,81,2
h=4
Resposta Questão 5
Alternativa B
Calculando o volume máximo VM e o volume mínimo Vm:
Vm=43πr3
Vm=43⋅3⋅113
Vm=4⋅113
Vm=5324
Calculando VM:
VM=43⋅3⋅133
VM=4⋅133
VM=8788
Então a diferença entre o volume máximo e o volume mínimo é:
VM−Vm=8788−5424=3365 cm3
Resposta Questão 6
Alternativa D
Calculando o volume do cone, temos que:
V=πr23
V=3,1⋅1223
V=3,1⋅1443
V=3,1⋅48
V=148,8 cm3
Resposta Questão 7
Alternativa A
Sabemos que:
V=πr2h
Se o volume é de 19.375 litros, então, em m³, temos que:
19.375∶1000=19,375 m3
Utilizando π=3,1 e r=2,5, temos que:
19,375=3,1⋅2,52⋅h
19,375=3,1⋅6,25⋅h
19,375=19,375h
h=19,37519,375
h=1 m
Resposta Questão 8
Alternativa B
I. Os sólidos geométricos são divididos em dois grandes grupos, os poliedros e os corpos redondos. (Verdadeiro)
II. O cilindro é um caso de prisma de base circular, por exemplo. (Falso)
O cilindro não pode ser considerado um prisma, pois o prisma possui base formada por polígono, já que é um poliedro; o cilindro, por sua vez, possui base circular, o que faz com que ele seja um corpo redondo.
III. O cone e a esfera são exemplos de corpos redondos. (Verdadeiro)
Resposta Questão 9
Alternativa B
Sabemos que a área da base é formada por um círculo, então temos que:
Ab=πr2
πr2=28,26
3,14r2=28,26
r2=28,263,14
r2=9
r=√9
r= 3
Conhecendo a medida do raio, para encontrar a altura, utilizaremos o teorema de Pitágoras:
g2=r2+h2
52=32+h2
25=9+h2
25−9=h2
16=h2
h=√16
h=4
Resposta Questão 10
Alternativa B
Sabemos que a altura do cilindro B é 25% da altura do cilindro A:
hb=0,25hA
Como os volumes são iguais, temos que:
πR2ha=πr2hb
Então temos que:
R2ha=r20,25ha
R2=r20,25
R=√0,25r2
R=0,5r
R=12r
2R=r
Resposta Questão 11
Alternativa D
O diploma possui formato de um cilindro cujo comprimento da circunferência é calculado por:
C=2πr
Sabemos que foram dadas 5 voltas, então temos que:
5C=5⋅2 πr
Como o raio é igual à metade do diâmetro:
r=d2
5C=5⋅2πd2
5C=5⋅π⋅d
Então a medida, em centímetros, do lado da folha de papel usado na confecção do diploma é:
5π d cm
Resposta Questão 12
Alternativa B
Sabemos que o hemisfério é metade da esfera, então, utilizando o volume da esfera, temos que:
Vh=43πr3:2
Vh=46πr3
Vh=46⋅π⋅33
Vh=46⋅π⋅27
Vh=18π
Calculando o volume do cone:
Vc=πr2h3
Vc=π⋅32⋅h3
Vc=3πh
Vh=Vc
18π=3πh
h=18π3π
h=6
RECOMENDADOS PARA VOCÊ
Ferramentas Brasil Escola
