Questão 1
Analise a planificação a seguir:
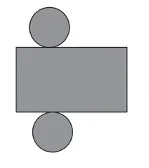
O sólido geométrico que pode ser formado com essa planificação é conhecido como:
A) prisma de base circular
B) tronco de um cone
C) cone
D) cilindro
E) paralelepípedo redondo
Questão 2
Sobre o cilindro, julgue as afirmativas a seguir:
I – O cilindro não pode ser considerado um poliedro.
II – A planificação do cilindro é composta por um arco e um círculo.
III – O cilindro é um prisma de base circular.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são falsas.
Questão 3
Para preencher um recipiente cilíndrico de areia, que possui raio r e altura h, será utilizado um copo no formato de um cone, com raio r e altura h iguais aos do cilindro. Quantas vezes, no mínimo, é necessário preencher o copo e despejar no cilindro para encher todo este recipiente?
A) 2 vezes
B) 3 vezes
C) 4 vezes
D) 5 vezes
E) 6 vezes
Questão 4
Uma cisterna possui formato de um cilindro, com raio medindo 3 metros e altura igual a 5 metros. Sabendo que \(\frac{2}{5}\) dessa cisterna está ocupada, a quantidade restante do volume, que não está ocupada, mede: (use π=3)
A) 54 m³
B) 63 m³
C) 76 m³
D) 81 m³
E) 135 m³
Questão 5
Qual é a medida do raio de um cilindro que possui volume igual a 120 m³, sabendo que a sua altura é de 10 metros e utilizando 3 como aproximação para π ?
A) 2 m
B) 3 m
C) 4 m
D) 5 m
E) 6 m
Questão 6
(Enem 2015) Para resolver o problema de abastecimento de água foi decidida, numa reunião do condomínio, a construção de uma nova cisterna. A cisterna atual tem formato cilíndrico, com 3 m de altura e 2 m de diâmetro, e estimou-se que a nova cisterna deverá comportar 81 m³ de água, mantendo o formato cilíndrico e a altura da atual. Após a inauguração da nova cisterna, a antiga será desativada.
Utilize 3,0 como aproximação para π.
Qual deve ser o aumento, em metros, no raio da cisterna para atingir o volume desejado?
A) 0,5
B) 1,0
C) 2,0
D) 3,5
E) 8,0
Questão 7
(Enem 2015) O índice pluviométrico é utilizado para mensurar a precipitação da água da chuva, em milímetros, em determinado período de tempo. Seu cálculo é feito de acordo com o nível de água da chuva acumulada em 1 m², ou seja, se o índice for de 10 mm, significa que a altura do nível de água acumulada em um tanque aberto, em formato de um cubo com 1 m² de área de base, é de 10 mm. Em uma região, após um forte temporal, verificou-se que a quantidade de chuva acumulada em uma lata de formato cilíndrico, com raio 300 mm e altura 1 200 mm, era de um terço da sua capacidade.
Utilize 3,0 como aproximação para π.
O índice pluviométrico da região, durante o período do temporal, em milímetros, é de
A) 10,8.
B) 12,0.
C) 32,4.
D) 108,0.
E) 324,0.
Questão 8
(Enem 2022) Peças metálicas de aeronaves abandonadas em aeroportos serão recicladas. Uma dessas peças é maciça e tem o formato cilíndrico, com a medida do raio da base igual a 4 cm e a da altura igual a 50 cm. Ela será derretida, e o volume de metal resultante será utilizado para a fabricação de esferas maciças com diâmetro de 1 cm, a serem usadas para confeccionar rolamentos. Para estimar a quantidade de esferas que poderão ser produzidas a partir de cada uma das peças cilíndricas, admite-se que não ocorre perda de material durante processo de derretimento.
Quantas dessas esferas poderão ser obtidas por meio de cada peça cilíndrica?
A) 800
B) 1200
C) 2400
D) 4800
E) 6400
Questão 9
(Enem 2010) Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.
Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
A) encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
B) encher a leiteira toda de água, pois ela tem um volume 20 vezes maior que o volume do copo.
C) encher a leiteira toda de água, pois ela tem um volume 10 vezes maior que o volume do copo.
D) encher duas leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
E) encher cinco leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
Questão 10
Um recipiente será confeccionado no formato de um cilindro, contendo 1 metro de raio e 0,5 metro de altura. Utilizando 3,1 como aproximação de π , a área total desse recipiente está
A) entre 6 m² e 7 m²
B) entre 7 m² e 8 m²
C) entre 8 m² e 9 m²
D) entre 9 m² e 10 m²
E) entre 10 m² e 11 m²
Questão 11
Com o objetivo de descobrir o volume de um metal precioso encontrado em um local de mineração, um recipiente cilíndrico, com 12 cm de raio e 20 cm de altura, foi preenchido com água, até chegar a uma altura de 10 cm. Posteriormente, foi colocado o metal precioso todo submerso nesse recipiente, aumentando a altura da água para 14 cm. Utilizando π=3 , o volume desse metal precioso é de:
A) 1728 cm³
B) 1546 cm³
C) 1112 cm³
D) 940 cm³
E) 864 cm³
Questão 12
Um cilindro possui volume igual a 1538,6 cm³. Se o diâmetro desse cilindro é de 14 cm e π=3,14 , a altura desse cilindro é de
A) 9 cm
B) 10 cm
C) 11 cm
D) 12 cm
E) 13 cm
Resposta Questão 1
Resposta Questão 2
Alternativa A
I - Verdadeira. De fato, o cilindro é classificado como corpo redondo, portanto ele não pode ser considerado um poliedro.
II - Falsa. A planificação do cilindro possui um retângulo e dois círculos.
III - Falsa. O cilindro não é um prisma, pois os prismas possuem polígonos em suas bases, e o círculo não é um polígono.
Resposta Questão 3
Alternativa B
Sabemos que o volume do cilindro é dado por \(V=\pi r^2h\) e que o volume do cone é \(V=\frac{\pi r^2h}{3}\).
Note, então, que o volume do cilindro é igual ao triplo do volume do cone, sendo necessário utilizar o copo cônico 3 vezes para preencher o recipiente cilíndrico.
Resposta Questão 4
Alternativa D
Calculando o volume da cisterna, temos que:
\(V=\pi r^2\cdot h\)
\(V=3\cdot3^2\cdot5\)
\(V=3\ \cdot9\ \cdot5\)
\(V=27\cdot5\)
\(V=135{\ m}^3\)
Sabendo que a capacidade é de 135 m³, calculando \(\frac{2}{5}\) , temos que:
\(135\cdot\frac{2}{5}=\frac{270}{5}=54\)
Se 54 m³ estão preenchidos, restará então um total de:
\(135-54=81{\ m}^3\)
Resposta Questão 5
Alternativa B
Calculando o volume, temos que:
\(V=\pi\cdot r^2\cdot h\)
Substituindo os valores conhecidos:
\(120=3\cdot r^2\cdot10\)
\(120=30r^2\)
\(\frac{120}{30}=r^2\)
\(4=r^2\)
\(r=\sqrt4\)
\(r=2\)
O raio é de 2 metros.
Resposta Questão 6
Alternativa B
A nova cisterna e a antiga possuem 3 m de altura. Sendo r o raio da nova cisterna com volume de 81 m³, temos que:
\(V=81\ \)
\(\pi r^2h=81\)
\(3r^2\cdot3=81\)
\(9r^2=81\)
\(r^2=\frac{81}{9}\)
\(r^2=9\)
\(r=\sqrt9\)
\(r=3\)
Ao comparar as cisternas, percebemos que a cisterna anterior tinha 2 metros de raio, e a nova tem 3 metros, a diferença então é de 3 – 2 = 1 metro.
Resposta Questão 7
Alternativa D
Sabemos que o volume acumulado na lata é de 1/3 da sua capacidade. Calculando o volume da lata:
\(V=(\pi r^2h)\)
\(V=3\cdot{300}^2\cdot1.200\)
\(V=3\ \cdot900.000\ \cdot1.200\)
\(V=324.000.000\)
Agora, dividindo por 3, já que somente 1/3 da sua capacidade possui água:
\(V:3=324.000.000∶3\ \)
\(V:3=108.000.000\ mm^3\)
Conhecendo o volume da lata, temos que a quantidade de água acumulada no cubo deve ter o mesmo volume. Sendo h a altura da água e sabendo que o lado da base mede 1 m, ou seja 1000 mm:
\(h\cdot{1.000}^2=108.000.000\)
\(h\cdot1000000=108.000.000\)
\(h=\frac{108.000.000}{1.000.000}\)
\(h=108,0\ mm\)
Resposta Questão 8
Alternativa D
Calcularemos primeiro o volume do cilindro:
\(V=\pi r^2\cdot h=\pi\cdot4^2\cdot50=800\pi\)
Calculando o volume da esfera:
\(V=\frac{4}{3}\cdot\pi r^3\ \)
\(V=\frac{4}{3}\cdot\pi\cdot{0,5}^3\ \)
\(V=\frac{4}{3}\cdot\left(\frac{1}{2}\right)^3\pi\ \)
\(V=\frac{4}{3}\cdot\frac{1}{8}\pi\ \)
\(V=\frac{4}{24}\pi\ \)
\(V=\frac{1}{6}\pi\)
Calculando a divisão entre o volume do cilindro e o da esfera:
\(800\pi∶\frac{1}{6}\pi=800∶\frac{1}{6}=800\cdot\ \frac{6}{1}=800\cdot6=4800\)
Resposta Questão 9
Alternativa A
Para calcular o volume de 1 copo, temos que:
\(V=\pi r^2h=\pi\cdot2^2\cdot4=16\pi\ cm^3\)
Agora, calculando o volume da chaleira:
\(V=\pi r^2\cdot H=\pi\cdot4^2\cdot20=16\cdot20\ cm^3\)
Perceba que o volume da leiteira é igual a 20 vezes o volume de um copo, logo a leiteira inteira encherá 20 copos. Entretanto, sabemos que os copos serão cheios até a metade. Sendo assim, é necessário encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
Resposta Questão 10
Alternativa D
Calculando a área total do cilindro:
\(A=2\pi r\left(r+h\right)\)
\(A=2\cdot3,1\ \cdot1\ (1+0,5)\)
\(A=6,1\cdot1,5\ \)
\(A=9,15\ m^2\)
9,15 m² está entre 9 m² e 10 m².
Resposta Questão 11
Alternativa A
Para calcular o volume desse metal precioso, calcularemos o volume de água que aumentou no recipiente após o metal ficar submerso na água.
Primeiramente, sabemos que a altura aumentou um total de 4 cm, pois 14 – 10 = 4 cm. Sabendo que o raio é 12 cm:
\(V=\pi r^2h\)
\(V=3\cdot{12}^2\cdot4\)
\(V=\ 3\ \cdot144\ \cdot4\ \)
\(V=1728\ cm^3\)
Resposta Questão 12
Alternativa B
O raio desse cilindro mede a metade do seu diâmetro; 14 : 2 = 7 cm.
Se V = 1538,6, então:
\(1538,6=\pi r^2h\)
\(1538,6=3,14\cdot7^2\cdot h\)
\(\frac{1538,6}{3,14}=49h\)
\(490\ =\ 49h\)
\(h=\frac{490}{49}\)
\(h=\ 10\ cm\)



