Questão 2
Em função de √2, qual é o resultado da expressão a seguir?

a) 22√2
b) 16√2
c) 32√2
d) 21√2
e) 18√2
Questão 3
Quais são as raízes da equação x2 + 16x – 36 = 0?
a) 2 e 3
b) 20 e 20
c) 2 e 20
d) 20 e – 20
e) 2 e – 18
Questão 4
Um lote quadrado possui 1600 m2 de área. Qual é a medida do comprimento desse lote quadrado?
a) 40 m
b) 42 m
c) 44 m
d) 46 m
e) 48 m
Resposta Questão 1
Para calcular essa raiz, utilizaremos o método da fatoração:

Em vez de multiplicar todos os fatores obtidos, como é feito para encontrar o mínimo múltiplo comum, reescreva esses fatores agrupando-os em potências de 3 sempre que possível, como foi feito acima.
Para finalizar, substitua 3375 por 33·53 no radical para obter a seguinte raiz e prossiga utilizando as propriedades dos radicais.
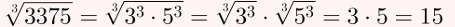
Gabarito: Letra D.
Resposta Questão 2
Primeiramente, decomponha 2048 e 512. Após isso, reescreva os fatores primos em potências de 2, se possível.
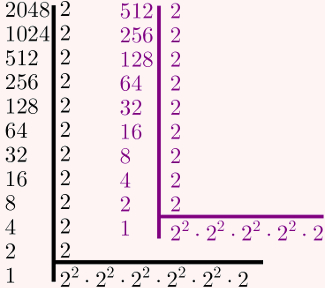
Por fim, utilize as mesmas propriedades do exercício anterior para simplificar os cálculos e subtraia os resultados. Observe:
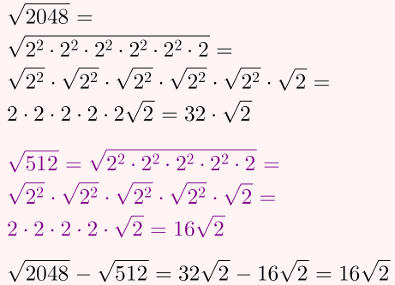
Gabarito: Letra B.
Resposta Questão 3
Utilizando o método de Bhaskara, calcularemos o discriminante:
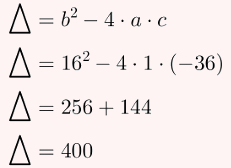
Tendo em vista que precisaremos calcular a raiz de 400 para usar seu resultado na fórmula de Bhaskara, seguem os respectivos cálculos:
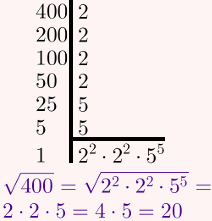
Agora resta apenas calcular as raízes:
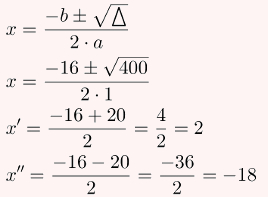
Dessa maneira, as raízes são 2 e –18.
Gabarito: Letra E.
Resposta Questão 4
A medida do lado de um quadrado sempre pode ser obtida a partir da raiz quadrada de sua área. Portanto, basta calcular a raiz quadrada de 1600 para obter a medida em questão. Utilizando o método da fatoração, teremos:
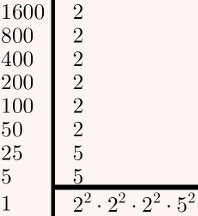
Para finalizar, substitua 1600 no radical pelo produto encontrado na fatoração anterior, como ilustrado na imagem seguinte:

Portanto, o comprimento do lote é 40 m.
Gabarito: Letra A.



