Questão 1
Um triângulo possui base de 12 cm e a altura relativa a essa base igual a 8 cm. A área desse triângulo é igual a:
A) 12 cm².
B) 20 cm².
C) 24 cm².
D) 48 cm².
E) 96 cm².
Questão 2
A seguir temos a representação de uma região limitada por um triângulo:
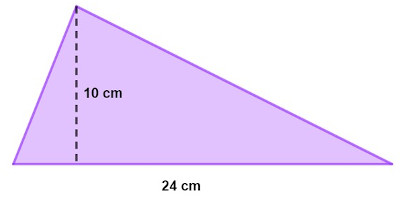
A medida da superfície dessa região é:
A) 34 cm².
B) 68 cm².
C) 84 cm².
D) 120 cm².
E) 210 cm².
Questão 3
Um triângulo é conhecido como equilátero quando ele possui todos os lados congruentes, ou seja, com a mesma medida. A área do triângulo equilátero que possui lado de 6 cm é igual a:
A) 18 cm²
B) \(18\sqrt2\) cm²
C) \(6\sqrt3\) cm²
D) \(16\sqrt2\) cm²
E) \(9\sqrt3\) cm²
Questão 4
Durante uma fiscalização do Ibama, em uma área de desmatamento ilegal na Amazônia, foi encontrada uma região que possui uma área de 64 km² e formato próximo a um triângulo, com base medindo 8 km. Nessas condições, a altura desse triângulo tem que ser de:
A) 128 km.
B) 32 km.
C) 16 km.
D) 12 km.
E) 8 km.
Questão 5
A base de um triângulo é igual à metade da sua altura. Se a sua área é de 36 m², então a medida da sua base é de:
A) 6 metros.
B) 8 metros.
C) 10 metros.
D) 12 metros.
E) 14 metros.
Questão 6
Natália separou uma região em formato de um triângulo equilátero do seu terreno para construir um jardim para a sua filha. Essa região possui área igual a 6,8 m². Utilizando 1,7 como aproximação de \(\sqrt{3}\), qual é a medida do lado desse triângulo?
A) 5 metros.
B) 4 metros.
C) 3 metros.
D) 2 metros.
E) 1 metro.
Questão 7
O perímetro do triângulo a seguir é igual a 61 cm. A área desse terreno mede:
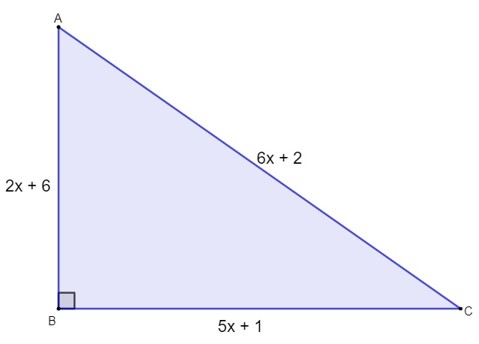
A) 75 cm².
B) 98 cm².
C) 147 cm².
D) 196 cm².
E) 294 cm².
Questão 8
Em terreno com formato de um triângulo retângulo com catetos de 12 metros e 15 metros, foi colocado um tablado quadrado com lados de 3 metros. O restante da área foi todo gramado. Nessas condições, a área gramada desse terreno mede:
A) 90 m².
B) 81 m².
C) 75 m².
D) 69 m².
E) 64 m².
Questão 9
O pai de Thiago deixou de herança para ele e seu irmão dois terrenos de mesma área. O terreno do Thiago é um triângulo, com um dos seus lados medindo 16 metros. O terreno do seu irmão é um retângulo, com lados medindo 24 metros e 8 metros. Então podemos afirmar que a altura relativa ao lado conhecido do terreno de Thiago mede:
A) 8 metros.
B) 12 metros.
C) 16 metros.
D) 18 metros.
E) 24 metros.
Questão 10
Analise a figura plana a seguir:
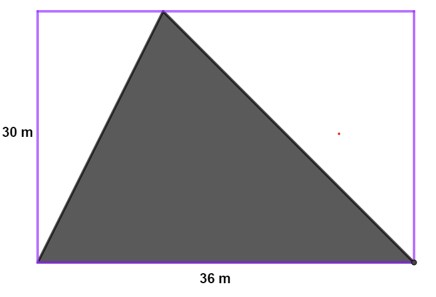
A área da parte branca do retângulo é igual a?
A) 450 m²
B) 490 m²
C) 540 m²
D) 750 m²
E) 1080 m²
Questão 11
A base de um triângulo mede x + 1 e a sua altura mede x – 1. Se a área desse triângulo é igual a 24 m², então o valor de x é:
A) 8.
B) 7.
C) 6.
D) 5.
E) 4.
Questão 12
A área de um triângulo retângulo que possui hipotenusa medindo 25 cm e um dos catetos medindo 20 cm é:
A) 250 cm².
B) 175 cm².
C) 320 cm².
D) 150 cm².
Questão 13
(Enem 2012) Para decorar a fachada de um edifício, um arquiteto projetou a colocação de vitrais compostos de quadrados de lado medindo 1 m, conforme a figura a seguir.
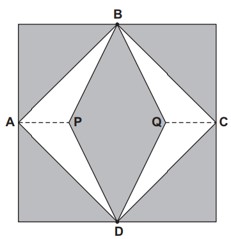
Nesta figura, os pontos A, B, C e D são pontos médios dos lados do quadrado e os segmentos AP e QC medem 1/4 da medida do lado do quadrado. Para confeccionar um vitral, são usados dois tipos de materiais: um para a parte sombreada da figura, que custa R$ 30 o m², e outro para a parte mais clara (regiões ABPDA e BCDQB), que custa R$ 50 o m².
De acordo com esses dados, qual é o custo dos materiais usados na fabricação de um vitral?
A) R$ 22,50
B) R$ 35,00
C) R$ 40,00
D) R$ 42,50
E) R$ 45,00
Resposta Questão 1
Alternativa D.
Calculando a área, temos que:
\(A=\frac{b⋅h}2\)
\(A=\frac{12⋅8}2\)
\(A=\frac{96}2\)
\(A=48\ cm^2\)
Resposta Questão 2
Alternativa D.
A medida da superfície é igual à área do triângulo, que, nesse caso, possui base igual a 24 cm e altura igual a 10 cm.
\(A=\frac{b⋅h}2\)
\(A=\frac{24⋅10}2\)
\(A=\frac{240}2\)
\(A=120\ cm^2\)
Resposta Questão 3
Alternativa E.
A área do triângulo equilátero é calculada pela fórmula:
\(A=\frac{l^2 \sqrt3}4\)
Então, temos que:
\(A=\frac{6^2 \sqrt3}4\)
\(A=\frac{36 \sqrt3}4\)
\(A=9\sqrt3 \ cm^2\)
Resposta Questão 4
Alternativa C.
Como a área é de 64 km², então temos que:
\(A=\frac{b⋅h}2\)
\(64=\frac{8⋅h}2\)
\(64 ⋅2 = 8h\)
\(128 = 8h\)
\(h=\frac{128}8\)
\(h=16\ km\)
Resposta Questão 5
Alternativa A.
Sabemos que a base é igual à metade da altura, logo temos que:
\(b=\frac{h}2\)
\(2b = h\)
Vamos calcular agora a área desse triângulo:
\(A=\frac{b⋅h}2\)
\(36=\frac{b⋅2b}2\)
\(36=\frac{2b^2}2\)
\(36=b^2\)
\(\sqrt{36}=b\)
\(6 = b\)
Então, a base desse triângulo é de 6 metros.
Resposta Questão 6
Alternativa B.
A área do triângulo equilátero é calculada por:
\(A=\frac{l^2 \sqrt3}4\)
Então, temos que:
\(6,8=\frac{l^2\cdot 1,7}4\)
\(6,8⋅4=l^2⋅1,7\)
\(27,2=l^2⋅ 1,7\)
\(\frac{27,2}{1,7}=l^2\)
\(16=l^2\)
\(l=\sqrt{16}\)
\(l= 4\ metros\)
Resposta Questão 7
Alternativa C.
Calculando o valor de x, temos que:
\(P = 5x+1 + 6x+2 + 2x+6 = 61\)
\(13x + 9 = 61\)
\(13x = 61 – 9\)
\(13x = 52\)
\(x = 52∶ 13 \)
\(x = 4\ cm\)
Sabendo que x = 4, então os catetos do triângulo medem:
\(5x + 1 = 4 ⋅5 + 1 = 21\)
\(2x + 6 = 2⋅4 + 6 = 8 + 6 = 14 \)
Logo, a área desse triângulo é:
\(A = \frac{21⋅14}2\)
\(A = 21 ⋅7\)
\(A=147\ cm^2\)
Resposta Questão 8
Alternativa B.
Calculando a área do terreno, que é um triângulo, temos que:
\(A=\frac{12⋅15}2\)
\(A= 6 ⋅15 \)
\(A=90\ m^2\)
Agora calculando a área do tablado:
\(A=3^2=9\ m^2\)
A área a ser gramada é a diferença entre a área do terreno e a área do tablado:
\(A_G=90-9=81\ m^2\)
Resposta Questão 9
Alternativa B
Calculando a área do retângulo:
\(A=24 ⋅8 = 192\ m^2\)
Sabendo que as áreas dos terrenos são iguais, para encontrar a altura do terreno do Thiago, temos que:
\(A=\frac{b⋅h}2\)
\(192=\frac{16⋅h}2\)
\(192 = 8h\)
\(h=\frac{192}{8}\)
\(h=24\ metros\)
Resposta Questão 10
Alternativa C.
Sabemos que a área do retângulo é igual ao produto da base pela altura e que a área do triângulo é igual à metade do produto entre a base e a altura. Sendo assim, sabemos que o triângulo tem a metade da área do retângulo, logo podemos concluir que a parte branca é a outra metade da área do retângulo, ou seja, a área branca tem a mesma medida que a área do triângulo.
\(A=\frac{30⋅36}2\)
\(A= 15 ⋅36\)
\(A=540\ m^2\)
Resposta Questão 11
Alternativa B.
Calculando a área:
\(A=\frac{b⋅h}2\)
\(24=\frac{(x+1)(x-1)}2\)
\(24⋅2=(x+1)(x-1)\)
\(48=x^2-x+x-1\)
\(48=x^2- 1\)
\(48+1=x^2\)
\(49=x^2\)
\(x=\sqrt{49}\)
\(x=7\)
Resposta Questão 12
Alternativa D.
Como sabemos o valor da hipotenusa e de um dos catetos, para encontrar o valor do outro cateto, utilizaremos o teorema de Pitágoras.
\(25^2=20^2+x^2\)
\(625=400+x^2\)
\(625-400=x^2\)
\(225=x^2\)
\(x=\sqrt{225}\)
\(x=15\)
Sabendo que o outro cateto mede 15, então calcularemos a área do triângulo retângulo:
\(A=\frac{15⋅20}2\)
\(A= 15 ⋅10 \)
\(A=150\ m^2\)
Resposta Questão 13
Alternativa B.
A área de um dos triângulos brancos possui base igual a 0,25 metro e altura igual a 0,5 metro. Como são quatro triângulos, a área clara será de:
\(A=4\cdot\frac{0,25\cdot0,5}2\)
\(A = 2 (0,25 \cdot 0,5)\)
\(A = 0,25\ m^2\)
Calculando a área escura, sabemos que a área do quadrado é:
1² = 1
\(1 – 0,25 = 0,75\ m^2\)
Logo, o preço será:
\(P = 0,25\cdot50 + 0,75\cdot30\)
\(P = 12,5 + 22,5 = 35\ reais\)



