Questão 1
(PUC) O gráfico a seguir representa a forma de uma onda com frequência constante.
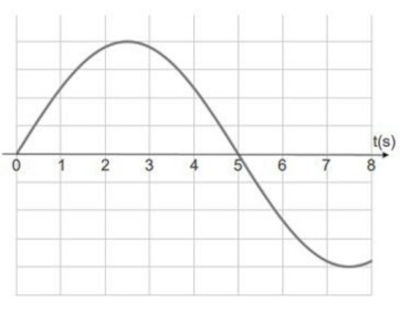
Sendo o comprimento de onda igual a 20 m, o período e a velocidade de propagação da onda valem, respectivamente, _______ e _______.
A) 10 s – 1,0 m/s
B) 10 s – 2,0 m/s
C) 20 s – 1,0 m/s
D) 20 s – 2,0 m/s
Questão 2
(Mackenzie) As antenas das emissoras de rádio emitem ondas eletromagnéticas que se propagam na atmosfera com a velocidade da luz (3,0·105 km/s) e com frequências que variam de uma estação para a outra. A rádio CBN emite uma onda de frequência 90,5 MHz e comprimento de onda aproximadamente igual a:
A) 2,8 m
B) 3,3 m
C) 4,2 m
D) 4,9 m
E) 5,2 m
Questão 3
(Urca) Uma onda eletromagnética monocromática possui comprimento de onda “L” e frequência “F”. Se “c” é a velocidade da luz no vácuo, podemos dizer que “L”, “F” e “c” estão relacionados por:
A) L = Fc
B) Lc = F
C) LF = c
D) LFc = 0
E) LF + c = 0
Questão 4
(Fuvest) Uma fonte emite ondas sonoras de 200 Hz. A uma distância de 3400 m da fonte, está instalado um aparelho que registra a chegada das ondas através do ar e as remete de volta através de um fio metálico retilíneo. O comprimento dessas ondas no fio é 17 m. Qual o tempo de ida e volta das ondas? Dado: velocidade do som no ar igual a 340 m/s.
A) 11 s
B) 17 s
C) 22 s
D) 34 s
E) 200 s
Questão 5
Determine a frequência de oscilação de uma onda eletromagnética que se desloca no vácuo com comprimento de onda de 500·10-9 m, sabendo que a velocidade da onda é igual a 3·108 m/s.
A) 4·1014 Hz
B) 5·1014 Hz
C) 6·1014 Hz
D) 7·1014 Hz
E) 8·1014 Hz
Questão 6
Qual deve ser a velocidade de propagação de uma onda de comprimento de onda de 1000 m e período 5s?
A) 0 m/s
B) 50 m/s
C) 100 m/s
D) 150 m/s
E) 200 m/s
Questão 7
Sabendo que a frequência de oscilação de certa onda é de 10 Hz e que sua velocidade de propagação é de 360 m/s, qual deve ser o seu comprimento de onda?
A) 24 m
B) 28 m
C) 32 m
D) 36 m
E) 40 m
Questão 8
Uma onda A, de comprimento de 20 m, se propaga em uma superfície com velocidade de 0,5 m/s. Com base nessas informações, calcule o seu período.
A) 10 s
B) 20 s
C) 30 s
D) 40 s
E) 50 s
Questão 9
Calcule a velocidade de propagação de uma onda de comprimento de onda 6 ·10-9 m e frequência de 3·1010 Hz.
A) 180 m/s
B) 360 m/s
C) 540 m/s
D) 720 m/s
E) 900 m/s
Questão 10
Duas ondas, A e B, se propagam com a mesma velocidade, com mas diferentes comprimentos de onda e frequência. Sabendo que o comprimento da onda A é de 100 m, que o comprimento da onda B é de 80 m e que a frequência de B é 10 + fA, determine a frequência da onda A.
A) 35 Hz
B) 40 Hz
C) 45 Hz
D) 50 Hz
E) 55 Hz
Questão 11
Sabendo que o comprimento de uma onda é de 3 m e que o seu período é 1,5 s, qual é a sua velocidade de propagação?
A) 0 m/s
B) 51 m/s
C) 2 m/s
D) 3 m/s
E) 4 m/s
Questão 12
Quais das alternativas apresentam as unidades de medidas relacionadas à velocidade da propagação de onda.
I. A velocidade da propagação de onda é medida em segundos.
II. O período é medido em segundos.
III. O comprimento de onda é medido em Hertz.
IV. A frequência é medida em Hertz.
A) Alternativas I e II.
B) Alternativas II e III.
C) Alternativas III e IV.
D) Alternativas I e IV.
E) Alternativas II e IV.
Resposta Questão 1
Alternativa B.
Com base no gráfico, podemos perceber que, em 5 s, a onda descreveu meio período de oscilação, então o seu período de oscilação é de 10 s.
Por fim, calcularemos a velocidade da propagação de onda por meio da sua fórmula:
\(v=\frac{\lambda}{T}\)
\(v=\frac{20}{10}\)
\(v=2\ m/s \)
Resposta Questão 2
Alternativa B.
Primeiramente, converteremos a velocidade da luz de km/s para m/s:
3,0·105 km/s=3,0·108 m/s
Calcularemos o comprimento de onda por meio da fórmula da velocidade da propagação de onda:
\(v=\lambda \cdot f\)
\(3,0\cdot 10^8=\lambda \cdot 90,5 M\)
Em que M significa mega, que equivale a 106
:
\(3,0\cdot 10^8=\lambda \cdot 90,5 \cdot 10^6\)
\(\lambda =\frac{3,0\cdot 10^8}{90,5\cdot 10^6} \)
\(\lambda ≅0,033\cdot 10^2 \)
\(\lambda ≅3,3\ m \)
Resposta Questão 3
Alternativa C.
A fórmula da velocidade da propagação de onda é dada pela expressão:
\(v = \lambda \cdot f\)
Em que:
-
v
→ velocidade de propagação da onda. -
λ
→ comprimento de onda. -
f
→ frequência.
Então, nessa situação, temos:
\(L \cdot F = c\)
Resposta Questão 4
Alternativa A.
Primeiramente, calcularemos o tempo de ida por meio da fórmula da velocidade linear:
\(v= \frac{d}{t_i}\)
\(340= \frac{3400}{t_i}\)
\(t_i=\frac{3400}{340}\)
\(t_i=10 s\)
Então calcularemos a velocidade do fio por meio da fórmula da velocidade da propagação de onda:
\(v = \lambda \cdot f\)
\(v = 17 \cdot 200\)
\(v = 3400\ m/s\)
Depois calcularemos o tempo de volta, novamente por meio da fórmula da velocidade linear:
\(v=\frac{d}{t_v}\)
\(3400=\frac{3400}{t_v}\)
\(t_v=\frac{3400}{3400}\)
\(t_v=1 s\)
Por fim, calcularemos o tempo total por meio da soma do tempo de ida com o tempo de volta:
\(t_t=t_i+t_v \)
\(t_t=10+1 \)
\(t_t=11 s \)
Resposta Questão 5
Alternativa C.
Calcularemos a frequência de oscilação dessa onda eletromagnética por meio da fórmula da velocidade da propagação da onda:
\(v = \lambda \cdot f\)
\(3\cdot 10^8 = 500 \cdot 10^{-9} \cdot f\)
\(f= \frac{3\cdot 10^8}{500\cdot 10^{-9}}\)
\(f= 0,006\cdot 10^{8+9}\)
\(f= 6\cdot 10^{-3} \cdot 10^{8+9}\)
\(f= 6\cdot 10^{8+9-3}\)
\(f= 6\cdot 10^{14} Hz\)
Resposta Questão 6
Alternativa E.
Calcularemos a velocidade da propagação de onda por meio da sua fórmula:
\(v=\frac{\lambda}{T}\)
\(v=\frac{1000}{5}\)
\(v=200\ m/s \)
Resposta Questão 7
Alternativa D.
Calcularemos o comprimento de onda por meio da fórmula da velocidade da propagação de onda:
\(v=\lambda \cdot f \)
\(360=\lambda \cdot 10\)
\(\lambda=\frac{360}{10}\)
\(\lambda= 36m\)
Resposta Questão 8
Alternativa D.
Calcularemos o período da por meio da fórmula da velocidade da propagação de onda:
\(v=\frac{\lambda}{T}\)
\(0,5=\frac{20}{T}\)
\(T=40 s \)
Resposta Questão 9
Alternativa A.
Calcularemos a velocidade da propagação de onda por meio da sua fórmula:
\(v = \lambda \cdot f\)
\(v =6\cdot 10^{-9} \cdot 3\cdot 10^{10}\)
\(v= 18\cdot 10^{-9+10}\)
\(v= 18\cdot 10^1\)
\(v= 180\ m/s\)
Resposta Questão 10
Alternativa B.
Calcularemos a frequência da onda A igualando sua velocidade de propagação à da onda B:
vA=vB
Substituindo pela fórmula da velocidade de propagação da onda, temos:
\(\lambda_A \cdot f_A = \lambda_B \cdot f_B\)
\(100 \cdot f_A = 80 \cdot f_B\)
Sabendo que fB=10 + fA, então:
\(100 \cdot f_A = 80 \cdot (10 + f_A)\)
\(100 \cdot f_A = 800 + 80 \cdot f_A\)
\(100 \cdot f_A - 80 \cdot f_A= 800\)
\(20 \cdot f_A = 800\)
\(f_A =\frac{800}{20}\)
\(f_A =40\ Hz\)
Resposta Questão 11
Alternativa C.
Calcularemos a velocidade da propagação de onda por meio da sua fórmula:
\(v =\frac{\lambda}{T}\)
\(v =\frac{3}{1,5}\)
\(v=2\ m/s\)
Resposta Questão 12
Alternativa E.
I. A velocidade da propagação de onda é medida em segundos. (incorreta)
A velocidade da propagação de onda é medida em metros por segundos.
II. O período é medido em segundos. (correta)
III. O comprimento de onda é medido em Hertz. (incorreta)
O comprimento de onda é medido em metros.
IV. A frequência é medida em Hertz. (correta)
