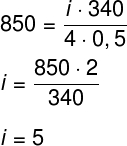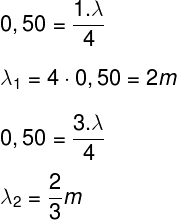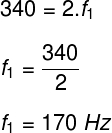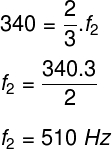Questão 1
Em um tubo sonoro fechado de comprimento igual a 0,5 m, forma-se um harmônico de frequência igual a 850 Hz. Sendo a velocidade do som no interior do tubo igual a 340 m/s, o harmônico formado nesse tubo é igual a:
a) sexto harmônico
b) primeiro harmônico
c) segundo harmônico
d) quinto harmônico
e) terceiro harmônico
Questão 2
(UFRJ-RJ) O grupo brasileiro Uakti constrói seus próprios instrumentos musicais. Um deles consiste em vários canos de PVC de comprimentos variados. Uma das pontas dos canos é mantida fechada por uma membrana que emite sons característicos ao ser percutida pelos artistas, enquanto a outra é mantida aberta. Sabendo-se que o módulo da velocidade do som no ar vale 340 m/s, é correto afirmar que as duas frequências mais baixas emitidas por um desses tubos, de comprimento igual a 50 cm, são:
a) 170 Hz e 340 Hz
b) 170 Hz e 510 Hz
c) 200 Hz e 510 Hz
d) 340 Hz e 510 Hz
e) 200 Hz e 340 Hz
Questão 3
(UFJF-MG) Considerando que a velocidade do som no ar é igual a 340 m/s e que o canal auditivo humano pode ser comparado a um tubo de órgão com uma extremidade aberta e a outra fechada, qual deveria ser o comprimento do canal auditivo para que a frequência fundamental de uma onda sonora estacionária nele produzida seja de 3400 Hz?
a) 2,5 m
b) 2,5 cm
c) 0,25 cm
d) 0,10 m
e) 0,10 cm
Questão 4
(Udesc) Dois tubos sonoros de um órgão têm o mesmo comprimento, um deles é aberto e o outro fechado. O tubo fechado emite o som fundamental de 500 Hz na temperatura de 20ºC e na pressão atmosférica. Entre as frequências a seguir, indique a que esse tubo não é capaz de emitir.
a) 1500 Hz
b) 4500 Hz
c) 1000 Hz
d) 2500 Hz
e) 3500 Hz
Resposta Questão 1
Letra E
A frequência no tubo sonoro fechado é dada por:
- i é um número ímpar e inteiro que nos informa a ordem do harmônico (i = 1,3,5,7);
- v é a velocidade do som no interior do tubo;
- L é o comprimento do tubo.
Dessa forma e de acordo com os dados fornecidos pelo enunciado do exercício, temos que:
O harmônico de índice 5 equivale ao terceiro harmônico, pois, no tubo fechado, só se admitem valores ímpares de harmônicos (1,3,5,7...).
Resposta Questão 2
Letra B
A relação entre o comprimento do tubo fechado e o comprimento da onda estacionária é determinada pela equação a seguir:
Dessa forma, os comprimentos de onda mais baixos são aqueles relacionados ao primeiro harmônico e o segundo harmônico (n = 1 e 3), portanto:
Para calcular as frequências relacionadas a esses dois comprimentos de onda, usamos a equação:
Vale dizer que v é a velocidade do som no tubo, λ é o comprimento de onda, e f é a a frequência. Dessa forma, temos para a frequência mais baixa (f1):
Da mesma forma, fazemos o cálculo para a frequência do segundo harmônico:
Portanto, os módulos das menores frequências possíveis nesses tubos sonoros são de 170 Hz e 510 Hz, respectivamente.
Resposta Questão 3
Letra B
De acordo com os dados fornecidos pelo exercício, queremos calcular o comprimento (L) de um tubo sonoro fechado que forme um harmônico fundamental (n = 1) cuja frequência equivale a 3400 Hz. A velocidade do som nesse tubo é de 340 m/s, portanto:
O canal auditivo pode ser comparado a um tubo sonoro fechado com o comprimento de 2,5 cm.
Resposta Questão 4
Letra C
A relação entre a enésima frequência produzida por um tubo sonoro e a frequência fundamental é dada por:
Vamos considerar que n = 1,3,5,7 (somente números ímpares) e f0 é a frequência fundamental, portanto, não é possível que haja nenhuma frequência que seja um múltiplo par da frequência fundamental. A frequência de 1.000 Hz não pode ser produzida por esse tubo fechado.