Questão 1
(Unifesp) Você constrói três resistências elétricas, RA, RB e RC, com fios de mesmo comprimento e com as seguintes características:
I. O fio de RA tem resistividade de 1,0⋅10−6Ω·m e diâmetro de 0,50 mm.
II. O fio de RB tem resistividade de 1,2⋅10−6Ω·m e diâmetro de 0,50 mm.
III. O fio de RC tem resistividade de 1,5⋅10−6Ω·m e diâmetro de 0,40 mm.
Pode-se afirmar que:
A) RA>RB>RC.
B) RB>RA>RC.
C) RB>RC>RA.
D) RC>RA>RB.
E) RC>RB>RA.
Questão 2
(Uefs-BA) Dois condutores metálicos, A e B, de mesmo comprimento e constituídos do mesmo material, possuem áreas de secção transversal respectivamente iguais a SA e SB e estão em equilíbrio térmico entre si. Pode-se afirmar que o condutor A apresenta, em relação ao condutor B, igual:
A) massa
B) resistividade elétrica
C) condutividade elétrica
D) resistência elétrica
E) grau de agitação dos átomos da rede cristalina
Questão 3
(UFC-CE) Um pássaro pousa em um dos fios de uma linha de transmissão de energia elétrica. O fio conduz uma corrente elétrica i=1.000 A, e sua resistência, por unidade de comprimento, é de 5,0⋅10−5 Ω/m. A distância que separa os pés do pássaro, ao longo do fio, é de 6,0 cm. A diferença de potencial, em milivolts (mV), entre os seus pés é:
A) 1,0
B) 2,0
C) 3,0
D) 4,0
E) 5,0
Questão 4
(Uneb-BA) Um resistor ôhmico, quando submetido a uma ddp de 40 V, é atravessado por uma corrente elétrica de intensidade 20 A. Quando a corrente que o atravessa for igual a 4 A, a ddp, em volts, nos seus terminais, será:
A) 8
B) 12
C) 16
D) 20
E) 30
Questão 5
Um resistor de 300 Ω é atravessado por uma corrente elétrica de 15 mA. A diferença de potencial entre os terminais do resistor é:
A) 3,5
B) 4,5
C) 5,5
D) 6,5
E) 7,5
Questão 6
Ao ligar um resistor a uma tomada de 110 V, ele é atravessado por uma corrente elétrica de 8 A. Considerando as informações dadas, qual é o valor da resistência elétrica desse resistor?
A) 13,75 Ω
B) 15,54 Ω
C) 8,23 Ω
D) 11,48 Ω
E) 13,62 Ω
Questão 7
Determine a corrente elétrica em um resistor de 25 Ω que é inserido em uma ddp de 220 V.
A) 8,8⋅10−1 A
B) 8,8⋅10−2 A
C) 8,8⋅101 A
D) 8,8⋅102 A
E) 8,8 A
Questão 8
O fio B possui resistividade elétrica igual a três vezes a resisitividade elétrica do fio A. Enquanto o fio A tem quatro vezes o comprimento do fio B, sabendo que ambos possuem a mesma área de secção transversal, determine a relação entre as resistências do fio A e do fio B:
A) RA=1,50⋅RB
B) RA=0,75⋅RB
C) RB=RA
D) RB=0,75⋅RA
E) RB=1,50⋅RA
Questão 9
Um cabo de cobre, com comprimento de 50 m e área transversal de 10−4 m, apresenta uma resistividade de 1,7⋅10−6 Ω⋅m. Determine a sua resistência elétrica.
A) 0,085 Ω
B) 0,85 Ω
C) 0,0085 Ω
D) 85 Ω
E) 8,5 Ω
Questão 10
Qual(is) (das) alternativa(s) apresenta(m) a unidade de medida correspondente à grandeza física estudada em resistência elétrica?
I. A diferença de potencial é medida em Volts.
II. A resistência elétrica é medida em Ohm por metro.
III. A corrente elétrica é medida em Ampere.
IV. A resistividade do material é medida em metros.
V. O comprimento do condutor é medido em metros quadrados.
VI. A área transversal do condutor é medida em metros quadrados.
A) Alternativas I, II e III.
B) Alternativas IV, V e VI.
C) Alternativas I, III e VI.
D) Todas as alternativas estão corretas.
E) Nenhuma das alternativas está correta.
Questão 11
Qual alternativa abaixo corresponde à principal função da resistência elétrica em um circuito elétrico?
A) Armazenar cargas elétricas.
B) Gerar energia elétrica.
C) Converter energia elétrica em energia cinética.
D) Armazenar energia elétrica.
E) Conter a passagem da corrente elétrica.
Questão 12
Existem diversos fatores que influenciam na capacidade da resistência elétrica de realizar sua função. Qual dos fatores descritos abaixo NÃO influencia na resistência elétrica?
A) Comprimento do condutor.
B) Área de secção transversal.
C) Temperatura.
D) Pressão.
E) Resistividade do material.
Resposta Questão 1
Alternativa D
Por meio da fórmula da segunda lei de Ohm, calcularemos os valores das resistências elétricas:
R=ρ⋅LA
A área é calculada por π⋅r2:
R=ρ⋅Lπ⋅r2
O raio é metade do diâmetro:
R=ρ⋅Lπ⋅(d/2) 2
Encontrando o valor da resistência RA:
RA=ρA⋅Lπ⋅(d/2) 2
Convertendo o diâmetro de milímetro para metros, 0,50 mm = 0,0005 m, e considerando π = 3,14:
RA=1,0·10−6⋅L3,14⋅(0,0005/2)2
RA=1,0·10−6⋅L3,14⋅6,25⋅10−8
RA=1,0·10−6⋅L1,9625⋅10−7
RA≈0,509·10−6+7 L
RA≈0,509·101 L
RA≈5,09 L
Encontrando o valor da resistência RB:
RB=ρB⋅Lπ⋅(d/2) 2
Convertendo o diâmetro de milímetro para metros, 0,80 mm = 0,0008 m, e considerando π = 3,14:
RB=1,2·10−6⋅L3,14⋅(0,0008/2)2
RB=1,2·10−6⋅L3,14⋅1,6⋅10−7
RB=1,2·10−6⋅L5,024⋅10−7
RB≈0,238·10−6+7 L
RB≈0,238·101 L
RB≈2,38 L
Encontrando o valor da resistência RC:
RC=ρC⋅Lπ⋅(d/2) 2
Convertendo o diâmetro de milímetro para metros, 0,40 mm = 0,0004 m, e considerando π = 3,14:
RC=1,5·10−6⋅L3,14⋅(0,0004/2)2
RC=1,5·10−6⋅L3,14⋅4⋅10−8
RC=1,5·10−6⋅L1,256⋅10−7
RC≈1,194·10−6+7 L
RC≈1,194·101 L
RC≈11,94 L
Então, RC>RA>RB.
Resposta Questão 2
Alternativa B
Como os dois condutores são constituídos do mesmo material, ambos possuem a mesma resistividade elétrica.
Resposta Questão 3
Alternativa C
Primeiramente, encontraremos o valor da resistência elétrica na distância que separa os pés do pássaro. Já que a resistência foi dada em função do comprimento do fio, basta multiplicarmos seu valor pelo comprimento:
R=Rpor comprimento⋅L
Convertendo a distância entre os pés do pássaro de centímetro para metros, 6 cm = 0,06 m, então:
R=5,0⋅10−5⋅0,06
R=0,3⋅10−5 Ω
Por fim, para calcularmos a tensão elétrica, basta utilizarmos a primeira lei de Ohm:
U=R⋅i
U=0,3⋅10−5⋅1000
U=300⋅10−5
U=3⋅102⋅10−5
U=3⋅102−5
U=3⋅10−3 V
U=3 mV
Resposta Questão 4
Alternativa A
Primeiramente, calcularemos o valor do resistor quando atravessado pela corrente de 20 A e sujeito à ddp de 40 V, por meio da fórmula da primeira lei de Ohm:
U=R⋅i
40=R⋅20
40 20=R
2Ω=R
Por fim, encontraremos a ddp nos terminais quando o resistor é atravessado pela corrente de 4 A:
U=R⋅i
U=2⋅4
U=8 V
Resposta Questão 5
Alternativa B
Encontraremos o valor da tensão por meio da primeira lei de Ohm:
U=R⋅i
U=300⋅15m
O m de 15 mA é mili, cujo valor é 10−3:
U=300⋅15⋅10−3
U=4500⋅10−3
U=4,5⋅103⋅10−3
U=4,5⋅103−3
U=4,5⋅101
U=4,5 V
Resposta Questão 6
Alternativa A
Encontraremos o valor da resistência por meio da primeira lei de Ohm:
R=Ui
R=1108
R=13,75 Ω
Resposta Questão 7
Alternativa E
Encontraremos o valor da corrente elétrica por meio da primeira lei de Ohm:
U=R⋅i
220=25⋅i
i=22025
i=8,8 A
Resposta Questão 8
Alternativa D
De acordo com o enunciado, temos que ρB=3⋅ρA e LA=4⋅LB. Deixaremos tudo em função do fio B, então:
LA=4⋅LB
LB=LA4
E:
ρB=3⋅ρA
Utilizando a fórmula da segunda lei de Ohm, isolaremos a área de secção transversal:
R=ρ⋅LA
A=ρ⋅LR
Como a área de secção trasnversal do fio A é igual à do fio B, faremos uma igualdade entre o fio A e o fio B:
AA=AB
ρA⋅LARA=ρB⋅LBRB
ρA⋅LARA=3⋅ρA⋅LA4RB
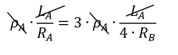
1RA=34⋅RB
4⋅RB=3⋅RA
RB=3⋅RA4
RB=0,75⋅RA
Resposta Questão 9
Alternativa B
Encontraremos o valor da resistência elétrica por meio da segunda lei de Ohm:
R=ρ⋅LA
R=1,7⋅10−6⋅5010−4
R=1,7⋅10−6⋅50⋅104
R=85⋅10−6⋅104
R=8,5⋅101⋅10−6⋅104
R=8,5⋅101−6+4
R=8,5⋅10−1
R=0,85 Ω
Resposta Questão 10
Alternativa C
I. Verdadeira
A diferença de potencial, de fato, é medida em Volts.
II. Falsa
A resistência elétrica é medida apenas em Ohm.
III. Verdadeira
A corrente elétrica é, de fato, medida em Ampere.
IV. Falsa
A resistividade do material é medida em Ohm por metro.
V. Falsa
O comprimento do condutor é medido em metros.
VI. Verdadeira
A área transversal do condutor é, de fato, medida em metros quadrados.
Resposta Questão 11
Alternativa E
A principal função da resistência elétrica é de conter a passagem da corrente elétrica para o restante do circuito elétrico.
Resposta Questão 12
Alternativa D
O comprimento do condutor e a resistividade do material são proporcionais à resistência elétrica, enquanto a área de secção transversal é inversamente proporcional à resistência. A temperatura está intimamente ligada à resistividade do material, influenciando indiretamente a resistência. Portanto, o único fator que não a influencia é a pressão.



