Questão 1
(UFRGS) Um pêndulo simples, de comprimento L, tem um período de oscilação T, num determinado local. Para que o período de oscilação passe a valer 2T, no mesmo local, o comprimento do pêndulo deve ser aumentado em:
A) 1 L.
B) 2 L.
C) 3 L.
D) 5 L.
E) 7 L.
Questão 2
(UFU) Em um laboratório de Física, um grupo de alunos, Grupo A, obtém dados, apresentados na tabela a seguir, para a frequência (em hertz) num experimento de Pêndulo Simples, utilizando-se três pêndulos diferentes.
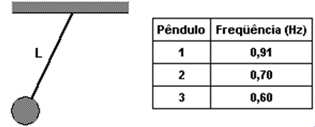
Esses resultados foram passados para um segundo grupo, Grupo B, que não compareceu à aula. Uma vez que os alunos do Grupo B não viram o experimento, os integrantes desse grupo formularam uma série de hipóteses para interpretar os resultados. Assinale a ÚNICA hipótese correta.
A) A massa do pêndulo 1 é menor do que a massa do pêndulo 2, que, por sua vez, é menor do que a massa do pêndulo 3.
B) A massa do pêndulo 1 é maior do que a massa do pêndulo 2, que, por sua vez, é maior do que a massa do pêndulo 3.
C) O comprimento L do fio do pêndulo 1 é maior do que o comprimento do pêndulo 2, que, por sua vez, é maior do que o comprimento do pêndulo 3.
D) O comprimento L do fio do pêndulo 1 é menor do que o comprimento do pêndulo 2, que, por sua vez, é menor do que o comprimento do pêndulo 3.
Questão 3
(PUC) Um pêndulo simples oscila, num local onde a aceleração da gravidade é 10 m/s², com um período de oscilação igual a 2 segundos. O comprimento desse pêndulo é:
A) 1,6 m
B) 0,16 m
C) 62,5 m
D) 6,25 m
E) 0,625 m
Questão 4
(Unifesp - Adaptada) Um estudante faz o estudo experimental de um movimento harmônico simples (MHS) com um cronômetro e um pêndulo simples como o da figura, adotando o referencial nela representado.
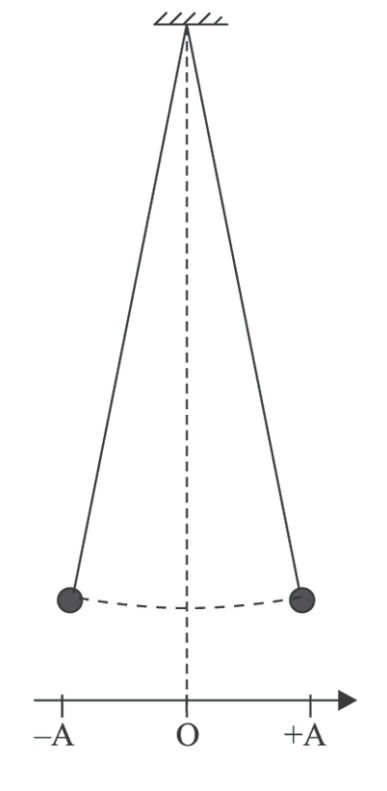
Ele desloca o pêndulo para a posição +A e o abandona quando cronometra o instante t = 0. Na vigésima passagem do pêndulo por essa posição, o cronômetro marca t = 30 s. Determine o período (T) e a frequência (f) do movimento desse pêndulo.
Questão 5
Um pêndulo simples é preso por um fio de comprimento l e oscila na Terra com um período de 3 s. A partir dessas informações calcule o comprimento do fio desse pêndulo. Considere π = 3 e aceleração da gravidade terrestre =10 m/s2 .
A) 1 m
B) 1,5 m
C) 2 m
D) 2,5 m
E) 3 m
Questão 6
Assinale as proposições corretas a respeito dos pêndulos simples.
I. A frequência de oscilação de um pêndulo simples é inversamente proporcional à aceleração da gravidade do planeta em que ele está inserido.
II. O período de oscilação de um pêndulo simples é diretamente proporcional ao comprimento do seu fio.
III. A massa do fio não interfere no período de oscilação de um pêndulo simples.
As afirmações verdadeiras são:
A) I
B) II
C) III
D) I e II
E) II e III
Questão 7
Um pêndulo simples é preso por um fio de 2 metros de comprimento e oscila em um planeta com uma frequência igual a 0,5 Hz. A partir dessas informações calcule a aceleração da gravidade do planeta em que esse pêndulo simples está. Considere π = 3.
A) 3 m/s2
B) 6 m/s2
C) 9 m/s2
D) 18 m/s2
E) 24 m/s2
Questão 8
O que acontecerá com o período de oscilação de um relógio de pêndulo que teve o comprimento do seu fio aumentado?
A) Diminuirá.
B) Aumentará.
C) Será nulo.
D) Diminuirá pela metade.
E) Aumentará o dobro.
Questão 9
Qual é o período de oscilação aproximado de um pêndulo simples preso a um fio de comprimento de 3 m que oscila na Terra?
Dados: π=3, aceleração da gravidade terrestre =10 m/s2 .
A) 3,28 s
B) 4,92 s
C) 6,56 s
D) 8,20 s
E) 9,84 s
Questão 10
Inicialmente, um pêndulo de comprimento L é posicionado em uma região com aceleração da gravidade g. Qual o novo período desse pêndulo quando quadruplicamos o seu comprimento?
A) T'=T/2
B) T'=T/4
C) T'=2∙T
D) T'=3∙T
E) T'=4∙T
Questão 11
Determine a frequência de oscilação de um pêndulo simples, sabendo que o comprimento do seu fio é de 4,5 m e que ele está localizado em um planeta com aceleração da gravidade de 1,62 m/s2. Considere π = 3.
A) 0,5 Hz
B) 0,4 Hz
C) 0,3 Hz
D) 0,2 Hz
E) 0,1 Hz
Questão 12
Qual(is) das alternativa(s) apresenta(m) a unidade de medida correspondente às grandezas físicas estudadas em pêndulo simples?
I. A frequência é medida em Hertz.
II. O período é medido em segundo.
III. O comprimento do fio é medido em metros por segundo.
IV. A aceleração da gravidade é medida em metros.
Está(ão) correta(s):
A) I, II.
B) III, IV.
C) I, IV.
D) II, III.
E) I, II e IV.
Resposta Questão 1
Alternativa C.
O período de oscilação inicial do pêndulo simples é dado pela expressão:
\(T=2\cdot\pi\cdot\sqrt{\frac{l}{g}}\)
\(T=2\cdot\pi\cdot\frac{\sqrt l}{\sqrt g}\)
Isolando \(\sqrt l\):
\(\sqrt l=\frac{T\cdot\sqrt g}{2\cdot\pi}\)
\(2\cdot\sqrt l=\frac{T\cdot\sqrt g}{\pi}\)
Já o período de oscilação novo do pêndulo simples é dado pela expressão:
\(T\prime=2\cdot\pi\cdot\sqrt{\frac{l\prime}{g}}\)
\(T\prime=2\cdot\pi\cdot\frac{\sqrt{l\prime}}{\sqrt g}\)
\(2\ T=2\cdot\pi\cdot\frac{\sqrt{l\prime}}{\sqrt g}\)
Isolando \(\sqrt{l\prime}\):
\(\sqrt{l\prime}=\frac{2\cdot T\cdot\sqrt g}{2\cdot\pi}\)
\(\sqrt{l\prime}=\frac{T\cdot\sqrt g}{\pi}\)
\(\sqrt{l\prime}=2\cdot\sqrt l\)
\(\left(\sqrt{l\prime}\right)^2=\left(2\cdot\sqrt l\right)^2\)
\(l\prime=4\cdot l\)
O comprimento final deve ser quatro vezes o comprimento incial; como a pergunta se refere a quanto se deve aumentar, basta subtrair o comprimento final e o comprimento incial:
\(l^\prime-l=4l-1l=3l\)
Resposta Questão 2
Alternativa D.
A frequência de oscilação de um pêndulo simples é inversamente proporcional ao comprimento do seu fio, então o comprimento L do fio do pêndulo 1 é menor do que o comprimento do pêndulo 2, que, por sua vez, é menor do que o comprimento do pêndulo 3.
Resposta Questão 3
Alternativa E.
Calcularemos o comprimento do fio desse pêndulo através da fórmula do período de oscilação de um pêndulo simples:
\(T=2\cdot\pi\cdot\sqrt{\frac{l}{g}}\)
\(\frac{\pi}{2}=2\cdot\pi\cdot\sqrt{\frac{l}{10}}\)
\(\frac{\pi}{2}\cdot\frac{1}{2\cdot\pi}=\sqrt{\frac{l}{10}}\)
\(\frac{1}{4}=\sqrt{\frac{l}{10}}\)
Elevando ambos os membros ao quadrado:
\(\left(\frac{1}{4}\right)^2=\left(\sqrt{\frac{l}{10}}\right)^2\)
\(\frac{1}{16}=\frac{l}{10}\)
\(l=\frac{1}{16}\cdot10\)
\(l=0,625\ m\)
Resposta Questão 4
Alternativa C.
Primeiramente, calcularemos o período de oscilação do pêndulo para 1 oscilação completa através de uma regra de três simples:
\(30 \ segundos\ — 20\ oscilações\)
\(T — 1 \ oscilação\)
\(T\ =\frac{30}{20}\)
\(T\ =\ 1,5\ segundo\)
Por fim, calcularemos a frequência de oscilação do pêndulo através do inverso do período:
\(f\ =\ 1/T\)
\(f\ =\ 1/1,5\)
\(f\ =\ 0,67\ Hertz\)
Resposta Questão 5
Alternativa D.
Calcularemos o comprimento do fio desse pêndulo através da fórmula do período de oscilação de um pêndulo simples:
\(T=2\cdot\pi\cdot\sqrt{\frac{l}{g}}\)
\(3=2\cdot3\cdot\sqrt{\frac{l}{10}}\)
\(3=6\cdot\sqrt{\frac{l}{10}}\)
\(\frac{3}{6}=\sqrt{\frac{l}{10}}\)
\(\frac{1}{2}=\sqrt{\frac{l}{10}}\)
\(\left(\frac{1}{2}\right)^2=\left(\sqrt{\frac{l}{10}}\right)^2\)
\(\frac{1}{4}=\frac{l}{10}\)
\(l=\frac{1}{4}\cdot10\)
\(l=2,5\ m\)
Resposta Questão 6
Alternativa E.
I. A frequência de oscilação de um pêndulo simples é inversamente proporcional à aceleração da gravidade do planeta em que ele está inserido. (incorreta)
A frequência de oscilação de um pêndulo simples é diretamente proporcional à aceleração da gravidade do planeta em que ele está inserido.
II. O período de oscilação de um pêndulo simples é diretamente proporcional ao comprimento do seu fio. (correta)
III. A massa do fio não interfere no período de oscilação de um pêndulo simples. (correta)
Resposta Questão 7
Alternativa D.
Calcularemos a aceleração da gravidade em que esse pêndulo está inserido através da fórmula da frequência de oscilação de um pêndulo simples:
\(f=\frac{1}{2\cdot\pi}\cdot\sqrt{\frac{g}{l}}\)
\(0,5=\frac{1}{2\cdot3}\cdot\sqrt{\frac{g}{2}}\)
\(0,5=\frac{1}{6}\cdot\sqrt{\frac{g}{2}}\)
\(\frac{0,5\cdot6}{1}=\sqrt{\frac{g}{2}}\)
\(3=\sqrt{\frac{g}{2}}\)
\(3^2=\left(\sqrt{\frac{g}{2}}\right)^2\)
\(9=\frac{g}{2}\)
\(g=18\ m/s^2\)
Resposta Questão 8
Alternativa B.
Quando aumentamos o comprimento do fio de um pêndulo, a distância que ele percorrer será maior e ele levará mais tempo em cada oscilação, portanto o seu período aumentará.
Resposta Questão 9
Alternativa A.
Calcularemos o período de oscilação do pêndulo simples através da sua fórmula:
\(T=2\cdot\pi\cdot\sqrt{\frac{l}{g}}\)
\(T=2\cdot3\cdot\sqrt{\frac{3}{10}}\)
\(T=2\cdot3\cdot\sqrt{0,3}\)
\(T=2\cdot3\cdot0,55\)
\(T\cong3,28\ s\)
Resposta Questão 10
Alternativa C.
O período inicial do pêndulo é dado pela expressão:
\(T=2\cdot\pi\cdot\sqrt{\frac{l}{g}}\)
Já o novo período do pêndulo pode ser dado pela expressão:
\(T\prime=2\cdot\pi\cdot\sqrt{\frac{4l}{g}}\)
Retirando o termo 4 da raíz é possível compararmos o período novo ao período inicial:
\(T\prime=2\cdot2\cdot\pi\sqrt{\frac{l}{g}}\)
\(T\prime=2\cdot T\)
Resposta Questão 11
Alternativa E.
Calcularemos a frequência de oscilação desse pêndulo através da sua fórmula:
\(f=\frac{1}{2\cdot\pi}\cdot\sqrt{\frac{g}{l}}\)
\(f=\frac{1}{6}\cdot\sqrt{\frac{1,62}{4,5}}\)
\(f=\frac{1}{6}\cdot\sqrt{0,36}\)
\(f=\frac{1}{6}\cdot0,6\)
\(f=0,1\ Hz\)
Resposta Questão 12
Alternativa A.
I. A frequência é medida em Hertz. (correta)
II. O período é medido em segundo. (correta)
III. O comprimento do fio é medido em metros por segundo. (incorreta)
O comprimento do fio é medido em metros.
IV. A aceleração da gravidade é medida em metros. (incorreta)
A aceleração da gravidade é medida em metros por segundo ao quadrado.
