Questão 1
(IFBA) O Beach park, localizado em Fortaleza – CE é o maior parque aquático da América Latina situado na beira do mar. Uma das suas principais atrações é um toboágua chamado “Insano”. Descendo esse toboágua, uma pessoa atinge sua parte mais baixa com velocidade módulo 28 m/s. Considerando-se a aceleração da gravidade com módulo g = 10 m/s2 e desprezando-se os atritos, estima-se que a altura do toboágua, em metros, é de:
A) 28
B) 274,4
C) 40
D) 2,86
E) 32
Questão 2
(Uern) Seja o gráfico da velocidade em função do tempo de um corpo em movimento retilíneo uniformemente variado representado abaixo.
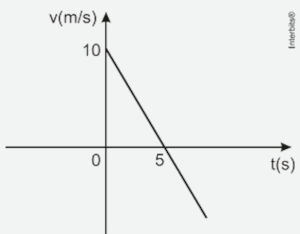
Considerando a posição inicial desse movimento igual a 46 m, então a posição do corpo no instante t = 8 s é
A) 54 m.
B) 62 m.
C) 66 m.
D) 74 m.
Questão 3
(PUC) Um carro parte do repouso com aceleração de 5,0 m/s2 e percorre uma distância de 1,0 km. Qual é o valor da velocidade média do carro, em m/s, nesse trecho?
A) 2,5
B) 20
C) 50
D) 100
E) 200
Questão 4
(UFRGS) Um atleta, partindo do repouso, percorre 100 m em uma pista horizontal retilínea, em 10 s, e mantém a aceleração constante durante todo o percurso. Desprezando a resistência do ar, considere as afirmações abaixo sobre esse movimento.
I - O módulo de sua velocidade média é 36 km/h.
II - O módulo de sua aceleração é 10 m/s2.
III - O módulo de sua maior velocidade instantânea é 10 m/s.
Quais estão corretas?
A) Apenas I.
B) Apenas II.
C) Apenas III.
D) Apenas I e II.
E) I, II e III.
Questão 5
Em uma competição de corrida, uma pessoa chega à linha de chegada com velocidade de 8 m/s. Sabendo que a sua aceleração foi de 0,5 m/s2, qual deve ser o tamanho do percuso da corrida?
A) 16 m
B) 32 m
C) 48 m
D) 64 m
E) 80 m
Questão 6
Determine o tempo que uma pessoa demorou para partir do repouso e atingir uma velocidade de 4 m/s, considerando que a sua aceleração era de 0,2 m/s2.
A) 2 s
B) 5 s
C) 10 s
D) 15 s
E) 20 s
Questão 7
Um automóvel se move em uma avenida com velocidade de 360 m/s durante 50 segundos, então a aceleração média desse automóvel será de:
A) 4,8 m/s2.
B) 5,6 m/s2.
C) 6,4 m/s2.
D) 7,2 m/s2.
E) 8,0 m/s2.
Questão 8
Em uma situação hipotética, um automóvel atingiu uma velocidade final de 80 m/s após 10 segundos, com uma aceleração de 6 m/s2. A partir dessas informações, calcule a sua velocidade inicial.
A) 20 m/s
B) 40 m/s
C) 60 m/s
D) 80 m/s
E) 100 m/s
Questão 9
Um móvel parte do repouso em movimento uniformemente variado e, após percorrer uma distância x, atinge uma velocidade de 12 m/s com aceleração de 1,2 m/s2. Tendo isso em vista, o percurso foi de:
A) 20 m.
B) 30 m.
C) 40 m.
D) 50 m.
E) 60 m.
Questão 10
Quanto tempo demora para que uma moto se desloque 5000 metros, considerando que a sua aceleração era de 0,2 m/s2 e que ela partiu do repouso.
Considere \(\sqrt 5 = 2,24\).
A) 145,3 s
B) 223,6 s
C) 364,1 s
D) 472,8 s
E) 596,4 s
Questão 11
Sabendo que uma pessoa, partindo do repouso, percorreu 360 m com uma aceleração de 0,05 m/s2, calcule qual foi a sua velocidade final.
A) 4 m/s
B) 5 m/s
C) 6 m/s
D) 7 m/s
E) 8 m/s
Questão 12
Quais das alternativas apresentam as unidades de medida correspondentes às grandezas físicas estudadas no movimento uniformemente variado?
I - A aceleração é medida em metros por segundo ao quadrado.
II - A velocidade é medida em metros por segundo.
III - O deslocamento é medido em metros quadrados.
IV - O tempo é medido em segundos ao quadrado.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e III.
D) Alternativas II e IV.
E) Alternativas I e IV.
Resposta Questão 1
Alternativa C.
Calcularemos a altura do toboágua empregando a equação de Torricelli:
\(v_f^2 = v_i^2 + 2 \cdot a \cdot \Delta x \\ 28^2 = 0^2 + 2 \cdot 10 \cdot \Delta x \\ 784 = 0 + 20 \cdot \Delta x \\ 784 = 20 \cdot \Delta x \\ \Delta x = \frac{784}{20} \\ \Delta x = 39{,}2 \, \text{m} \\ \Delta x \cong 40 \, \text{m} \)
Resposta Questão 2
Alternativa B.
Primeiramente calcularemos a aceleração média empregando a fórmula:
\(a_m = \frac{\Delta v}{\Delta t} \\ a_m = \frac{v_f - v_i}{t_f - t_i} \\ a_m = \frac{0 - 10}{5 - 0} \\ a_m = \frac{-10}{5} \\ a_m = -2 \, \text{m/s}^2\)
Por fim, calcularemos a posição final no tempo de 8 segundos empregando a fórmula da função horária da posição no movimento uniformemente variado (MUV):
\(x_f = x_i + v_i \cdot t + \frac{a \cdot t^2}{2} \\ x_f = 46 + 10 \cdot 8 + \frac{(-2) \cdot 8^2}{2} \\ x_f = 46 + 80 - 64 \\ x_f = 62 \, \text{m}\)
Resposta Questão 3
Alternativa C.
Primeiramente, transformaremos a variação da distância de quilômetro para metro:
1 km = 1000 m
Depois, calcularemos o tempo empregando a fórmula da função horária da posição no movimento uniformemente variado (MUV):
\(x_f = x_i + v_i \cdot t + \frac{a \cdot t^2}{2} \\ x_f - x_i = v_i \cdot t + \frac{a \cdot t^2}{2} \\ \Delta x = v_i \cdot t + \frac{a \cdot t^2}{2} \\ 1000 = 0 \cdot t + \frac{5 \cdot t^2}{2} \\ 1000 = \frac{5 \cdot t^2}{2} \\ t^2 = \frac{1000 \cdot 2}{5} \\ t^2 = 400 \\ t = \sqrt{400} \\ t = 20 \, \text{s} \)
Por fim, calcularemos a velocidade média:
\(v_m = \frac{\Delta x}{\Delta t} \\ v_m = \frac{1000}{20} \\ v_m = 50 \, \text{m/s} \)
Resposta Questão 4
Alternativa A.
- Correta. O módulo de sua velocidade média é 36 km/h.
Calcularemos a velocidade média:
\(v_m = \frac{\Delta x}{\Delta t} \\ v_m = \frac{100}{10} \\ v_m = 10 \, \text{m/s} \\ v_m = 10 \, \text{m/s} \cdot 3{,}6 \\ v_m = 36 \, \text{km/h} \)
- Incorreta. O módulo de sua aceleração é 10 m/s2.
Calcularemos a aceleração empregando a fórmula da função horária da posição no movimento uniformemente variado (MUV):
\(x_f = x_i + v_i \cdot t + \frac{a \cdot t^2}{2} \\ x_f - x_i = v_i \cdot t + \frac{a \cdot t^2}{2} \\ \Delta x = v_i \cdot t + \frac{a \cdot t^2}{2} \\ 100 = 0 \cdot 10 + \frac{a \cdot 10^2}{2} \\ 100 = 0 + \frac{a \cdot 100}{2} \\ 100 = a \cdot 50 \\ a = \frac{100}{50} \\ a = 2 \, \text{m/s}^2 \)
- Incorreta. O módulo de sua maior velocidade instantânea é 10 m/s.
Calcularemos a velocidade empregando a fórmula da função horária da velocidade no movimento uniformemente variado (MUV):
\(v_f = v_i + a \cdot t \\ v_f = 0 + 2 \cdot 10 \\ v_f = 0 + 20 \\ v_f = 20 \, \text{m/s} \)
Resposta Questão 5
Alternativa D.
Calcularemos o tamanho do percurso empregando a equação de Torricelli:
\(v_f^2 = v_i^2 + 2 \cdot a \cdot \Delta x \\ 8^2 = 0^2 + 2 \cdot 0{,}5 \cdot \Delta x \\ 64 = 0 + 1 \cdot \Delta x \\ 64 = 1 \cdot \Delta x \\ \Delta x = 64 \, \text{m} \)
Resposta Questão 6
Alternativa E.
Calcularemos o tempo empregando a fórmula da função horária da velocidade no movimento uniformemente variado (MUV):
\(v_f = v_i + a \cdot t \\ 4 = 0 + 0{,}2 \cdot t \\ 4 = 0{,}2 \cdot t \\ t = \frac{4}{0{,}2} \\ t = 20 \, \text{s} \)
Resposta Questão 7
Alternativa D.
Calcularemos a aceleração média empregando a sua fórmula:
\(a_m = \frac{\Delta v}{\Delta t} \\ a_m = \frac{360}{50} \\ a_m = 7{,}2 \, \text{m/s}^2 \)
Resposta Questão 8
Alternativa A.
Calcularemos a velocidade inicial por meio da função horária da velocidade no movimento uniformemente variado (MUV):
\(v_f = v_i + a \cdot t \\ 80 = v_i + 6 \cdot 10 \\ 80 = v_i + 60 \\ 80 - 60 = v_i \\ v_i = 20 \, \text{m/s} \)
Resposta Questão 9
Alternativa E.
Calcularemos a variação do deslocamento empregando a equação de Torricelli:
\(v_f^2 = v_i^2 + 2 \cdot a \cdot \Delta x \\ 12^2 = 0^2 + 2 \cdot 1{,}2 \cdot \Delta x \\ 144 = 0 + 2{,}4 \cdot \Delta x \\ \Delta x = \frac{144}{2{,}4} \\ \Delta x = 60 \, \text{m} \)
Resposta Questão 10
Alternativa B.
Calcularemos o tempo empregando a fórmula da função horária da posição no movimento uniformemente variado (MUV):
\(x_f = x_i + v_i \cdot t + \frac{a \cdot t^2}{2} \\ x_f - x_i = v_i \cdot t + \frac{a \cdot t^2}{2} \\ \Delta x = v_i \cdot t + \frac{a \cdot t^2}{2} \\ 5000 = 0 \cdot t + \frac{0{,}2 \cdot t^2}{2} \\ 5000 = 0 + 0{,}1 \cdot t^2 \\ 5000 = 0{,}1 \cdot t^2 \\ t^2 = \frac{5000}{0{,}1} \\ t^2 = 50000 \\ t = \sqrt{50000} \\ t \cong 223{,}6 \, \text{s} \)
Resposta Questão 11
Alternativa C.
Calcularemos a velocidade final empregando a equação de Torricelli:
\(v_f^2 = v_i^2 + 2 \cdot a \cdot \Delta x \\ v_f^2 = 0^2 + 2 \cdot 0{,}05 \cdot 360 \\ v_f^2 = 36 \\ v_f = \sqrt{36} \\ v_f = 6 \, \text{m/s}\)
Resposta Questão 12
Alternativa A.
I - A aceleração é medida em metros por segundo ao quadrado. (correta)
II - A velocidade é medida em metros por segundo. (correta)
III - O deslocamento é medido em metros quadrados. (incorreta)
O deslocamento é medido em metros.
IV - O tempo é medido em segundos ao quadrado. (incorreta)
O tempo é medido em segundos.



