Questão 1
(UEL) Um corpo de massa m é submetido a uma força resultante de módulo F, adquirindo aceleração a. A força resultante que se deve aplicar a um corpo de massa m/2 para que ele adquira aceleração 4a deve ter módulo:
A) F/2
B) F
C) 2F
D) 4F
E) 8F
Questão 2
(Enem) Em um experimento, um professor levou para a sala de aula um saco de arroz, um pedaço de madeira triangular e uma barra de ferro cilíndrica e homogênea. Ele propôs que fizessem a medição da massa da barra utilizando esses objetos. Para isso, os alunos fizeram marcações na barra, dividindo-a em oito partes iguais, e em seguida apoiaram-na sobre a base triangular, com o saco de arroz pendurado em uma de suas extremidades, até atingir a situação de equilíbrio.
Nessa situação, qual foi a massa da barra obtida pelos alunos?
A) 3.00 kg
B) 3,75 kg
C) 5.00 kg
D) 6.00 kg
E) 15.00 kg
Questão 3
(UFSM) A figura representa uma tubulação horizontal em que escoa um fluido ideal.
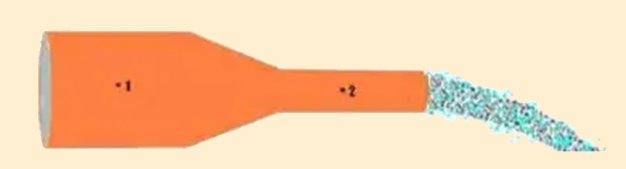
A velocidade de escoamento do fluido no ponto 1, em relação à velocidade verificada no ponto 2, e a pressão no ponto 1, em relação à pressão no ponto 2, são:
A) maior, maior
B) maior, menor
C) menor, maior
D) menor, maior
E) menor, menor
Questão 4
(CFT) Em 2005, Ano Mundial da Física, comemora-se o centenário da Teoria da Relatividade de Albert Einstein. Entre outras consequências, essa teoria poria fim à ideia do éter, meio material necessário, semelhantemente ao som, através do qual a luz se propagava. O jargão popular “tudo é relativo” certamente não se deve a ele, pois seus postulados estão fundamentados em algo absoluto: a velocidade da luz no vácuo – 300.000 km/s.
Hoje se sabe que:
I. O som propaga-se no vácuo.
II. A luz propaga-se no vácuo.
III. A velocidade da luz no vácuo é a velocidade limite do universo.
É (são) verdadeira(s):
A) todas.
B) nenhuma.
C) somente II.
D) II e III.
E) somente III.
Questão 5
Um móvel se desloca com velocidade de 60 m/s durante 5 minutos. Com base nessas informações, qual era a aceleração desse móvel?
A) 0,2 m/s2
B) 0,3 m/s2
C) 0,4 m/s2
D) 0,5 m/s2
E) 0,6 m/s2
Questão 6
Uma força F1 de 2.000N é aplicada sobre uma área A1 de 4 m2 resultando em uma pressão p1. Depois é aplicada uma força F2 de 10.000 N sobre uma área A2
. Sabendo disso, calcule a área A2, sabendo que a pressão p1 é igual a p2
.
A) 5 m2
B) 10 m2
C) 20 m2
D) 30 m2
E) 40 m2
Questão 7
Qual a força aplicada para que um corpo de 100 kg acelere a 5 m/s2?
A) 100 N
B) 200 N
C) 300 N
D) 400 N
E) 500 N
Questão 8
Determine a posição do centro de massa de um sistema de partículas de 0,01 kg posicionadas nos pontos P1 = (0,2); P2 = (-3,1); P3 = (4,0).
A) (0;0)
B) (1⁄3,1)
C) (1,1)
D) (1,1⁄3)
E) (2;2)
Questão 9
Encontre a área da seção de escoamento no ponto 1 de um tubo, sabendo que ele possui no ponto 2 uma área da seção de escoamento de 2m2 e que a velocidade de escoamento no ponto 1 é de 4 m/s e no ponto 2 é de 10 m/s .
A) 5 m2
B) 6 m2
C) 7 m2
D) 8 m2
E) 9 m2
Questão 10
Após os seus estudos a respeito da teoria da relatividade, analise qual das alternativas abaixo corresponde ao se que estuda nela.
I. Teoria da relatividade restrita.
II. Teoria da relatividade geral.
III. Dilatação do tempo.
IV. Princípio da simultaneidade.
Estão corretas:
A) I e II.
B) III e IV.
C) I e III.
D) II e IV.
E) Todas estão corretas.
Questão 11
Uma roda gigante se deslocou da posição 2 rad para 10 rad durante 2 segundos, então a sua velocidade angular média foi de:
A) 2 rad/s
B) 4 rad/s
C) 6 rad/s
D) 8 rad/s
E) 10 rad/s
Questão 12
Um mergulhador está a uma profundidade de 2 metros na água. Sabendo disso, qual é a pressão sobre ele?
Dados:
Densidade da água ρ = 1000 kg/m3
Aceleração da gravidade g = 10 m/s2
A) 0,2 ∙ 104 Pa
B) 0,5 ∙ 104 Pa
C) 1,0 ∙ 104 Pa
D) 1,5 ∙ 104 Pa
E) 2,0 ∙ 104 Pa
Resposta Questão 1
Alternativa C.
Primeiramente, calcularemos a força resultante antes, por meio da fórmula da segunda lei de Newton:
\(F=m \cdot a\)
Depois calcularemos a força resultante nova, quando mudamos a massa e a aceleração, por meio da fórmula da segunda lei de Newton:
\(F'=m' \cdot a'\)
\(F' = \frac{m}{2} \cdot 4a\)
\(F' = \frac{4 \cdot m \cdot a}{2}\)
\(F'=2 \cdot m \cdot a\)
Por fim, comparamos a força resultante antes e a força resultante nova, e observamos que:
\(F'=2 \cdot F\)
Resposta Questão 2
Alternativa E.
Calcularemos a massa da barra por meio da fórmula da alavanca:
\(F_p \cdot d_p = F_r \cdot d_r\)
Nesse caso a força resistente é a força peso sobre o arroz e a força potente é a força peso:
\(P_p \cdot d_p = P_{\text{arroz}} \cdot d_{\text{arroz}}\)
\(m_p \cdot g \cdot d_p = m_{\text{arroz}} \cdot g \cdot d_{\text{arroz}}\)
\(m_p \cdot 10 \cdot 1 = 5 \cdot 10 \cdot 3 \)
\(m_p \cdot 10 \cdot 1 = 5 \cdot 10 \cdot 3\)
\(m_p \cdot 10 = 150 \)
\(m_p = \frac{150}{10}\)
\(m_p = 15 \, \text{kg} \)
Resposta Questão 3
Alternativa C.
A velocidade de escoamento do fluido é inversamente proporcional a sua área de seção de escoamento e pressão, então no ponto 1 temos uma menor velocidade e maior pressão.
Resposta Questão 4
Alternativa D.
O som não se propaga no vácuo, já que se trata de uma onda material.
Resposta Questão 5
Alternativa A.
Primeiramente, transformaremos os minutos em segundos:
\(5 min \cdot 60s = 300 s\)
Por fim, calcularemos a aceleração média através da sua fórmula:
\(a_m = \frac{\Delta v}{\Delta t}\)
\(a_m = \frac{60}{300} \)
\(a_m = 0{,}2 \, \text{m/s}^2\)
Resposta Questão 6
Alternativa C.
Calcularemos a área 2 através da equivalência entre as suas pressões e a fórmula da pressão:
\(p_1=p_2\)
\(\frac{F_1}{A_1} = \frac{F_2}{A_2}\)
\(\frac{2000}{4} = \frac{10000}{A_2}\)
\(A_2 = \frac{10000 \cdot 4}{2000} \)
\(A_2=20 m^2\)
Resposta Questão 7
Alternativa E.
Calcularemos a força resultante no corpo através da fórmula da segunda lei de Newton:
\(F=m \cdot a\)
\(F=100 \cdot 5\)
\(F=500 N\)
Resposta Questão 8
Alternativa B.
Primeiramente, calcularemos o centro de massa no eixo x:
\(x_{\text{CM}} = \frac{m_1 \cdot x_1 + m_2 \cdot x_2 + m_3 \cdot x_3}{m_1 + m_2 + m_3} \)
\(x_{\text{CM}} = \frac{0{,}1 \cdot 0 + 0{,}1 \cdot (-3) + 0{,}1 \cdot 4}{0{,}1 + 0{,}1 + 0{,}1} \)
\(x_{\text{CM}} = \frac{0 - 0{,}3 + 0{,}4}{0{,}3} \)
\(x_{\text{CM}} = \frac{0{,}1}{0{,}3}\)
\(x_{\text{CM}} = \frac{1}{3}\)
Por fim, calcularemos o centro de massa no eixo y:
\(y_{\text{CM}} = \frac{m_1 \cdot y_1 + m_2 \cdot y_2 + m_3 \cdot y_3}{m_1 + m_2 + m_3}\)
\(y_{\text{CM}} = \frac{0{,}1 \cdot 2 + 0{,}1 \cdot 1 + 0{,}1 \cdot 0}{0{,}1 + 0{,}1 + 0{,}1} \)
\(y_{\text{CM}} = \frac{0{,}2 + 0{,}1 + 0}{0{,}3}\)
\(y_{\text{CM}} = \frac{0{,}3}{0{,}3} \)
\(y_{CM}=1\)
Resposta Questão 9
Alternativa A.
Calcularemos a área da seção de escoamento no ponto 1, através da equação da continuidade:
\(A_A \cdot v_A = A_B \cdot v_B\)
\(A_A \cdot 4 = 2 \cdot 10\)
\(A_A = \frac{20}{4} \)
\(A_A=5 m^2\)
Resposta Questão 10
Alternativa D.
Na teoria da relatividade estudamos a teoria da relatividade geral e a teoria da relatividade restrita, nas quais estudamos a dilatação do tempo, o princípio da simultaneidade e outros assuntos.
Resposta Questão 11
Alternativa B.
Calcularemos a velocidade angular média através da sua fórmula:
\(\omega_m = \frac{\Delta \varphi}{\Delta t}\)
\(\omega_m = \frac{\varphi_f - \varphi_i}{\Delta t} \)
\(\omega_m = \frac{10 - 2}{2}\)
\(\omega_m = \frac{8}{2}\)
\(ω_m=4 rad/s\)
Resposta Questão 12
Alternativa E.
Calcularemos a variação de pressão sobre o mergulhador através da fórmula do teorema de Stevin:
\(∆p=ρ \cdot g \cdot ∆h\)
\(∆p=1000 \cdot 10 \cdot 2\)
\(∆p=20000\)
\(∆p=2 \cdot 10^4 Pa\)
