Questão 1
(UEL) Uma mola, submetida à ação de uma força de intensidade 10 N , está deformada de 2,0 cm . O módulo do trabalho realizado pela força elástica na deformação de 0 a 2,0 cm foi, em joules, de:
A) 0,1.
B) 0,2.
C) 0,5.
D) 1,0.
E) 2,0.
Questão 2
(Uern) A tabela apresenta a força elástica e a deformação de 3 molas diferentes. Comparando-se as constantes elásticas destas 3 molas, tem-se que:
|
Mola |
Força Elástica (N) |
Deformação (m) |
|
1 |
400 |
0,50 |
|
2 |
300 |
0,300 |
|
3 |
600 |
0,8 |
A) \(k_1>k_2>k_3.\)
B) \(k_2>k_1>k_3.\)
C) \(k_2>k_3>k_1.\)
D) \(k_3>k_2>k_1.\)
Questão 3
(Mackenzie - adaptado) O conjunto mostrado está em movimento devido à ação da força horizontal de 50 N. Despreze os atritos. O coeficiente de elasticidade da mola ideal que está entre os blocos A e B, de massas respectivamente iguais a 6 kg e 4 kg, é 1.000 N/m. A deformação sofrida pela mola é:
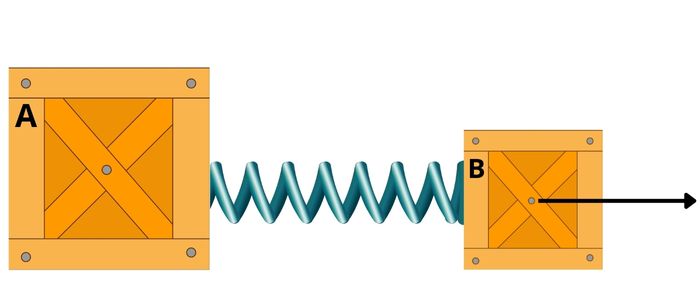
A) 2 cm.
B) 4 cm.
C) 5 cm.
D) 7 cm.
E) 10 cm.
Questão 4
(Unicamp) Assinale as afirmativas verdadeiras e as afirmativas falsas.
( ) As molas são distendidas uniformemente por forças que variam com a distância.
( ) A expressão da força que distende a mola de constante K é \(F\ =\ K\cdot x\), onde x é o alongamento da mola.
( ) A mola do item anterior reage sempre com força \(F\prime\ =\ -K\cdot x\) , onde x é o alongamento da mola.
( ) Os dinamômetros são equipamentos destinados a medir forças.
( ) Nos sistemas conservativos, a energia mecânica é conservada.
Questão 5
Uma mola com uma constante elástica que vale 250 N/cm é deformada em 5 cm , a partir disso, determine qual deve ser a força elástica aplicada sobre ela.
A) 1,25 N
B) 12 500 N
C) 1250 N
D) 125 N
E) 12,5 N
Questão 6
Qual a força elástica sofrida por uma mola de constante elástica 100 N/m quando é comprimida em 10 cm ?
A) 7 N
B) 8 N
C) 9 N
D) 10 N
E) 11 N
Questão 7
Determine o trabalho realizado pela força elástica para deformar uma mola em 25 cm , sabendo que ela possui uma constante elástica de 500 N/m .
A) 15,625 J
B) 156,25 J
C) 1,5625 J
D) 1562,5 J
E) 0,15625 J
Questão 8
Qual a elongação sofrida por uma mola que apresenta uma constante elástica de 2 kN/m e é puxada com uma força de 400 N ?
A) 0,1
B) 0,2
C) 0,3
D) 0,4
E) 0,5
Questão 9
Uma mola com força elástica \(F_{el\ 1}\) , possui constante elástica k e elongação duas vezes maior que a de uma outra mola, que tem constante elástica 4k e força elástica \(F_{el\ 2}\) . A partir disso, determine a relação entre as duas forças elásticas.
A) \(F_{el\ 2}=\frac{F_{el\ 1}}{2}\)
B) \(F_{el\ 2}=\frac{F_{el\ 1}}{8}\)
C) \(F_{el\ 2}=2\cdot F_{el\ 1}\)
D) \(F_{el\ 2}=4\cdot F_{el\ 1}\)
E) \( F_{el\ 2}=8\cdot F_{el\ 1}\)
Questão 10
Uma mola sofreu uma força de intensidade quatro vezes maior que a força inicial aplicada, mantendo a sua constante elástica da mola. Em vista disso, compare a elongação final da mola com a elongação inicial da mola.
A) \(x_{final}=\frac{{\ x}_{inicial}}{2}\)
B) \(x_{final}=\frac{{\ x}_{inicial}}{4}\)
C) \(x_{final}=2\cdot{\ x}_{inicial}\)
D) \(x_{final}=4\cdot{\ x}_{inicial}\)
E) \(x_{final}={\ x}_{inicial}\)
Questão 11
Sabendo que, na Física, muitas vezes nomeamos equações, unidades de medida e leis para homenagear grandes físicos ainda que eles não as tenham desenvolvido, responda: quem foi o físico responsável pela fórmula da força elástica?
A) Robert Hooke.
B) Galileu Galilei.
C) Giordano Bruno.
D) Robert Boyle.
E) Isaac Newton.
Questão 12
Quais proposições apresentam a unidade de medida correspondente à grandeza física estudada em força elástica?
I. A constante elástica é medida em Newton.
II. A força elástica é medida em Newton.
III. A elongação da mola é medida em Joule.
IV. O trabalho da força elástica é medida em Joule.
V. A aceleração é medida em metros por segundo.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e V.
D) Alternativas II e III.
E) Alternativas II e IV.
Resposta Questão 1
Alternativa A.
Primeiramente, vamos converter a deformação sofrida pela mola de centímetros para metros:
\(2\ cm=0,02\ m\)
Calcularemos a constante da mola utilizando a fórmula da força elástica:
\(F_{el}=\ k\cdot x\)
\(10=\ k\cdot0,02\)
\(k=\frac{10}{0,02}\)
\(k=500\ N/m\)
Por fim, vamos calcular o trabalho realizado pela força elástica a partir da sua fórmula:
\(W_{el}=\frac{{k\cdot x}^2}{2}\)
\(W_{el}=\frac{{500\cdot0,02}^2}{2}\)
\(W_{el}=\frac{500\cdot0,0004}{2}\)
\(W_{el}=0,1\ J\)
Resposta Questão 2
Alternativa B.
Calcularemos a constante de cada mola através da fórmula da força elástica:
\(F_{el}=\ k\cdot∆x\)
Mola 1:
\(F_{el}=\ k_1\cdot∆x\)
\(400=k_1\cdot0,5\)
\(k_1=\frac{400}{0,5}\)
\(k_1=800\ N/m\)
Mola 2:
\(F_{el}=\ k_2\cdot∆x\)
\(300=k_2\cdot0,3\)
\(=\frac{300}{0,3}\)
\(k_2=1000\ N/m\)
Mola 3:
\(F_{el}=\ k_3\cdot∆x\)
\(600=k_3\cdot0,8\)
\(k_3=\frac{600}{0,8}\)
\(k_3=750\ N/m\)
Então:
\(k_2>k_1>k_3\)
Resposta Questão 3
Alternativa A.
Primeiramente, calcularemos a aceleração do sistema a partir da fórmula da força resultante:
\(F_R=m\cdot a\)
A força resultante será a força horizontal e a massa será o somatório entre as massas dos blocos:
\(F_R=(M+m)\cdot a\)
\(50=(6+4)\cdot a\)
\(50=10\cdot a\)
\(a=\frac{50}{10}\)
\(a=5\ m/s^2\ \)
Finalmente, vamos calcular a deformação sofrida pela mola no bloco a, já que a única força atuando sobre esse bloco é a força elástica, então usaremos a fórmula da força resultante:
\(F_R=m\cdot a\)
\(F_{el}=m\cdot a\)
\(k\cdot x=m\cdot a\)
\(1000\cdot x=4\cdot5\)
\(1000\cdot x=20\)
\(x=\frac{20}{1000}\)
\(x=0,02\ m\)
0,02 metros equivale a 2 cm.
Resposta Questão 5
Alternativa C.
Nesse caso, não há necessidade de converter a unidade de medida da elongação, já que a constante da mola também está em centímetros. Então, calcularemos a força elástica através da sua fórmula:
\(F_{el}=\ k\cdot∆x\)
\(F_{el}=\ 250\cdot5\)
\(F_{el}=\ 1250\ N\)
Resposta Questão 6
Alternativa D.
Primeiramente, converteremos a elongação de centímetro para metro:
\(10\ cm=0,1\ m\)
Vamos calcular a força elástica através da sua fórmula:
\(F_{el}=\ k\cdot∆x\)
\(F_{el}=\ 100\cdot0,1\)
\(F_{el}=\ 10\ N\)
Resposta Questão 7
Alternativa A.
Primeiramente, converteremos a elongação de centímetro para metro:
\(25\ cm=0,25\ m\)
Depois, vamos calcular o trabalho realizado pela força elástica a partir da sua fórmula:
\(W_{el}=\frac{{k\cdot x}^2}{2}\)
\(W_{el}=\frac{{500\cdot0,25}^2}{2}\)
\(W_{el}=\frac{500\cdot0,0625}{2}\)
\(W_{el}=\frac{500\cdot0,0625}{2}\)
\(W_{el}=15,625\ J\)
Resposta Questão 8
Alternativa B.
Sabendo que o k significa kilo e equivale a 103 , então a constante elástica vale:
\(2\ k=2\cdot{10}^3=2000\ N/m\)
Calcularemos a elongação da mola através da fórmula da força elástica:
\(F_{el}=\ k\cdot∆x\)
\(400=\ 2000\cdot∆x\)
\(\frac{400}{2000}=\ ∆x\)
\(0,2\ m=∆x\)
Resposta Questão 9
Alternativa C.
De acordo com as informações, a elongação da primeira mola é o dobro da elongação da segunda mola:
\(x_1=2\cdot x_2\)
Para determinarmos a relação entre as forças elásticas de cada mola, utilizaremos a fórmula da força elástica:
\(F_{el}=\ k\cdot x\)
A força elástica da mola 1:
\(F_{el\ 1}=k_1\cdot x_1\)
\(F_{el\ 1}=k\cdot2\cdot x_2\)
\(\frac{F_{el\ 1}}{2}=k\cdot x_2\)
A força elástica da mola 2:
\(F_{el\ 2}=k_2\cdot x_2\)
\(F_{el\ 2}=4\cdot k\cdot x_2\)
Substituindo o lugar de k∙x2 pelo valor obtido da força elástica da mola 1:
\(F_{el\ 2}=4\cdot\frac{F_{el\ 1}}{2}\)
\(F_{el\ 2}=2\cdot F_{el\ 1}\)
Portanto, a força elástica da mola 2 é o dobro da força elástica da mola 1.
Resposta Questão 10
Alternativa D.
A força elástica inicial é calculada pela fórmula da força elástica:
\(F_{el\ }=k\cdot x\)
Como queremos a comparação entre as elongações da mola, isolaremos o seu termo:
\(x=\frac{F_{el\ }}{k}\)
A partir dela, podemos perceber que a elongação da mola é proporcional à força elástica e inversamente proporcional à constante elástica da mola. Então, se a força aumentou em quatro vezes, a elongação da mola também aumentará em quatro vezes, já que a constante elástica da mola se manteve constante. Dessa forma, temos:
\(x_{final}=4\cdot{\ x}_{inicial}\)
Resposta Questão 11
Alternativa A.
A fórmula da força elástica, também chamada de lei de Hooke, foi desenvolvida por Robert Hooke.
Resposta Questão 12
Alternativa E.
I. A constante elástica é medida em Newton. (falso)
A constante elástica é medida em Newton por metros.
II. A força elástica é medida em Newton. (verdadeiro)
III. A elongação da mola é medida em Joule. (falso)
A elongação da mola é medida em metros.
IV. O trabalho da força elástica é medida em Joule. (verdadeiro)
V. A aceleração é medida em metros por segundo. (falso)
A aceleração é medida em metros por segundo ao quadrado.



