Questão 1
(Uerj - Adaptada) No mapa abaixo, está representada a variação média da temperatura dos oceanos em determinado mês do ano. Ao lado, encontra-se a escala, em graus Celsius, utilizada para a elaboração do mapa.
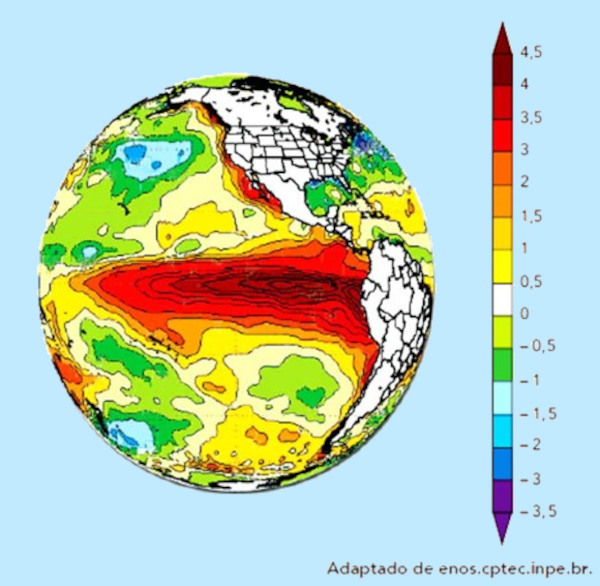
Determine, em graus Kelvin, o módulo da variação entre a maior e a menor temperatura da escala apresentada.
A) 6 K
B) 7 K
C) 8 K
D) 9 K
E) 10 K
Questão 2
(Uerj) Observe na tabela os valores das temperaturas dos pontos críticos de fusão e de ebulição, respectivamente, do gelo e da água, à pressão de 1 atm, nas escalas Celsius e Kelvin.
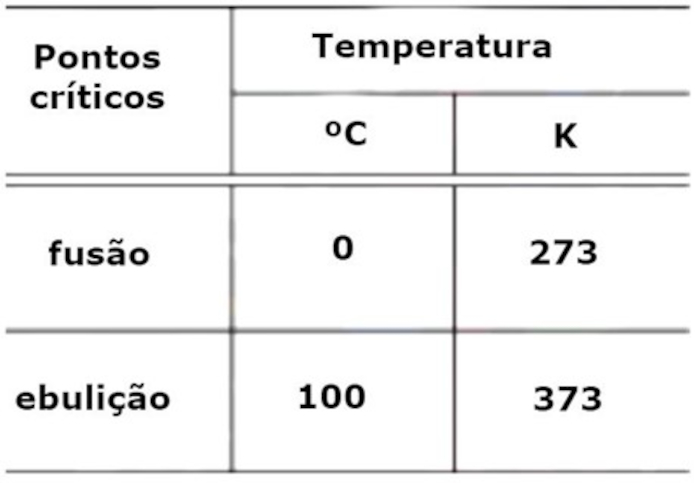
Considere que, no intervalo de temperatura entre os pontos críticos do gelo e da água, o mercúrio em um termômetro apresenta uma dilatação linear. Nesse termômetro, o valor na escala Celsius correspondente à temperatura de 313 K é igual a:
A) 20
B) 30
C) 40
D) 60
Questão 3
(Senac) A chegada do homem à lua aconteceu em 1969. A estrutura da lua é rochosa e praticamente não possui atmosfera, o que faz com que durante o dia a temperatura chegue a 105 °C e à noite caia para −155 °C. Essa variação térmica, medida na escala Fahrenheit de temperatura, vale:
A) 50.
B) 90.
C) 292.
D) 468.
E) 472.
Questão 4
(PUC) O Slide, nome dado ao skate futurista, usa levitação magnética para se manter longe do chão e ainda ser capaz de carregar o peso de uma pessoa. É o mesmo princípio utilizado, por exemplo, pelos trens ultrarrápidos japoneses.
Para operar, o Slide deve ter a sua estrutura metálica interna resfriada a temperaturas baixíssimas, alcançadas com nitrogênio líquido. Daí a “fumaça” que se vê nas imagens, que, na verdade, é o nitrogênio vaporizando novamente devido à temperatura ambiente e que, para permanecer no estado líquido, deve ser mantido a aproximadamente –200 graus Celsius. Então, quando o nitrogênio acaba, o skate para de “voar”.

Fumaça que aparenta sair do skate, na verdade, é nitrogênio em gaseificação (Foto: Divulgação/Lexus)
Fonte: www.techtudo.com.br/noticias/noticia/2015/07/como-funciona-o-skate-voador-inspirado-no-filme-de-volta-para-o-futuro- 2.html. Consultado em: 03/07/2015
Com relação ao texto, a temperatura do nitrogênio o líquido, –200 °C, que resfria a estrutura metálica interna do Slide, quando convertida para as escalas Fahrenheit e Kelvin, seria respectivamente:
A) –328 e 73
B) –392 e 73
C) –392 e –473
D) –328 e –73
Questão 5
Transforme a temperatura 33,15 K para a escala Fahrenheit.
A) - 800 ℉
B) - 400 ℉
C) 0 ℉
D) 400 ℉
E) 800 ℉
Questão 6
Um estudante de intercâmbio chegou aos Estados Unidos da América e verificou que a temperatura naquele dia era de 64,4 ºF. Ele ficou em dúvida já que em seu país a temperatura é medida em Celsius, então ele realizou a conversão através da calculadora. Qual valor ele encontrou?
A) 10 ℃
B) 12 ℃
C) 14 ℃
D) 16 ℃
E) 18 ℃
Questão 7
A temperatura máxima registrada em um dia de verão foi de 313 K e a temperatura máxima registrada em um dia de inverno foi de 268 K. Por meio dessas informações, calcule a variação de temperatura em Celsius:
A) -5 ºC
B) 0 ºC
C) 40 ºC
D) 45 ºC
E) 80 ºC
Questão 8
Uma cientista precisa que a temperatura da substância esteja na escala Kelvin. Sabendo que a temperatura da substância é de 80,6 ºF, encontre o seu valor na escala Kelvin.
A) 300 K
B) 324 K
C) 356 K
D) 373 K
E) 400 K
Questão 9
Sabendo que a temperatura de fusão da água é 273 K, quanto é essa temperatura na escala Fahrenheit?
A) 0 ℉
B) 32 ℉
C) 85 ℉
D) 120 ℉
E) 273 ℉
Questão 10
Transforme a temperatura 14 ºF para a escala Celsius.
A) 10 ℃
B) 20 ℃
C) 0 ℃
D) -20 ℃
E) -10 ℃
Questão 11
Em um laboratório, uma substância apresenta a temperatura de 353 K. Quanto é essa temperatura na escala Celsius?
A) 60 ℃
B) 70 ℃
C) 80 ℃
D) 90 ℃
E) 100 ℃
Questão 12
Em um dia de inverno, a temperatura marcada é de 40 ºF. Quanto é essa temperatura na escala Kelvin?
A) 278 K
B) 280 K
C) 282 K
D) 284 K
E)  286 K
286 K
Resposta Questão 1
Alternativa C.
Calcularemos a variação da temperatura na escala Celsius entre a maior temperatura, de 4,5 ºC, e a menor temperatura, de -3,5 ºC:
\(\Delta T_C = 4,5 - (-3,5) \)
\(∆T_C=8 ℃\)
A variação da temperatura na escala Celsius é igual à variação da temperatura na escala Kelvin, então o módulo da variação entre a maior e a menor temperatura da escala apresentada é de 8 K.
Resposta Questão 2
Alternativa C.
Converteremos a temperatura na escala Kelvin para a escala Celsius, através da fórmula:
\(T_C = T_K - 273 \)
\(T_C = 313 - 273 \)
\(T_C = 40 \, ^\circ \text{C} \)
Resposta Questão 3
Alternativa D.
Primeiramente, converteremos a temperatura mais alta da escala Celsius para a escala Fahrenheit, através da fórmula:
\(\frac{T_C}{5} = \frac{T_F - 32}{9} \)
\(\frac{105}{5} = \frac{T_F - 32}{9} \)
\(21 = \frac{T_F - 32}{9} \)
\(T_F - 32 = 21 \cdot 9 \)
\(T_F - 32 = 189 \)
\(T_F = 189 + 32\)
\(T_F=221 ℉\)
Em seguida, converteremos a temperatura mais baixa da escala Celsius para a escala Fahrenheit, através da fórmula:
\(\frac{T_C}{5} = \frac{T_F - 32}{9}\)
\(\frac{-155}{5} = \frac{T_F - 32}{9} \)
\(-31 = \frac{T_F - 32}{9} \)
\(T_F-32=-31 \cdot 9\)
\(T_F - 32 = -279 \)
\(T_F = -279 + 32 \)
\(T_F = -247 \, ^\circ \text{F} \)
Por fim, calcularemos a variação de temperatura na escala Fahrenheit:
\(\Delta T_F = 221 - (-247) \)
\(\Delta T_F = 468 \)
Resposta Questão 4
Alternativa A.
Primeiramente, converteremos a temperatura na escala Celsius para a escala Fahrenheit:
\(\frac{T_C}{5} = \frac{T_F - 32}{9}\)
\(\frac{-200}{5} = \frac{T_F - 32}{9} \)
\(-40 = \frac{T_F - 32}{9} \)
\(T_F-32=-40 \cdot 9\)
\(T_F-32=-360\)
\(T_F=-360+32\)
\(T_F=-328 ℉\)
Por fim, converteremos a temperatura na escala Celsius para a escala Kelvin:
\(T_C=T_K-273\)
\(-200=T_K-273\)
\(T_K=-200+273\)
\(T_K = 73 \, \text{K} \)
Resposta Questão 5
Alternativa B.
Converteremos a temperatura na escala Kelvin para a escala Fahrenheit:
\(\frac{T_F - 32}{9} = \frac{T_K - 273}{5} \)
\(\frac{T_F - 32}{9} = \frac{33 - 273}{5} \)
\(\frac{T_F - 32}{9} = \frac{-240}{5} \)
\(\frac{T_F - 32}{9} = -48 \)
\(T_F - 32 = -48 \cdot 9 \)
\(T_F-32=-432\)
\(T_F = -432 + 32 \)
\(T_F=-400 ℉\)
Resposta Questão 6
Alternativa E.
Converteremos a temperatura na escala Fahrenheit para a escala Celsius:
\(\frac{T_C}{5} = \frac{T_F - 32}{9} \)
\(\frac{T_C}{5} = \frac{64,4 - 32}{9} \)
\(\frac{T_C}{5} = \frac{32,4}{9} \)
\(\frac{T_C}{5} = 3,6 \)
\(T_C=3,6 \cdot 5\)
\(T_C=18 ℃\)
Resposta Questão 7
Alternativa D.
Calcularemos a variação da temperatura na escala Kelvin entre a maior temperatura, de 313 K, e a menor temperatura, de 268 K:
\(∆T_K=313-268\)
\(∆T_K=45 K\)
A variação da temperatura na escala Kelvin é igual à variação da temperatura na escala Celsius, então o módulo da variação entre a maior e a menor temperatura da escala apresentada é de 45 ºC.
Resposta Questão 8
Alternativa A.
Converteremos a temperatura na escala Fahrenheit para a escala Kelvin:
\(\frac{T_F - 32}{9} = \frac{T_K - 273}{5} \)
\(\frac{80,6 - 32}{9} = \frac{T_K - 273}{5}\)
\(\frac{48,6}{9} = \frac{T_K - 273}{5} \)
\(5,4 = \frac{T_K - 273}{5} \)
\(T_K-273=5,4 \cdot 5\)
\(T_K-273=27\)
\(T_K=27+273\)
\(T_K=300 K\)
Resposta Questão 9
Alternativa B.
Converteremos a temperatura na escala Kelvin para a escala Fahrenheit:
\(\frac{T_F - 32}{9} = \frac{T_K - 273}{5} \)
\(\frac{T_F - 32}{9} = \frac{273 - 273}{5} \)
\(\frac{T_F - 32}{9} = \frac{0}{5} \)
\(\frac{T_F - 32}{9} = 0 \)
\(T_F-32=0 \cdot 9\)
\(T_F-32=0\)
\(T_F=0+32\)
\(T_F=32 ℉ \)
Resposta Questão 10
Alternativa E.
Converteremos a temperatura na escala Fahrenheit para a escala Celsius:
\(\frac{T_C}{5} = \frac{T_F - 32}{9} \)
\(\frac{T_C}{5} = \frac{14 - 32}{9}\)
\(\frac{T_C}{5} = \frac{-18}{9}\)
\(\frac{T_C}{5} = -2\)
\(T_C=-2 \cdot 5\)
\(T_C=-10 ℃\)
Resposta Questão 11
Alternativa C.
Converteremos a temperatura na escala Kelvin para a escala Celsius:
\(T_C=T_K-273\)
\(T_C=353-273\)
\(T_C=80 ℃\)
Resposta Questão 12
Alternativa A.
Converteremos a temperatura na escala Fahrenheit para a escala Kelvin:
\(\frac{T_F - 32}{9} = \frac{T_K - 273}{5}\)
\(\frac{41 - 32}{9} = \frac{T_K - 273}{5} \)
\(\frac{9}{9} = \frac{T_K - 273}{5}\)
\(1 = \frac{T_K - 273}{5}\)
\(T_K - 273 = 1 \cdot 5 \)
\(T_K-273=5\)
\(T_K=5+273\)
\(T_K=278 K\)




