Questão 1
(Espcex – Aman) O desenho abaixo representa um circuito elétrico composto por resistores ôhmicos, um gerador ideal e um receptor ideal.
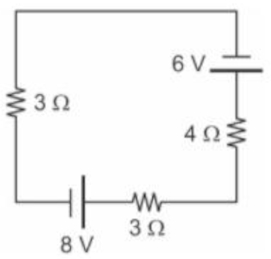
A potência elétrica dissipada no resistor de 4Ω do circuito é:
a) 0,16W
b) 0,20W
c) 0,40W
d) 0,72W
e) 0,80W
Questão 2
(Uneb-BA) Um resistor ôhmico, quando submetido a uma ddp de 40V, é atravessado por uma corrente elétrica de intensidade 20A. Quando a corrente que o atravessa for igual a 4A, a ddp, em volts, nos seus terminais, será:
a) 8
b) 12
c) 16
d) 20
e) 30
Questão 3
(Mackenzie)
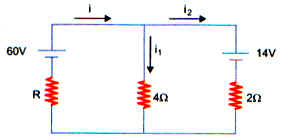
Alt: Circuito elétrico com três malhas percorridas por corrente elétrica.
Título: circuito-eletrico-exercicios-corrente
No circuito acima, o gerador e o receptor são ideais e as correntes têm os sentidos indicados. Se a intensidade da corrente i1 é 5A, então o valor da resistência do resistor R é:
a) 8Ω
b) 5Ω
c) 4Ω
d) 6Ω
e) 3Ω
Questão 4
(UEL) Um resistor de \(10Ω\) no qual flui uma corrente elétrica de 3,0 ampères está associado em paralelo com outro resistor. Sendo a corrente elétrica total, na associação, igual a 4,5 ampères, o valor do segundo resistor, em Ohms, é:
a) 5,0
b) 10
c) 20
d) 30
e) 60
Questão 5
Determine a tensão elétrica em um circuito elétrico que é atravessado por uma corrente elétrica de 2,5 A que dissipa uma potência elétrica de 500W.
a) 50V
b) 100V
c) 150V
d) 200V
e) 250V
Questão 6
Calcule a capacitância equivalente em um circuito elétrico composto de três capacitores de capacitância \(5mF\), sabendo que dois eles estão associados em paralelo e um deles está associado em série.
Dica: Calcule primeiro a capacitância equivalente na associação em série e depois na associação em paralelo.
a) 2,5mF
b) 3,0mF
c) 4,5mF
d) 5,0mF
e) 7,5mF
Questão 7
Calcule a resistência equivalente em um circuito elétrico composto de quatro resistores, com três deles de resistência elétrica igual \(2Ω\) a associados em série e um deles de resistência elétrica igual a \(4Ω\) associado em paralelo com os outros.
Dica: Calcule primeiro a resistência equivalente na associação em série e depois na associação em paralelo.
a) 2,4Ω
b) 4,8Ω
c) 7,2Ω
d) 9,6Ω
e) 12,0Ω
Questão 8
Dentre as alternativas abaixo, qual não se trata de um tipo de circuito elétrico?
I. Circuito elétrico simples.
II. Circuito elétrico com elementos associados em série.
III. Circuito elétrico complexo.
IV. Circuito elétrico com elementos associados em série.
V. Circuito elétrico sem corrente elétrica.
a) Alternativa I.
b) Alternativa II.
c) Alternativa III.
d) Alternativa IV.
e) Alternativa V.
Questão 9
Calcule a corrente elétrica que percorre um circuito elétrico que tem um resistor de resistência elétrica \(22Ω\) e uma bateria de 110V.
a) 1A
b) 3A
c) 5A
d) 7A
e) 9A
Questão 10
Em um circuito elétrico temos um gerador elétrico que tem uma resistência elétrica interna de \(4Ω\) que é atravessado por uma corrente elétrica de 3A quando conectado a uma ddp de 20V; sabendo disso, calcule a força eletromotriz (f.e.m.) desse gerador elétrico.
a) 8V
b) 16V
c) 27V
d) 32V
e) 45V
Questão 11
O circuito elétrico de uma rede elétrica possui um resistor de resistência elétrica R que quando conectado a uma tensão elétrica de 300V é percorrido por uma corrente elétrica de 5ª. Com base nessas informações, calcule a resistência elétrica desse resistor.
a) 50Ω
b) 60Ω
c) 70Ω
d) 80Ω
e) 90Ω
Questão 12
Quais das alternativas apresentam as unidades de medidas correspondentes às grandezas físicas estudadas nos circuitos elétricos?
I. A resistência elétrica é medida em Ohm por metro.
II. A corrente elétrica é medida em Ampère.
III. A tensão elétrica é medida em Volt.
IV. A potência elétrica é medida em Volt.
a) Alternativas I e II.
b) Alternativas III e IV.
c) Alternativas I e V.
d) Alternativas II e III.
e) Alternativas II e IV.
Resposta Questão 1
LETRA A
Nesse circuito elétrico temos uma malha composta por uma única corrente elétrica, portanto não será necessário utilizarmos a lei dos nós, então adotaremos o sentido da corrente elétrica e da malha como anti-horário.
Iniciando a partir do resistor 3Ω, calcularemos a corrente elétrica usando a lei das malhas de Kirchhoff:
\(+3i-8+3i+4i+6=0\)
\(+10i-2=0\)
\(10i=2\)
\(i = \frac{2}{10} \)
\(i=0,2A\)
Por fim, calcularemos a potência elétrica dissipada nesse resistor através da sua fórmula:
\(P = U \cdot i \)
\(P=0,8\cdot0,2\)
\(P=0,16W\)
Resposta Questão 2
LETRA A
Primeiramente, calcularemos a resistência elétrica do resistor, através da fórmula da 1ª lei de Ohm:
\(U = R \cdot i \)
\(40=R\cdot20\)
\(R = \frac{40}{20} \)
\(R=2Ω\)
Depois, calcularemos a tensão elétrica quando esse resistor é percorrido pela corrente elétrica de 4A, através da fórmula da 1ª lei de Ohm:
\(U = R \cdot i \)
\(U=2\cdot4\)
\(U=8V\)
Resposta Questão 3
LETRA B
Nesse circuito elétrico temos três malhas percorridas por três correntes elétricas, então adotaremos o sentido das correntes elétricas e das malhas como horário.
Iniciando a partir da tensão elétrica de 14V na malha 2, a direita, calcularemos a corrente elétrica usando a lei das malhas de Kirchhoff:
\(14 + 2i_{2} - 4i_{1} = 0 \)
\(14 + 2i_{2} - 4 \cdot 5 = 0 \)
\(14 + 2i_{2} - 20 = 0 \)
\(2i_{2} - 6 = 0 \)
\(2i_{2} = 6 \)
\(i_{2} = \frac{6}{2} \)
\(i_{2} = 3 \, \text{A} \)
Iniciando a partir resistência elétrica de \(4Ω\) na malha 1, a esquerda, usando a lei das malhas de Kirchhoff obteremos a expressão algébrica:
\(+4i_{1} + Ri - 60 = 0 \)
\(+4 \cdot 5 + Ri - 60 = 0 \)
\(20 + Ri - 60 = 0 \)
\(Ri-40=0\)
\(Ri=40\)
Usando a lei dos nós, calcularemos a corrente elétrica i:
\(i = i_{1} + i_{2} \)
\(i=5+3\)
\(i=8A\)
E por fim, calcularemos a resistência do resistor R, usando a expressão obtida através da malha 1:
\(Ri=40\)
\(R\cdot8=40\)
\(R = \frac{40}{8} \)
\(R=5Ω\)
Resposta Questão 4
LETRA C
Primeiramente, calcularemos nesse circuito elétrico a tensão elétrica no resistor de \(10Ω\) percorrido pela corrente de \(3A\), através da fórmula da 1ª lei de Ohm:
\(U=R\cdot i\)
\(U=10\cdot3\)
\(U=30V\)
O primeiro e o segundo resistores estão associados paralelamente, então as suas tensões elétricas são iguais, assim calcularemos a resistência do segundo resistor, novamente através da fórmula da 1ª lei de Ohm:
\(U=R\cdot i\)
Lembrando que a corrente elétrica do segundo resistor é a subtração da corrente elétrica total e a corrente elétrica do primeiro resistor:
\(30 = R \cdot (4,5 - 3) \)
\(30 = R \cdot 1,5 \)
\(R = \frac{30}{1,5} \)
\(R=20Ω\)
Resposta Questão 5
LETRA D
Calcularemos a tensão elétrica nesse circuito elétrico através da fórmula de potência elétrica dissipada:
\(P = U \cdot i \)
\(500 = U \cdot 2,5 \)
\(U = \frac{500}{2,5} \)
\(U=200V\)
Resposta Questão 6
LETRA E
Primeiramente, calcularemos a capacitância equivalente dessa associação em série, através da sua fórmula:
\(C_{12} = \frac{C_{1} \cdot C_{2}}{C_{1} + C_{2}} \)
\(C_{12} = \frac{5 \cdot 5}{5 + 5} \)
\(C_{12} = \frac{25}{10} \)
\(C_{12} = 2,5 \, \text{mF} \)
Por fim, calcularemos a capacitância equivalente na associação em paralelo, através da soma de todas as capacitâncias:
\(C_{\text{eq}} = C_{3} + C_{12} \)
\(C_{\text{eq}} = 5 + 2,5 \)
\(C_{\text{eq}} = 7,5 \, \text{mF} \)
Resposta Questão 7
LETRA A
Primeiramente, calcularemos a resistência elétrica equivalente entre os resistores associados em série através da soma de todas as resistências elétricas:
\(R_{123} = R_{1} + R_{2} + R_{3} \)
\(R_{123} = 2 + 2 + 2 \)
\(R_{123} = 6 \, \Omega \)
Por fim, calcularemos a resistência elétrica equivalente dos resistores associados em paralelo através da fórmula:
\(R_{\text{eq}} = \frac{R_{123} \cdot R_{4}}{R_{123} + R_{4}} \)
\(R_{\text{eq}} = \frac{6 \cdot 4}{6 + 4} \)
\(R_{\text{eq}} = \frac{24}{10} \)
\(R_{\text{eq}} = 2,4 \, \Omega \)
Resposta Questão 8
LETRA E
Os circuitos elétricos podem ser simples, quando atravessados por uma corrente elétrica; complexos, quando atravessados por mais de uma corrente elétrica; com elementos associados em série, em paralelo ou mistos.
Resposta Questão 9
LETRA C
Calcularemos a corrente elétrica que atravessa esse circuito elétrico através da fórmula da 1ª lei de Ohm:
\(U=R\cdot i\)
\(110=22\cdot i\)
\(i = \frac{110}{22} \)
\(i=5A \)
Resposta Questão 10
LETRA D
Calcularemos a força eletromotriz desse gerador elétrico, através da equação do gerador elétrico:
\(U = \varepsilon - r \cdot i \)
\(20 = \varepsilon - 4 \cdot 3 \)
\(20 = \varepsilon - 12 \)
\(\varepsilon = 20 + 12 \)
\(ε=32V\)
Resposta Questão 11
LETRA B
Calcularemos a resistência elétrica do resistor nesse circuito elétrico através da 1ª lei de Ohm:
\(R = \frac{U}{i} \)
\(R = \frac{300}{5} \)
\(R=60Ω\)
Resposta Questão 12
LETRA D
Apenas as alternativas II e III estão corretas. Abaixo, em vermelho, vemos a correção das alternativas.
I. Incorreta. A resistência elétrica é medida em Ohm.
II. Correta.
III. Correta.
IV. Incorreta. A potência elétrica é medida em Watt.



