Questão 1
(FCC) Qual é a velocidade escalar média, em km/h, de uma pessoa que percorre a pé 1200 m em 20 min?
A) 4,8
B) 3,6
C) 2,7
D) 2,1
E) 1,2
Questão 2
(Unesp) Um foguete lançador de satélites, partindo do repouso, atinge a velocidade de 5400 km/h após 50 segundos. Supondo que esse foguete se desloque em trajetória retilínea, sua aceleração escalar média é de
A) 30 m/s².
B) 150 m/s².
C) 388 m/s².
D) 108 m/s².
E) 54 m/s².
Questão 3
(FPS) Um automóvel percorre uma rodovia com velocidade inicialmente constante igual a 80 km/h. O motorista do veículo avista um radar e reduz sua velocidade para 60 km/h, percorrendo nesse trajeto uma distância igual a 20 m. O módulo da desaceleração sofrida pelo automóvel nesse percurso foi de aproximadamente:
A) 5,4 m/s²
B) 7,5 m/s²
C) 2,5 m/s²
D) 11 m/s²
E) 15 m/s²
Questão 4
(Uern) Seja o gráfico da velocidade em função do tempo de um corpo em movimento retilíneo uniformemente variado representado abaixo.
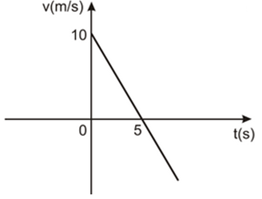
Considerando a posição inicial desse movimento igual a 46 m, então a posição do corpo no instante t = 8 s é
A) 54 m.
B) 62 m.
C) 66 m.
D) 74 m.
Questão 5
Um corpo inicialmente parado começa a se movimentar e após 10 s atinge a velocidade de 40\(\frac{m}{s}\).
A partir dessas informações, qual foi a aceleração desse corpo?
A) 2 m/s2
B) 2,5 m/s2
C) 3 m/s2
D) 3,5 m/s2
E) 4 m/s2
Questão 6
Qual das grandezas físicas descritas abaixo não é estudada na cinemática escalar?
A) Energia
B) Distância
C) Tempo
D) Velocidade
E) Aceleração
Questão 7
Calcule a velocidade média de um automóvel que se movimenta por uma avenida, passando pela posição de 40 metros aos 6 segundos e de 200 metros aos 10 segundos.
A) 10 m/s
B) 20 m/s
C) 30 m/s
D) 40 m/s
E) 50 m/s
Questão 8
Um carro esportivo parte do repouso e alcança uma velocidade de 216 km/h em 5 s . Sabendo disso, calcule a sua aceleração.
A) 6 m/s2
B) 10 m/s2
C) 12 m/s2
D) 16 m/s2
E) 18 m/s2
Questão 9
Calcule a variação de posição percorrida por um móvel que saiu do repouso e em 2 s atingiu a velocidade de 50 m/s, sabendo que a sua aceleração foi de 2 m/s.
A) 251 m
B) 349 m
C) 486 m
D) 513 m
E) 625 m
Questão 10
Quanto tempo um automóvel levou para deslocar 2000 metros, considerando que a sua aceleração foi de 40 m/s2 e que ele partiu do repouso?
A) 9 s
B) 10 s
C) 11 s
D) 12 s
E) 13 s
Questão 11
Uma bike speed alcançou uma velocidade final de 25 m/s após 5 segundos. Sabendo que a sua aceleração foi de 3 m/s2 , calcule a sua velocidade inicial.
A) 4 m/s
B) 6 m/s
C) 8 m/s
D) 10 m/s
E) 12 m/s
Questão 12
Quais das alternativas apresentam as unidades de medidas correspondentes às grandezas físicas estudadas na cinemática escalar?
I. A velocidade média é medida em metros por segundo.
II. O tempo é medido em segundos ao quadrado.
III. O deslocamento inicial é medido em metros por segundo.
IV. O deslocamento final é medido em metros.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e III.
D) Alternativas II e IV.
E) Alternativas I e IV.
Resposta Questão 1
Alternativa B.
Iniciaremos transformando o tempo de minutos para segundos:
\(t=20\min{=20\cdot60=1200\ s}\)
Depois, calcularemos a velocidade média em m/s através da sua fórmula:
\(v_m=\frac{Δx}{Δt}\)
\(v_m = \frac{1200\ m}{1200\ s} \)
\(v_m=1\ m/s\)
E finalizaremos transformando de m/s para km/h, multiplicando por 3,6:
\(v_m=1\ m/s\cdot3,6=3,6\ km/h\)
Resposta Questão 2
Alternativa A.
Iniciaremos transformando a velocidade de km/h para m/s:
\(\frac{5400\ km/h}{3.6} = 1500\ m/s \)
E finalizaremos calculando a aceleração média através da sua fórmula:
\(a_m = \frac{Δv}{Δt} \)
\(a_m = \frac{1500}{50} \)
\(a_m=30\ m/s^2\ \)
Resposta Questão 3
Alternativa A.
Iniciaremos transformando as velocidades de km/h para m/s:
\(\frac{80}{3,6}\cong22,22\ m/s\)
\(\frac{60}{3,6}\cong16,66\ m/s\)
E finalizaremos calculando a desaceleração através da fórmula de Torricelli:
\(v_f^2=v_i^2+2\cdot a\cdot∆x\)
\({16,66}^2={22,22}^2+2\cdot a\cdot20\)
\(277,77=493,82+40\cdot a\)
\(277,77-493,82\cong40\cdot a\)
\(-216,05\cong40\cdot a\)
\(a \approx -\frac{216.05}{40} \)
\(a\cong-5,40\ m/s^2\ \)
Resposta Questão 4
Alternativa B.
Iniciaremos calculando a aceleração desse corpo, através da fórmula da aceleração média:
\(a_m=\frac{∆v}{∆t}\)
\(a_m=\frac{v_f-v_i}{t_f-t_i}\)
\(a_m=\frac{0-10}{5-0}\)
\(a_m=-\frac{10}{5}\)
\(a_m=-2\ m/s^2\)
E finalizaremos calculando a distância final por meio da função horária da posição no MUV:
\(x_f=x_i+v_i\cdot t+\frac{a\cdot t^2}{2}\)
\(x_f=46+10\cdot8+\frac{-2\cdot8^2}{2}\)
\(x_f=46+80+\frac{-2\cdot64}{2}\)
\(x_f=46+80-64\)
\(x_f=62\ m\)
Resposta Questão 5
Alternativa E.
Calcularemos a aceleração do corpo através função horária da velocidade no MUV:
\(v_f=v_i+a\cdot t\)
\(40=0+a\cdot10\)
\(40=a\cdot10\)
\(a=\frac{40}{10}\)
\(a=4\ m/s^2\)
Resposta Questão 6
Alternativa A.
Distância, tempo, velocidade e aceleração são grandezas físicas estudadas na cinemática escalar, já a energia é uma grandeza física estudada na dinâmica.
Resposta Questão 7
Alternativa D.
Calcularemos a velocidade média por meio da sua fórmula:
\(v_m=\frac{∆x}{∆t}\)
\(v_m=\frac{x_f-x_i}{t_f-t_i}\)
\(v_m=\frac{200-40}{10-6}\)
\(v_m=\frac{160}{4}\)
\(v_m=40\ m/s\)
Resposta Questão 8
Alternativa C.
Iniciaremos transformando a aceleração do carro de km/h para m/s :
\(\frac{216\ km/h}{3,6}=60\ m/s\)
E finalizaremos calculando a aceleração através da fórmula que a relaciona a velocidade e ao tempo:
\(v_f=v_i+a\cdot t\)
\(60=0+a\cdot5\)
\(60=a\cdot5\)
\(a=\frac{60}{5}\)
\(a=12\ m/s^2\)
Resposta Questão 9
Alternativa E.
Calcularemos a variação de posição desse móvel através da equação de Torricelli:
\(v_f^2=v_i^2+2\cdot a\cdot∆x\)
\({50}^2=0^2+2\cdot2\cdot∆x\)
\(2500=0+4\cdot∆x\)
\(2500=4\cdot∆x\)
\(∆x=\frac{2500}{4}\)
\(∆x=625 m\)
Resposta Questão 10
Alternativa B.
Calcularemos o tempo através da função horária da posição no MUV:
\(x_f=x_i+v_i\cdot t+\frac{a\cdot t^2}{2}\)
\(x_f-x_i=v_i\cdot t+\frac{a\cdot t^2}{2}\)
\(\Delta x = v_i \cdot t + \frac{a \cdot t^2}{2} \)
\(2000=0\cdot+\frac{40\cdot t^2}{2}\)
\(2000=0+20\cdot t^2\)
\(2000=20\cdot t^2\)
\(t^2=\frac{2000}{20}\)
\(t^2=100\)
\(t=\sqrt{100}\)
\(t=10\ s\)
Resposta Questão 11
Alternativa D.
Calcularemos a velocidade inicial através da função horária da velocidade no MUV:
\(v_f=v_i+a\cdot t\)
\(25=v_i+3\cdot5\)
\(25=v_i+15\)
\(25-15=v_i\)
\(10\ m/s=v_i\)
Resposta Questão 12
Alternativa E.
I. A velocidade média é medida em metros por segundo. (correta)
II. O tempo é medido em segundos ao quadrado. (incorreta)
O tempo é medido em segundos.
III. O deslocamento inicial é medido em metros por segundo. (incorreta)
O deslocamento inicial é medido em metros.
IV. O deslocamento final é medido em metros. (correta)
