Questão 1
Veja a seguir a reação de cloração do etano na presença de luz:
![]()
Sabe-se que ela apresenta uma variação de entalpia igual a -35 Kcal.mol-1.Considerando os valores das energias de ligação presentes na reação, determine a energia da ligação C-Cl no composto CH3Cl.
C-H = 105 kcal.mol–1
Cl-Cl = 58 kcal.mol–1
H-Cl = 103 kcal.mol–1
C-C = 368 kcal.mol–1
a) -75 kcal.mol–1.
b) - 85 kcal.mol–1.
c) 85 kcal.mol–1.
d) - 95 kcal.mol–1.
e) 95 kcal.mol–1.
Questão 2
Observe a tabela referente aos valores de entalpias de ligação:
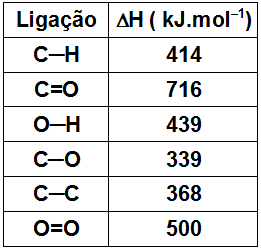
Com base nos valores fornecidos, qual será o valor do ΔH da combustão de 1 mol de metano?
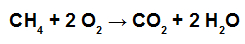
a) – 532 kJ.
b) – 632 kJ.
c) + 432 kJ.
d) + 332 kJ.
e) + 732 kJ.
Questão 3
(UNCISAL) No processo de Haber-Bosch, a amônia é obtida em alta temperatura e pressão, utilizando ferro como catalisador. Essa amônia tem vasta aplicação como fonte de nitrogênio na fabricação de fertilizante e como gás de refrigeração. Dadas as energias de ligação, H – H→ 436 kJ/mol, N≡ N→ 944 kJ/mol e H – N → 390 kJ/mol, a entalpia de formação de 1 mol de amônia é:
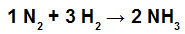
a) –88 kJ/mol.
b) –44 kJ/mol.
c) +44 kJ/mol.
d) +88 kJ/mol.
e) +600 kJ/mol.
Questão 4
(UniCESUMAR-SP) A ligação covalente que mantém os átomos de nitrogênio e oxigênio unidos no óxido nítrico, NO, não é explicada pela regra do octeto, mas a sua energia de ligação pode ser calculada a partir dos dados fornecidos abaixo. Dados:
Energia de ligação N≡N: 950 kJ.mol–1;
Energia de ligação O=O: 500 kJ.mol–1;
Entalpia de formação do NO: 90 kJ.mol–1.
A partir dessas informações, é possível concluir que a energia de ligação entre os átomos de nitrogênio e oxigênio no óxido nítrico é:
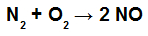
a) 90 kJ.mol–1.
b) 680 kJ.mol–1.
c) 765 kJ.mol–1.
d) 1360 kJ.mol–1.
e) 1530 kJ.mol–1.
Resposta Questão 1
Letra e).
Dados do exercício:
Ligação C–H: 105 kcal.mol–1
Ligação Cl–Cl: 58 kJ/mol
Ligação H-Cl = 103 kcal.mol–1
Ligação C-Cl = ?
Ligação C-C = 368 kcal.mol–1
ΔH = -35 Kcal.mol-1.
Inicialmente é importante reescrever a equação química, demonstrando todas as ligações existentes em cada molécula:
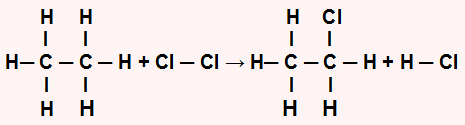
Em seguida, devemos determinar a quantidade de energia absorvida no reagente (Er) e liberada no produto (Ep) da reação:
Para o reagente: energia absorvida (sempre positiva, independentemente do sinal dos valores fornecidos). Nos reagentes, temos o etano com a ligação C-H seis vezes e com a ligação C-C uma vez, e o reagente Cl2 com a ligação Cl-Cl uma vez. Assim, temos:
Er = 6.EC-H + EC-C + 2.ECl-Cl
Er = 6.(105) + 368 + 58
Er = 630 + 368 + 58
Er = 1056 kcal.mol–1
Para o produto: energia liberada (sempre negativa, independentemente do sinal dos valores fornecidos). Nos produtos, temos 1 mol do cloroetano, que apresenta a ligação C-H cinco vezes, a ligação C-C uma vez e a ligação C-Cl uma vez, além de 1 mol do produto HCl, que apresenta a ligação H-Cl uma vez. Assim, temos:
Ep = 5.EC=H + EC-C + EC-Cl + EH-Cl
Ep = 5.(-105). + (-368) + (-x) + (-103)
Ep = - 525 - 368 - x -103
Ep = -996 - x kcal.mol–1
Com esses dados, utilizamos a expressão para o cálculo do ΔH envolvendo a energia de ligação:
ΔH = energia absorvida + energia liberada
-35 = 1056 + (-996 - x)
-35 = 1056 - 996 - x
x = 1056 - 996 +35
x = 1091 - 996
x = 95 kcal.mol–1
Resposta Questão 2
Letra a).
Dados do exercício:
Reagente CH4, C-H: 414 kJ.mol–1
Reagente O2, O=O: 500 kJ/mol
Produto CO2, C=O: 716 kJ/mol
Produto H2O, H– O: 439 kJ/mol
ΔH = ?
Inicialmente é importante reescrever a equação química, demonstrando todas as ligações existentes em cada molécula:
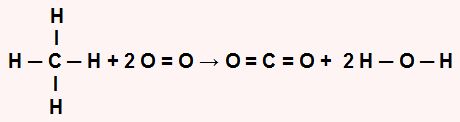
Em seguida, devemos determinar a quantidade de energia absorvida no reagente (Er) e liberada no produto (Ep) da reação:
Para o reagente: energia absorvida (sempre positiva, independentemente do sinal dos valores fornecidos). Nos reagentes, temos 1 mol do CH4, com a ligação C-H quatro vezes, e 2 mol de O2, no qual temos a ligação O=O. Assim, temos:
Er = 4.EC-H + 2.EO2
Er = 4.(414) + 2.(500)
Er = 1656 + 100
Er = 2656 kJ.mol–1
Para o produto: energia liberada (sempre negativa, independentemente do sinal dos valores fornecidos). Nos produtos, temos 1 mol de CO2, que possui duas ligações C=O, e 2 mol de água, que possui duas ligações H-O. Assim, temos:
Ep = 2.EC=O + 2.2.EH-O
Ep = 2.(-716). + 4(-439)
Ep = -1432 - 1756
Ep = -3188 kJ.mol–1
Com esses dados, basta utilizar a expressão para o cálculo do ΔH envolvendo a energia de ligação:
ΔH = energia absorvida + energia liberada
ΔH = 2656 + (-3188)
ΔH = - 532 kJ.mol–1
Resposta Questão 3
Letra b).
Dados do exercício:
Reagente N2, N≡N: 944 kJ.mol–1
Reagente H2, H – H: 436 kJ/mol
Produto NH3, H– N: 390 kJ/mol
ΔH = ?
Inicialmente é importante reescrever a equação química, demonstrando todas as ligações existentes em cada molécula:
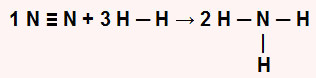
Em seguida, devemos determinar a quantidade de energia absorvida no reagente (Er) e liberada no produto (Ep) da reação:
Para o reagente: energia absorvida (sempre positiva, independentemente do sinal dos valores fornecidos). Nos reagentes, temos o N2 com a a ligação N≡N e 3 mol de H2 , que apresenta a ligação H-H. Assim, temos:
Er = 1.EN2 + 3. EH2
Er = 944 + 3.(436)
Er = 944 + 1308
Er = 2252 kJ.mol–1
Para o produto: energia liberada (sempre negativa, independentemente do sinal dos valores fornecidos). Nos produtos, temos 2 mol de NH3, que possui três ligações N-H. Assim, temos:
Ep = 2.3(- ENH3)
Ep = 6. (-390)
Ep = -2340 kJ.mol–1
Com esses dados, basta utilizar a expressão para o cálculo do ΔH envolvendo a energia de ligação:
ΔH = energia absorvida + energia liberada
ΔH = 2252 + (-2340)
ΔH = 2252 – 2340
ΔH = - 88 kJ.mol–1
Como o enunciado pede o valor do ΔH a cada mol de NH3 e o valor encontrado é referente a 2, temos:
ΔH =- 88
2
ΔH = -44 kJ.mol–1
Resposta Questão 4
Letra b).
Dados do exercício:
Reagente N2, N≡N: 950 kJ.mol–1
Reagente O2, O=O: 500 kJ.mol–1
Produto NO: x
ΔH = 90 kJ.mol–1
Inicialmente devemos determinar a quantidade de energia absorvida no reagente (Er) e liberada no produto (Ep) da reação:
Para o reagente: energia absorvida (sempre positiva, independentemente do sinal dos valores fornecidos). Nos reagentes, temos 1 mol do N2 com a ligação N≡N e 1 mol do O2 , que apresenta a ligação O=O. Assim, temos:
Er = EN2 + EO2
Er = 950 + 500
Er = 1450 kJ.mol–1
Para o produto: energia liberada (sempre negativa, independentemente do sinal dos valores fornecidos).
Ep = 2.(- ENO)
Ep = - 2.x
Com esses dados, basta utilizar a expressão para o cálculo do ΔH envolvendo a energia de ligação:
ΔH = energia absorvida + energia liberada
90 = 1450 + (-2x)
90 = 1450 - 2x
2x = 1450 – 90
2x = 1360
x = 1360
2
x = 680 kJ.mol–1.



