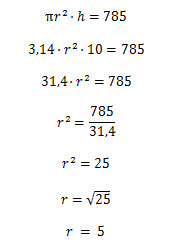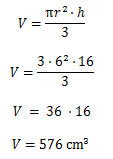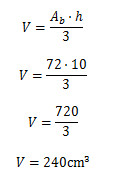Questão 1
Uma piscina está com 75% da sua capacidade cheia. Sabendo que ela possui o formato de um paralelepípedo retângulo, com 1,5 metros de profundidade, 6 metros de largura e 5 metros de comprimento, o volume que falta para encher toda a piscina, em litros, é de:
A) 11 250 litros
B) 22 500 litros
C) 33 750 litros
D) 45 000 litros
E) 90 000 litros
Questão 2
A soma do comprimento das arestas de um cubo é igual a 48 cm, então o volume desse cubo é de:
A) 125 cm³
B) 64 cm³
C) 32 cm³
D) 27 cm³
E) 21 cm³
Questão 3
Uma bola de basquete possui o diâmetro de 24 cm. Utilizando 3,1 como aproximação para \(π, \) o volume dessa bola é de
A) 1232 cm³
B) 2380 cm³
C) 7142 cm³
D) 54139 cm³
E) 71412 cm ³
Questão 4
Um objeto possui formato de um prisma de base hexagonal, como o da imagem a seguir:
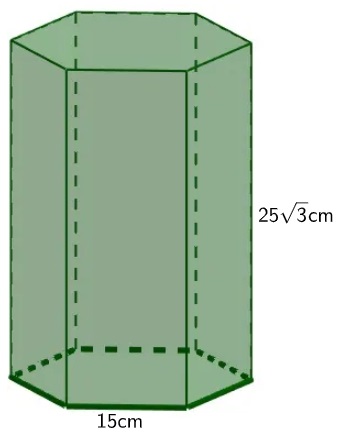
Analisando esse objeto, podemos afirmar que o seu volume é igual a:
A) 12310,5 cm³
B) 18312,5 cm³
C) 22320,0 cm³
D) 25312,5 cm³
E) 50624,0 cm³
Questão 5
Um reservatório possui formato de um cilindro e está com 60% da sua capacidade ocupada. Sabendo que ele possui raio igual a 2 m e altura de 10 m, o volume que ainda cabe nesse reservatório, em litros, é igual a:
(Use \(π\) = 3)
A) 120 000
B) 72 000
C) 64 000
D) 48 000
E) 12 000
Questão 6
Um cilindro possui 10 cm de altura e volume igual a 785 cm³. Nessas condições, podemos afirmar que o raio desse cilindro é igual a:
(Use \(π \) = 3,14)
A) 4 cm
B) 5 cm
C) 6 cm
D) 7 cm
E) 8 cm
Questão 7
A embalagem de um produto possui o formato de um cone. O diâmetro da base desse cone é de 12 cm, sua altura é de 16 cm, e o seu volume está totalmente preenchido. O volume que vem em cada unidade desse produto é de:
(Use π = 3)
A) 237 cm³
B) 352 cm³
C) 394 cm³
D) 420 cm³
E) 576 cm³
Questão 8
Um reservatório de grãos em uma fazenda tem 6 metros de altura e o formato de uma pirâmide cuja base é um triângulo equilátero de lados medindo 4 metros. Qual é o volume desse reservatório em metros cúbicos?
A)\(4√3\)
B) \(6√3\)
C) \(8√3\)
D) 12
E) \(10√2\)
Questão 9
Uma pirâmide reta possui como base um quadrado cujo lado mede \(6√2c\)cm. Se a sua altura é 10 cm, então o seu volume, em cm³, é de:
A) 240
B) 340
C) 480
D) 500
E) 720
Questão 10
Um cone possui 12 cm de diâmetro e 12 cm de altura. Diante disso, sua capacidade volumétrica é de:
A) \( 36π\)
B) \(144π\)
C) \(288π\)
D) \(576π\)
Questão 11
(Enem 2010) Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que é interno, mede 8 cm.
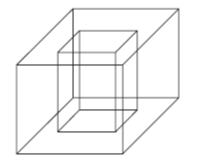
O volume de madeira utilizado na confecção desse objeto foi de
A) 12 cm³
B) 64 cm³
C) 96 cm³
D) 1216 cm³
E) 1728 cm³
Questão 12
(UEG-GO 2015) Suponha que haja laranjas no formato de uma esfera com 6 cm de diâmetro e que a quantidade de suco que se obtém ao espremer cada laranja é 2/3 de seu volume, sendo o volume dado em litros. Nessas condições, se quiser obter 1 litro de suco de laranja, deve-se espremer no mínimo:
(Use π = 3,14)
A) 13 laranjas
B) 14 laranjas
C) 15 laranjas
D) 16 laranjas
Resposta Questão 1
Alternativa A
Para calcular o volume total do sólido geométrico em questão, multiplicaremos suas três dimensões:
\(V = 1,5 ⋅6 ⋅5\)
\(V = 1,5 ⋅30 \)
\(V=45 m^3\)
Transformamos isso em litros ao multiplicar por 1000:
\(V= 45 ⋅1000 \)
\(V = 45 000 litros\)
Esse é o volume total da piscina. Se que 75% dela está ocupada, 25% está vazia. Sendo assim, temos:
\(45 000 ⋅0,25 = 11 250 litros\)
Resposta Questão 2
Alternativa B
Um cubo possui 12 arestas. Ao dividir 48 por 12, encontraremos o comprimento de cada aresta:
\(a = 48∶ 12 = 4 \)
Se cada aresta mede 4 cm, o volume do cubo em questão é igual a:
\(V=a^3\)
\(V=4^3\)
\(V = 64 cm³\)
Resposta Questão 3
Alternativa C
Se o diâmetro é de 24 cm, então o raio será a sua metade, ou seja, r = 12 cm.
Calculando o volume de uma esfera, temos:
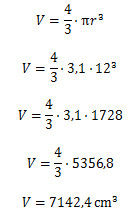
Arredondando, obtemos:
\(V≈7142cm^3\)
Resposta Questão 4
Alternativa D
O volume de um prisma é o produto entre a área da base e sua altura. Como a base é um hexágono regular, temos:
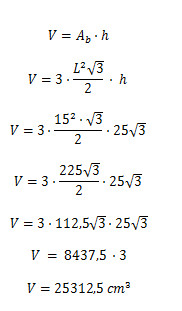
Resposta Questão 5
Alternativa D
Primeiramente, calcularemos o volume total de um cilindro, o sólido geométrico da estrutura do reservatório:
\(V=πr^2⋅h\)
\(V=3⋅2^2⋅10\)
\( V = 3 ⋅4 ⋅10 \)
\(V=120m^3\)
Considerando que 60% estão cheios, restam 40%. Calculando, temos:
\(0,4 ⋅120 = 48 m³\)
Por fim, transformando para litros, uma vez que a unidade de medida da questão não é metro cúbico, temos:
\(48 ⋅1000 = 48 000 litros\)
Resposta Questão 7
Resposta Questão 8
Alternativa C
O volume da pirâmide é calculado por:
![]()
Como a base é um triângulo equilátero de lado 4, temos:
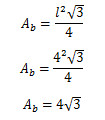
Logo, obtemos o seguinte:
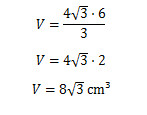
Resposta Questão 9
Resposta Questão 10
Alternativa B
Como o diâmetro do cone é 12 cm, então o raio é a metade. Logo, r = 6 cm. Também sabemos que a sua altura é 12 cm. Logo, h = 12 cm.
Calculando o volume, substituindo os valores conhecidos na fórmula, temos que:
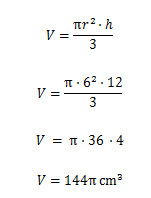
Resposta Questão 11
Alternativa D
Para encontrar o volume do porta-lápis, calcularemos a diferença entre o volume do cubo maior e o volume do cubo menor.
12³ – 8³ = 1728 – 512 = 1216 cm³
Resposta Questão 12
Alternativa B
Sabemos que
1 litro = 1 dm³,
então, calcularemos o volume da laranja utilizando o raio em dm.
- Diâmetro: 6 cm = 0,6 dm
- Raio: 0,6 : 2 = 0,3 dm
Calcularemos 23 do volume da laranja. Assim, temos:
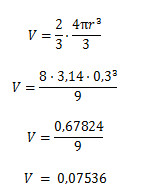
Se cada laranja produz 0,07536 litros, 1 : 0,07536 = 13,27 laranjas. Como é impossível haver 0,27 laranjas, arredondaremos o total para 14 laranjas.