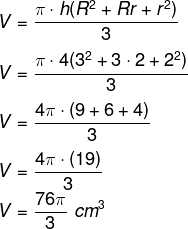Questão 1
Analise a planificação do sólido geométrico a seguir:
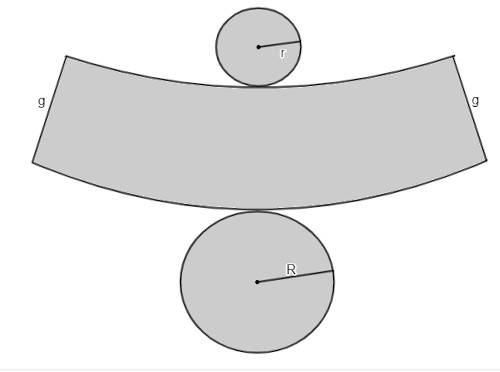
A classificação de sólido geométrico a que essa planificação pertence é de
A) cilindro.
B) prisma.
C) esfera.
D) tronco de cone.
E) cone.
Questão 2
Um contêiner foi construído no formato de um tronco de cone reto, com raio maior de 4 m, raio menor de 1 m e altura de 4 m. Para a conservação do contêiner, foi contratado um pintor que cobra R$ 2,00 por m² para pintar a área externa. Diante dessa situação, qual será o valor gasto para pintar todo o contêiner? (Use π = 3,1).
A) R$ 251,10.
B) R$ 120,60.
C) R$ 175,00.
D) R$ 260,40.
E) R$ 130,20.
Questão 3
O volume de um copo em formato de tronco de cone, com raios das bases medindo 4 cm e 6 cm e altura medindo 9 cm, é de (em centímetros cúbicos):
A) 144π.
B) 145π.
C) 168π.
D) 210π.
E) 228π.
Questão 4
Um tronco de cone possui raio da base maior igual a 24 cm e raio da base menor igual a 16 cm. Sabendo que sua altura é igual a 6 cm, podemos afirmar que a medida de sua geratriz é igual a
A) 8 cm.
B) 10 cm.
C) 12 cm.
D) 15 cm.
E) 18 cm.
Questão 5
Sobre o tronco de cone, julgue as afirmativas as seguir:
I → É um caso particular de cilindro.
II → É um sólido geométrico.
III → É um poliedro.
Marque a alternativa correta.
A) Somente I é verdadeira.
B) Somente II é verdadeira.
C) Somente III é verdadeira.
D) Todas as afirmativas são falsas.
Questão 6
Um porta-joias é feito no formato de um tronco de cone com altura igual a 12 cm, raio da base maior igual a 10 cm e raio da base menor igual a 5 cm. Use π = 3 e determine: qual a área total desse porta-joias?
A) 970 cm².
B) 960 cm².
C) 950 cm².
D) 940 cm².
E) 920 cm².
Questão 7
(UFMS) Em uma padaria são produzidos bombons em formato de tronco de cone, conforme a figura a seguir:
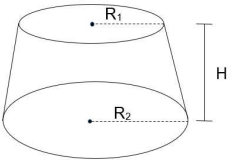
Considerando R1 = 2 cm, R2 = 3 cm e H = 4 cm, qual o volume de cada bombom em cm³?
A) 100π/3.
B) 52π/3.
C) 76π/3.
D) 65π/3.
E) 95π/3.
Questão 8
Um determinado tronco de cone possui geratriz igual a 5 cm, raio maior igual a 7 cm e raio menor igual a 4 cm. O volume desse tronco de cone é igual a: (use π = 3)
A) 372 cm³.
B) 395 cm³.
C) 402 cm³.
D) 453 cm³.
E) 505 cm³.
Questão 9
Em uma fazenda, há um depósito para soja que possui o formato de um tronco de cone, sendo que o raio da base maior mede 10 m e o raio da base menor tem 7 m de comprimento. Qual é a capacidade desse depósito, em metros cúbicos, sabendo que ele possui 6 m de altura?
A) 218π.
B) 325π.
C) 349π.
D) 438π.
E) 938π.
Questão 10
A professora Kamila desafiou os seus estudantes a investigarem as formas geométricas que estavam à sua volta. O estudante Pedro identificou a maioria das formas corretamente, exceto as duas a seguir:
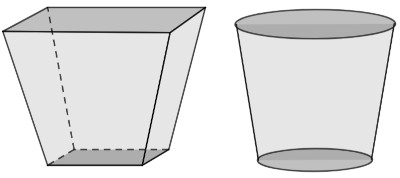
Analisando essas formas geométricas, podemos afirmar que elas são, respectivamente,
A) um trapézio e um cilindro.
B) um tronco de prisma e um cone.
C) um prisma e um tronco de cilindro
D) um tronco de pirâmide e um tronco de cone
E) um cubo e um prisma de base circular.
Questão 11
(Nucepe) Como é e para que serve prioritariamente uma xícara todos sabemos: servir bebidas, especialmente quentes. Mas de onde surgiu a ideia de criar um “copo com alça”?
O chá, que tem origem oriental, era inicialmente servido em potes redondos, sem alças. Segundo a tradição, isso era até mesmo um alerta para quem conduzia a cerimônia da bebida: caso o recipiente queimasse as pontas dos dedos, estava quente demais para ser ingerido. Na temperatura ideal, ela não incomodava, mesmo com o contato direto com a porcelana.
Fonte: http://www.mexidodeideias.com.br/viagem/a-historia-da-xicara. Acesso em 06/01/2018.
Uma xícara de chá tem a forma de um tronco de cone reto, conforme a figura abaixo. Qual o volume máximo, aproximado, de líquido que ela pode conter?
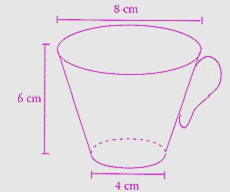
A) 168 cm³.
B) 172 cm³.
C) 166 cm³.
D) 176 cm³.
E) 164 cm³.
Questão 12
(Enem 2013) Uma cozinheira, especialista em fazer bolos, utiliza uma forma no formato representado na figura:
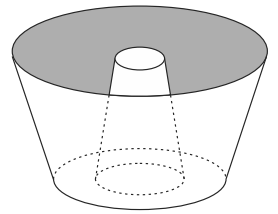
Nela identifica-se a representação de duas figuras geométricas tridimensionais. Essas figuras são
A) um tronco de cone e um cilindro.
B) um cone e um cilindro.
C) um tronco de pirâmide e um cilindro.
D) dois troncos de cone.
E) dois cilindros.
Resposta Questão 1
Alternativa D
Essa é a planificação de um tronco de cone. Note que ela possui duas bases formadas por círculos semelhantes.
Resposta Questão 2
Alternativa D
Para calcular a área total do contêiner, primeiramente encontraremos sua geratriz:
g² = h² + (R – r)²
g² = 4² + (4 – 1)²
g² = 16 + 3²
g² = 16 + 9
g² = 25
g = √25
g = 5 m
Calculando a área da base maior:
AB = πR²
AB = 3,1 · 4²
AB = 3,1 · 16
AB = 49,6 m²
Agora, calculando a área da base menor:
Ab = πr²
Ab = 3,1 · 1²
Ab = 3,1 m²
Determinando a área lateral:
Al = πg (R + r)
Al = 3,1 · 5 (4 + 1)
Al = 15,5 · 5
Al = 77,5 m²
Portanto, a área total é de:
AT = 49,6 + 3,1 + 77,5 = 130,2 m²
Como o valor cobrado é de R$ 2,00 por m², basta multiplicar a área total por 2:
130,2 · 2 = 260,4
O valor pago será de R$ 260,40.
Resposta Questão 3
Alternativa E
Para descobrir o volume do tronco de cone, tem-se o seguinte:
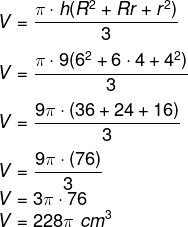
Resposta Questão 4
Alternativa B
Sabemos que:
g² = h² + (R – r)²
Substituindo os valores conhecidos, temos o seguinte cálculo:
g² = 6² + (24 – 16)²
g² = 36 + 8²
g² = 36 + 64
g² = 100
g = √100
g = 10 cm
Resposta Questão 5
Alternativa B
-
I → Falsa, pois o tronco de cone não pode ser considerado um cilindro, já que este possui duas bases congruentes, o que não acontece com aquele.
-
II → Verdadeira, pois o tronco de cone é de fato classificado como sólido geométrico.
-
III → Falsa, pois o tronco de cone não é um poliedro, já que ele possui faces formadas por círculos, e não por polígonos.
Resposta Questão 6
Alternativa B
De início, encontraremos a geratriz para podermos calcular a área lateral:
g² = 12² + (10 – 5)²
g² = 12² + 5²
g² = 144 + 25
g² = 169
g = √169
g = 13
Al = πg (R + r)
Al = 3 · 13 (10 + 5)
Al = 39 · 15
Al = 585 cm²
Agora, calcularemos a área de cada uma das bases:
AB = πR²
AB = 3 · 10²
AB = 3 · 100
AB = 300 cm²
Ab = πr²
Ab = 3 · 5²
Ab = 3 · 25
Ab = 75 cm²
AT = AB + Ab + Al
AT = 300 + 75 + 585 = 960 cm²
Resposta Questão 8
Alternativa A
Lembrando da fórmula g² = h² + (R – r)², calcularemos:
5² = h² + (7 – 4)²
5² = h² + 3²
25 = h² + 9
25 – 9 = h²
h² = 16
h = √16
h = 4
Conhecendo a altura do tronco, calcularemos o seu volume:
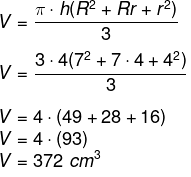
Resposta Questão 9
Alternativa D
Para calcular o volume, temos os seguintes valores:
h = 6 m
R = 10 m
r = 7 m
Aplicando a fórmula do volume, obtemos:
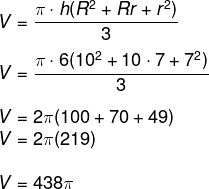
Resposta Questão 10
Alternativa D
Ao analisar as imagens, percebemos que há dois sólidos que são respectivamente um tronco de pirâmide e um tronco de cone.
Resposta Questão 11
Alternativa D
Para encontrar o volume, primeiro encontraremos o valor de cada um dos raios. Para isso, basta dividir o diâmetro por dois.
R = 8/2 = 4
r = 4/2 = 2
Além do raio, sabemos que h = 6. Portanto, podemos fazer o seguinte cálculo:
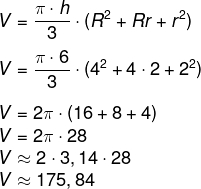
O valor mais próximo é de 176 cm³.
Resposta Questão 12
Alternativa D
Quando analisamos a imagem, é possível perceber que no centro da forma há um tronco de cone. Além disso, se analisarmos a forma integralmente, percebemos que ela também possui o formato de um tronco de cone. Então, há na imagem dois troncos de cone.