Questão 1
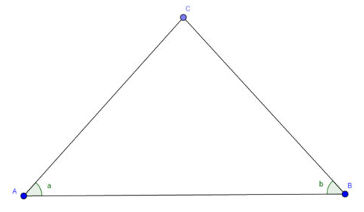
Considere o triângulo ABC, onde os ângulos a e b são iguais. Mostre que esse triângulo é isósceles.
Questão 3
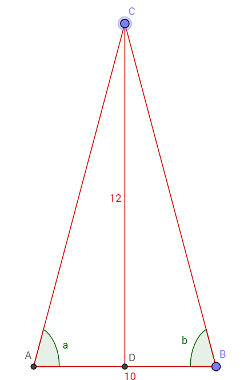
Em um triângulo isósceles, ABC foi desenhada com altura relativa à base AB medindo 12 cm. Sabendo que a medida da base do triângulo é 10 cm, determine os lados CB e CA desse triângulo.
Questão 4
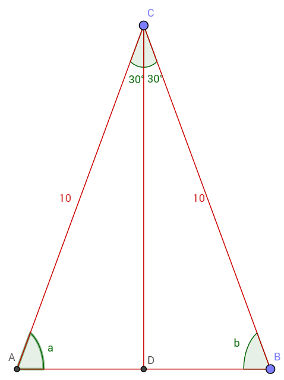
Um triângulo ABC possui lados CB = 10 cm e AB = 10 cm. Além disso, foi desenhado um segmento de reta partindo do vértice C até a base AB dividindo o ângulo interno do vértice C em dois ângulos iguais de 30 graus. Calcule o valor dos ângulos a e b, internos ao triângulo e localizados nos vértices A e B respectivamente.
Resposta Questão 1
Sabendo que os ângulos a e b são iguais, podemos considerá-los como ângulos da base, sendo assim, a base desse triângulo é o lado AB. Para mostrar que ABC é isósceles, devemos mostrar que os lados AC e BC são iguais.
Para tanto, basta construir a altura CD relativa à base BC.
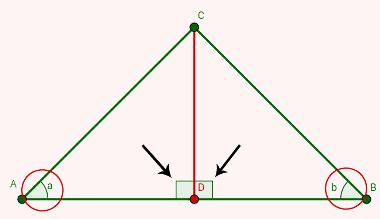
Essa altura parte do vértice C e encontra a base AB, formando com ela ângulos de 90 graus. Essa altura divide o triângulo inicial em outros dois triângulos, CBD e ACD.
Agora, basta observar que o lado CD é comum aos dois triângulos, os ângulos “a” e “b” são iguais, assim como os ângulos de 90 graus provenientes da construção da altura. Isso configura o caso LAAo de congruência de triângulos, dessa forma, os lados correspondentes AC e BC são também congruentes. Portanto, o triângulo ABC é isósceles.
Resposta Questão 2
Triângulos equiláteros são aqueles que possuem 3 lados iguais. Uma consequência disso é que os três ângulos do triângulo equilátero também são iguais.
Primeiramente, construa a mediana do triângulo equilátero, que o divide nos triângulos ACD e BCD.
Uma vez feito isso, o lado AB do triângulo equilátero deve ser dividido em duas partes iguais: AD e DB
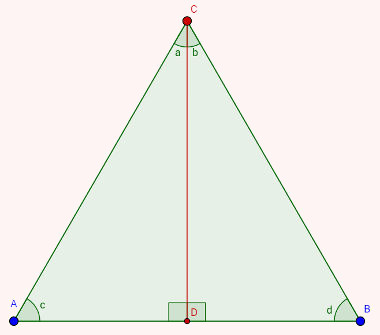
Observe que:
i- Os lados CB e AC são iguais, pois o triângulo é equilátero
ii- O lado CD é comum aos dois triângulos ACD e BCD
iii- Os lados AD e DB são congruentes por serem resultado da construção da mediana do triângulo equilátero.
Essas informações configuram o caso LLL de congruência de triângulos. Portanto, os triângulos ACD e BCD são congruentes.
Conclusões provenientes da congruência entre os triângulos ACD e BCD:
a) Os ângulos “a” e “b” são iguais, portanto CD é bissetriz;
b) Os segmentos AD e BD são iguais, o que implica que CD também é mediana.
Resposta Questão 3
Como se trata de um triângulo isósceles, podemos afirmar:
CA = CB, a = b e altura, mediana e bissetriz são o mesmo segmento.
Pode-se concluir, então, que os segmentos AD e DB são congruentes, já que CD é mediana. Logo, DB = 5 cm.
Utilizando o teorema de Pitágoras, teremos:
5² + 12² = x²
25 + 144 = x²
169 = x²
x = √169
x = 13 cm.
Lembrando que x = CB e que CB é hipotenusa, pois CD é altura e assim descreve um ângulo de 90 graus.
CB portanto é 13 cm, que é a mesma medida de CA, pois o triângulo é isósceles.
Resposta Questão 4
Note que os lados CB e AB desse triângulo são iguais, portanto ele é isósceles. Sabendo que os ângulos da base de um triângulo isósceles são iguais, a = b. Note também que o segmento CD é bissetriz desse triângulo, portanto é também altura. Dessa forma, o ângulo que o segmento CD forma com a base AB é de 90 graus. Ora, a soma dos ângulos internos de um triângulo é de 180 graus. Então, podemos descobrir o valor do ângulo a com a seguinte soma:
a + 30 + 90 = 180
a = 180 – 90 – 30
a = 60
Como a = b, então b também é 60 graus.



