Questão 1
O triângulo retângulo, a seguir, possui perímetro igual a 48 cm, então, o valor de x é igual a:
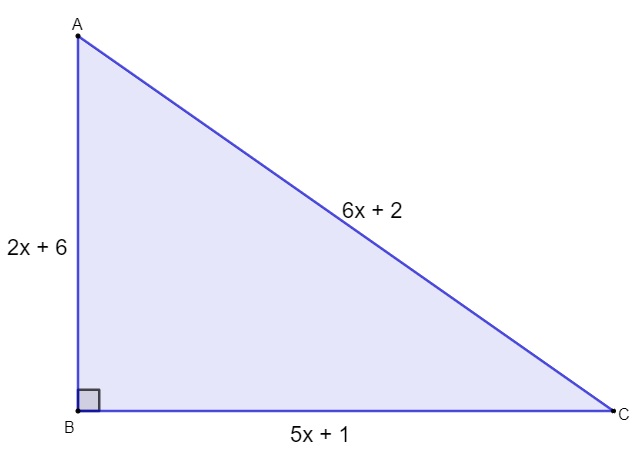
A) 2
B) 3
C) 4
D) 5
E) 6
Questão 2
Em um triângulo retângulo, os seus outros dois ângulos internos medem 2x + 5 e x + 10. Sabendo disso, podemos afirmar que o valor do menor ângulo desse triângulo retângulo é:
A) 25º
B) 35º
C) 50º
D) 55º
E) 60º
Questão 3
Uma fazenda possui formato retangular. Durante a compra, um agricultor viu que, pela legislação vigente, ele não poderá desmatar metade desse terreno, sendo assim, ele o dividiu diagonalmente conforme a imagem a seguir:
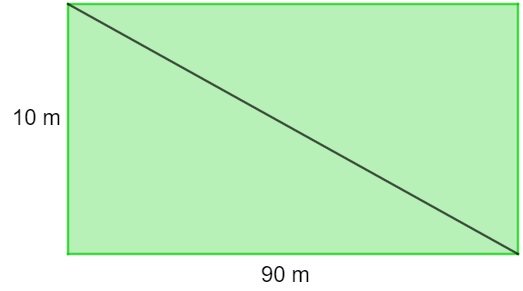
A área que deve ser mantida preservada é de:
A) 100 m²
B) 350 m²
C) 200 m²
D) 900 m²
E) 450 m²
Questão 4
Sobre o triângulo retângulo, julgue as afirmativas a seguir:
I → Um triângulo retângulo pode ser também isósceles.
II → Um triângulo retângulo pode ser equilátero.
III → Um triângulo retângulo pode ser escaleno.
Marque a alternativa correta:
A) Somente a I é verdadeira.
B) Somente a II é verdadeira.
C) Somente a III é verdadeira.
D) Somente I e II são verdadeiras.
E) Somente I e III são verdadeiras.
Questão 5
(Instituto Excelência) De acordo com a definição básica do teorema de Pitágoras, assinale a alternativa CORRETA:
A) O teorema de Pitágoras relaciona as medidas dos catetos de um triângulo retângulo à medida de sua hipotenusa. O teorema de Pitágoras diz que: “a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”.
B) O teorema de Pitágoras pode ser determinado pela seguinte lei de correspondência: “Feixes de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes”.
C) O teorema de Pitágoras pode ser utilizado para fazer a divisão de polinômios. Para fazer a divisão de um polinômio P(x) por outro polinômio Q(x), é fundamental que o polinômio Q(x) seja da forma x + u ou x – u, isto é, deve ser um binômio de 1° grau.
D) Nenhuma das alternativas.
Questão 6
Um parque possui o formato de um triângulo retângulo conforme a imagem a seguir:
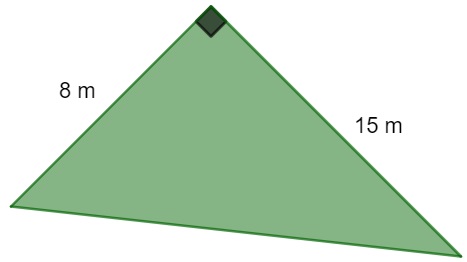
Se uma pessoa completar 250 voltas em torno desse parque, ela andou um total de:
A) 5000 metros
B) 10.000 metros
C) 12.500 metros
D) 15.000 metros
E) 17.500 metros
Questão 7
(UFPI - Adaptada) Um avião decola, percorrendo uma trajetória retilínea, formando com o solo um ângulo de 30° (suponha que a região sobrevoada pelo avião seja plana). Depois de percorrer 1000 metros, a altura atingida pelo avião, em metros, é:
A) 200 metros
B) 300 metros
C) 400 metros
D) 500 metros
E) 600 metros
Questão 8
Uma pessoa avistou um prédio estando no ponto A, com uma distância de 16 metros, conforme a imagem a seguir:
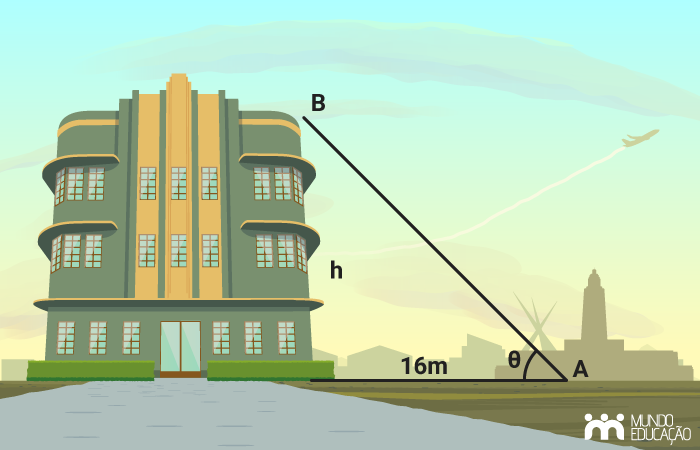
Sabendo que o ângulo θ mede 45º, então, podemos afirmar que a altura h do prédio é de:
A) 12 metros
B) 16 metros
C) 20 metros
D) 22 metros
E) 25 metros
Questão 9
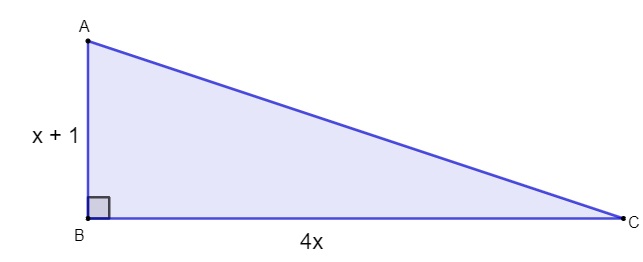
A área do triângulo retângulo a seguir é de 60 cm². Sabendo disso, podemos afirmar que a soma dos seus catetos é igual a:
A) 22 cm
B) 23 cm
C) 25 cm
D) 26 cm
E) 28 cm
Questão 10
(IFG 2020) O desmatamento tem sido uma problemática crescente no Brasil. Supondo que, ao efetuar o desmatamento de uma determinada área, um madeireiro se depara com uma árvore que já se encontra quebrada; parte do tronco da árvore que se manteve fixa ao solo mede 3 m e forma com este um ângulo de 90⁰; a ponta da parte quebrada que toca o solo encontra-se a 4 m de distância da base da árvore. Qual era a altura da árvore antes de se quebrar:
A) 5 m
B) 7 m
C) 8 m
D) 9 m
Questão 11
Analise o triângulo e julgue as afirmativas a seguir:
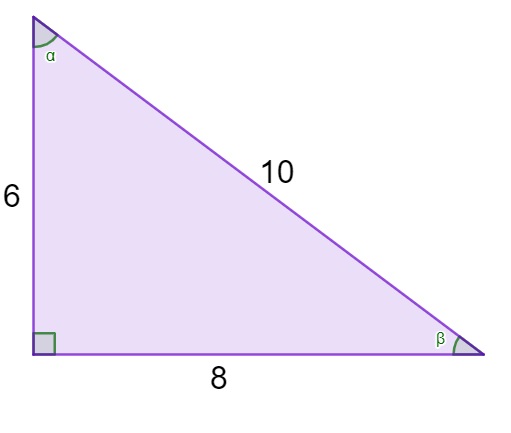
I → O triângulo é um triângulo retângulo.
II → A tangente do ângulo ꞵ é igual a 0,75.
III → O cosseno de α é igual a 0,6.
Podemos afirmar que:
A) Somente a afirmativa I está incorreta.
B) Somente a afirmativa II está incorreta.
C) Somente a afirmativa III está incorreta.
D) Todas as afirmativas estão incorretas.
E) Todas as afirmativas estão corretas.
Questão 12
(Enem) Um balão atmosférico, lançado em Bauru (343 quilômetros a noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de medição.
Disponível em: http://www.correiodobrasil.com.br. Acesso em: 02 maio 2010.
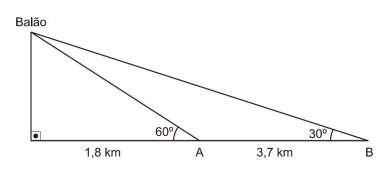
Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°. Qual a altura aproximada em que se encontrava o balão?
A) 1,8 km
B) 1,9 km
C) 3,1 km
D) 3,7 km
E) 5,5 km
Resposta Questão 1
Alternativa B
Sabemos que o perímetro de um triângulo é igual à soma dos seus lados, então, temos que:
P = 5x + 1 + 6x + 2 + 2x + 6
P = 13x + 9
Contudo, temos a informação de que o perímetro é 48 cm, então, temos que:
13x + 9 = 48
13x = 48 – 9
13x = 39
x = 39 : 13
x = 3
Resposta Questão 2
Resposta Questão 3
Alternativa E
Estamos calculando a área de um triângulo retângulo de base igual a 90 metros e altura igual a 10 metros, então, temos que:
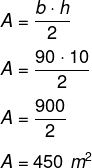
Resposta Questão 4
Alternativa E
I → Um triângulo retângulo pode ser também isósceles. (verdadeira)
Se um ângulo for 90º e os demais 45º cada um, teremos um triângulo retângulo que é isósceles.
II → Um triângulo retângulo pode ser equilátero. (falsa)
O triângulo equilátero possui os ângulos internos iguais a 60º, logo, é impossível que exista um triângulo retângulo que seja equilátero.
III → Um triângulo retângulo pode ser escaleno. (verdadeira)
Um triângulo retângulo pode ter os três lados com medidas distintas, o que é bastante comum.
Resposta Questão 5
Alternativa A
A alternativa que descreve corretamente o teorema de Pitágoras é a A.
Resposta Questão 6
Alternativa B
Primeiro chamaremos de x o lado desconhecido do parque, ele é a hipotenusa do triângulo, então, pelo teorema de Pitágoras, temos que:
x² = 8² + 15²
x² = 64 + 225
x² = 289
x = √289
x = 17
Assim, uma volta completa é igual ao perímetro:
P = 8 + 15 + 17
P = 40
Portanto, 250 voltas resultarão em 250 · 40 = 10.000 metros.
Resposta Questão 7
Alternativa D
Nesse caso aplicaremos a trigonometria. Primeiro faremos a imagem que representa essa situação:
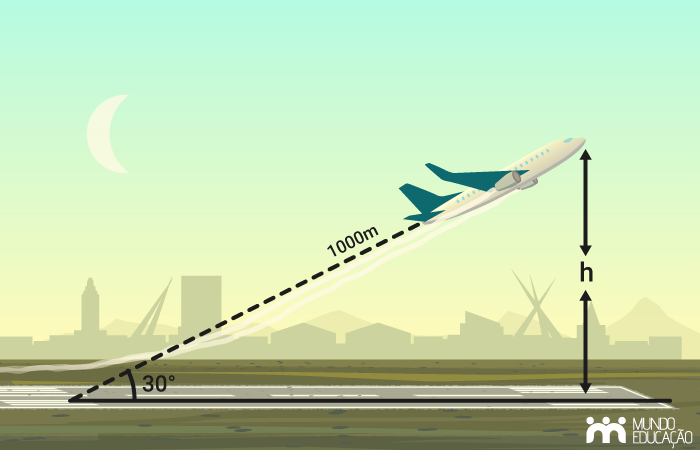
Como esse triângulo é retângulo, podemos aplicar o seno de 30º para encontrar o valor da altura:
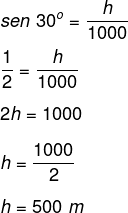
Resposta Questão 8
Alternativa B
Sabendo que o ângulo mede 45º e o outro, 90º, sendo x o valor do terceiro ângulo, temos que:
x + 45 + 90 = 180
x + 135 = 180
x = 180 – 135
x = 45º
Como x também mede 45º, esse triângulo é isósceles, ou seja, possui dois lados congruentes, sabendo disso, então, h = 16 metros.
Resposta Questão 9
Alternativa D
Se a área é de 60 metros, então:
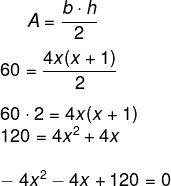
Encontramos uma equação do segundo grau, então, calcularemos o valor das suas soluções calculando o delta e aplicando a fórmula de Bhaskara. Primeiro calcularemos o delta.
a = -4, b = -4 e c = 120
Δ = b² – 4ac
Δ = (-4) ² – 4 · (-4) · 120
Δ = 16 + 1920
Δ = 1936
Agora, aplicando a fórmula de Bhaskara:
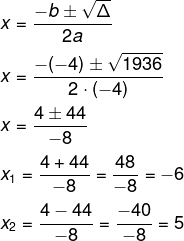
A solução -6 não faz sentido por ser negativa, pois não é possível a medida de um lado ser negativa, então, resta-nos que x = 5.
Assim, os catetos medem:
x + 1 = 5 + 1 = 6
4x = 4 · 5 = 20
A soma entre eles é 20 + 6 = 26.
Resposta Questão 10
Alternativa C
Analisando as informações dadas, vamos construir a imagem que representa essa situação:
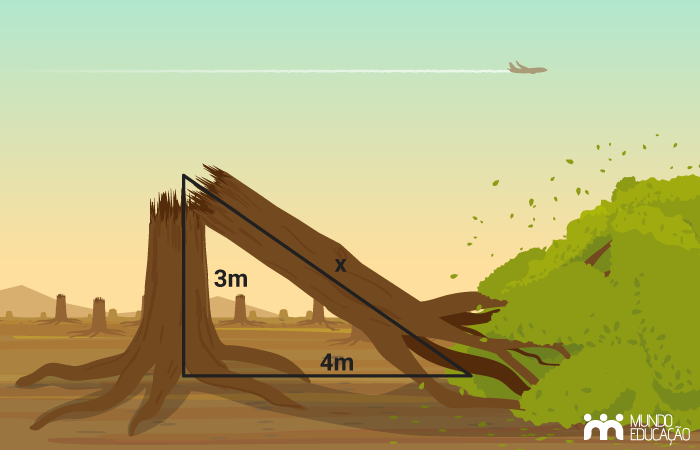
A altura da árvore é dada pela soma de 3 + x. Para encontrar o valor de x, aplicamos o teorema de Pitágoras.
x² = 3² + 4²
x² = 9 + 16
x² = 25
x = √25
x = 5
Então, a altura será 3 + 5 = 8 metros.
Resposta Questão 11
Alternativa E
I → O triângulo é um triângulo retângulo. (verdadeira)
Note que ele possui um ângulo de 90º, logo, ele é retângulo.
II → A tangente do ângulo ꞵ é igual a 0,75. (verdadeira)
A tangente de ꞵ é a divisão entre o cateto oposto ao ângulo, que mede 6, e o cateto adjacente ao ângulo, que mede 8, ou seja, 6 : 8 = 0,75.
III → O cosseno de α é igual a 0,6. (verdadeira)
O cosseno do ângulo α é igual ao cateto adjacente a ele, que mede 6, divido pela hipotenusa do triângulo, que mede 10, ou seja, 6 : 10 = 0,6.
Resposta Questão 12
Alternativa C
Analisando a imagem, podemos perceber que a altura h pode ser dada pela tangente de 60º:
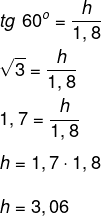
Então, a altura é de aproximadamente 3,1 km.



