Questão 1
Um triângulo escaleno possui perímetro igual a 36 cm. Se os seus lados medem respectivamente x + 2, 2x – 5 e x – 1, o valor do maior lado desse triângulo é:
A) 18 cm
B) 15 cm
C) 12 cm
D) 10 cm
E) 9 cm
Questão 2
Um triângulo é conhecido como escaleno quando:
A) ele possui um ângulo de 90°.
B) ele possui todos os ângulos agudos.
C) as medidas dos lados são congruentes.
D) as medidas de dois lados são congruentes.
E) as medidas dos lados são todas distintas.
Questão 3
Analise o triângulo a seguir:
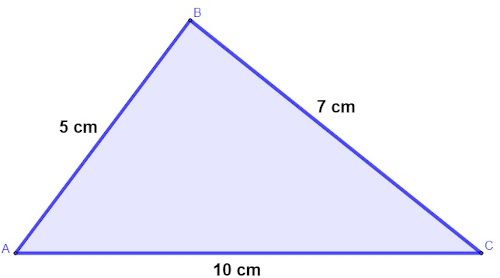
Esse triângulo pode ser classificado como:
A) triângulo retângulo.
B) triângulo equilátero.
C) triângulo isósceles.
D) triângulo obtusângulo.
E) triângulo escaleno.
Questão 4
Um triângulo escaleno possui lados medindo 6 cm, 10 cm e 8 cm. A área desse triângulo é igual a:
A) 12 cm²
B) 16 cm²
C) 24 cm²
D) 36 cm²
E) 40 cm²
Questão 5
Sobre o triângulo escaleno, podemos afirmar que ele pode ser também:
I – obtusângulo.
II – retângulo.
III – acutângulo.
Marque a alternativa correta:
A) Somente I é falsa
B) Somente II é falsa
C) Somente III é falsa
D) Todas são verdadeiras.
Questão 6
Um terreno no formato de um triângulo escaleno possui área igual a 24 cm². Se o seu lado mede x e a sua altura mede x + 2, podemos afirmar que a altura desse triângulo é igual a:
A) 8 cm
B) 6 cm
C) 5 cm
D) 4 cm
E) 3 cm
Questão 7
Dado o triângulo escaleno a seguir:
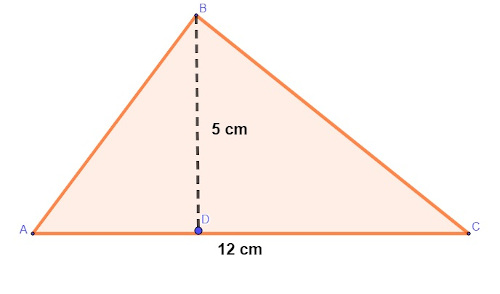
A área do triângulo escaleno é igual a:
A) 30 cm²
B) 45 cm²
C) 60 cm²
D) 75 cm²
E) 120 cm²
Questão 8
Um triângulo escaleno possui perímetro igual a 43 cm. Sabendo que um dos seus lados mede 16 cm e o outro mede 14 cm, a medida do terceiro lado é:
A) 8 cm
B) 9 cm
C) 10 cm
D) 13 cm
E) 15 cm
Questão 9
(Fundatec) Um triângulo que tem base b e altura h sofreu algumas alterações. Sua base cresceu 30%, e sua altura diminuiu 20%. Sendo assim, é correto afirmar que sua área:
A) se manteve a mesma.
B) diminuiu 4%
C) diminuiu 10%.
D) aumentou 4%.
E) aumentou 10%.
Questão 10
Se os ângulos internos de um triângulo escaleno são iguais a 6x + 60, 2x + 20 e 4x + 40, podemos afirmar que x é igual a:
A) 4°
B) 5°
C) 6°
D) 8°
E) 10°
Questão 11
Os ângulos internos de um triângulo escaleno são diretamente proporcionais aos números 8, 5 e 2. Podemos afirmar que a medida do menor ângulo é:
A) 20°
B) 24°
C) 36°
D) 42°
E) 60°
Questão 12
Mariana deseja cercar o seu terreno com um muro. Ao realizar um orçamento, ela obteve a informação de que gastaria R$ 180,00 por metro construído. Nessas condições, sabendo que o terreno possui formato de um triângulo escaleno com lados medindo 5 m, 8 m e 12 m, o valor gasto por ela será de:
A) R$ 2800,00
B) R$ 3300,00
C) R$ 3900,00
D) R$ 4500,00
E) R$ 5000,00
Questão 13
Um triângulo escaleno possui ângulos medindo 3x + 49º, x + 11º e x. A medida do maior ângulo é igual a:
A) 109°
B) 86°
C) 75°
D) 64°
E) 20°
Resposta Questão 1
Alternativa B
O perímetro é soma de todos os lados, portanto:
\(x+2+2x\ –5+x –1=36\)
\(4x-4=36\)
\(4x=36+4\ \)
\(4x=40\ \)
\(x=\frac{40}{4}\)
\(x=10\)
O maior lado mede:
2x – 5
\(2\cdot10-5=15\ \) cm
Resposta Questão 2
Alternativa E
O triângulo é considerado um triângulo escaleno se a medida dos seus lados forem todas distintas.
Resposta Questão 3
Alternativa E
Analisando o triângulo, é possível perceber que as medidas dos três lados são distintas, então ele é um triângulo escaleno.
Resposta Questão 4
Alternativa C
Para calcular a área desse triângulo, utilizaremos a fórmula de Heron. Assim, calcularemos o semiperímetro:
\(p=\frac{6+10+8}{2}=\frac{24}{2}=12\)
Calculando a área:
\(A=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
\(A=\sqrt{12\cdot\left(12-6\right)\left(10-6\right)\left(10-8\right)}\)
\(A=\sqrt{12\cdot6\cdot4\cdot2}\)
\(A=\sqrt{6\cdot2\cdot6\cdot4\cdot2}\)
\(A=\sqrt{6^2\cdot2^2\cdot4}\)
\(A=6\cdot2\cdot2=24\ cm^2\)
Resposta Questão 5
Alternativa D
Um triângulo escaleno pode ser triângulo retângulo, acutângulo ou obtusângulo, pois não há restrição nesse sentido, desde que os lados possuam todos medidas distintas.
Resposta Questão 6
Alternativa A
Calculando a área do triângulo:
\(A=\frac{x\cdot\left(x+2\right)}{2}=24\)
\(x^2+2x=24\cdot2\)
\(x^2+2x=48\)
\(x^2+2x-48=0\)
Resolvendo a equação do 2º grau:
\(\Delta=b^2-4ac\)
\(a\ \ =\ 1,\ b=2\ e\ c=-48\)
\(\Delta=2^2-4\cdot1\cdot\left(-48\right)\)
\(\Delta=\ 4\ +192\)
\(\Delta=196\)
\(x=\frac{-b\pm\sqrt\Delta}{2a}\)
\(x=\frac{-2\pm\sqrt{196}}{2\cdot1}\)
\(x=\frac{-2\pm14}{2}\)
\(x_1=\frac{-2+14}{2}=\frac{12}{2}=6\)
\(x_2=\frac{-2-14}{2}=\frac{-16}{2}=-8\)
Como estamos trabalhando com medida de lado, a base mede x=6. Para calcular a altura, temos:
\(h=6+2=8\)
Resposta Questão 7
Alternativa A
Calculando a área, temos:
\(A=\frac{b\cdot h}{2}\)
\(A=\frac{12\cdot5}{2}\)
\(A=\frac{60}{2}\)
\(A=30\ cm^2\)
Resposta Questão 8
Alternativa D
Sendo x a medida do lado desconhecido, temos:
\(x+16+14=43\)
\(x+30=43\)
\(x=43-30\)
\(x=13\)
A medida do lado desconhecido é de 13 cm.
Resposta Questão 9
Alternativa D
Sendo b a base e h a altura, a área é:
\(A=\frac{b\cdot h}{2}\)
Agora, temos:
\(b=1,3b\ \)
\(h=0,8h\ \)
A área nova será:
\(A_N=\frac{1,3b\cdot0,8h}{2}\)
\(A_N=1,04\frac{b\cdot h}{2}\)
Note que:
\(A_N=1,04A\)
Assim, a área nova será 4% maior.
Resposta Questão 10
Alternativa B
Calculando a soma:
\(6x+60+2x+20+4x+40=180°\)
\(12x+120=180°\)
\(12x=180-120\)
\(12x=60\ \)
\(x=\frac{60}{12}\)
\(x=5\ \)
Resposta Questão 11
Alternativa B
Como os ângulos internos são proporcionais aos números 8, 5 e 2, temos:
\(8k+5k+2k=180°\)
\(15k=180°\)
\(k=180°15\)
\(k=12\)
Sabendo que k = 12, o menor ângulo medirá 2k, que é igual a:
\(2\cdot12=24°\)
Resposta Questão 12
Alternativa D
Primeiramente, calcularemos o perímetro:
\(P=5+8+12=25\)
Como cada metro custa 180:
\(180\cdot25=4500,00\)
O valor será de:
R$ 4500,00
Resposta Questão 13
Alternativa A
A soma dos ângulos internos de um triângulo é igual a 180°, portanto:
\(3x+49°+ x+11°+x=180°\)
\(5x+60°=180°\)
\(5x=180°-60°\)
\(5x=120°\)
\(x=120°5\)
\(x=20°\)
O maior ângulo possui:
\(3x+49°\)
\(3\cdot20+49\)
\(60+49=109°\)



