Questão 1
Um triângulo equilátero possui lado medindo 10 metros. Utilizando 1,7 como aproximação para \(\sqrt3\), então a altura desse triângulo é de:
A) 9,5 metros
B) 9,0 metros
C) 8,5 metros
D) 8,0 metros
E) 7,5 metros
Questão 2
Um triângulo equilátero possui perímetro igual a 7,5 metros. Então podemos afirmar que a medida do lado desse triângulo é igual a:
A) 3,0 metros
B) 2,5 metros
C) 2,0 metros
D) 1,5 metro
E) 1,0 metro
Questão 3
Um triângulo é classificado como equilátero quando:
A) possui um ângulo interno medindo 90º.
B) possui a medida de dois lados congruentes entre si e outro lado não congruente.
C) possui os três lados congruentes entre si.
D) possui todos os lados com medidas distintas.
Questão 4
Um terreno possui formato de um triângulo equilátero com altura medindo \(4\sqrt3\) metros. Nessas condições, podemos afirmar que a medida do lado desse terreno, em metros, é igual a:
A) 4
B) 8
C) 12
D) 16
Questão 5
A área de um triângulo equilátero que possui lado medindo 12 cm, em cm², é:
A) \(4\sqrt3\)
B) \(9\sqrt3\)
C) \(12\sqrt3\)
D) \(24\sqrt3\)
E) \(36\sqrt3\)
Questão 6
Um triângulo equilátero possui ângulos internos medindo 2x – 40, 3y + 15 e 6z. Então o valor da expressão x – y – z é:
A) 30
B) 25
C) 15
D) 10
E) 0
Questão 7
Ao analisar os satélites, o Instituto de Nacional de Pesquisas Espaciais (Inpe) notou que a área desmatada se aproximava de um triângulo equilátero. Utilizando 1,73 como aproximação para \(\sqrt3 \), percebeu também que a área desmatada tem área de 692 km². O lado de um triângulo equilátero que possui a área igual à área desmatada deve medir então:
A) 18 quilômetros
B) 20 quilômetros
C) 35 quilômetros
D) 40 quilômetros
E) 55 quilômetros
Questão 8
Dado um triângulo equilátero que possui perímetro igual a \(12\sqrt3\) cm, então a medida da área desse triângulo, em cm², é:
A) \(12\sqrt3\ cm^2\)
B) \(12\ cm^2\)
C) \(16\sqrt3\ cm^2\)
D) \(16\ cm^2\)
E) \(18\ cm^2\)
Questão 9
A medida da altura de um triângulo equilátero que possui área igual a 24 cm² é:
A) 24 cm
B) 32 cm
C) 48 cm
D) 54 cm
E) 64 cm
Questão 10
Sobre o triângulo equilátero, julgue as afirmativas a seguir:
I. Os lados do triângulo equilátero são congruentes.
II. Cada ângulo interno de um triângulo equilátero mede 80º.
III. O triângulo equilátero é um polígono regular.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Questão 11
(Enem 2017) A manchete demonstra que o transporte de grandes cargas representa cada vez mais preocupação quando feito em vias urbanas.
Caminhão entala em viaduto no Centro
Um caminhão de grande porte entalou embaixo do viaduto no cruzamento das avenidas Borges de Medeiros e Loureiro da Silva no sentido Centro-Bairro, próximo à Ponte de Pedra, na capital. Esse veículo vinha de São Paulo para Porto Alegre e transportava três grandes tubos, conforme ilustrado na foto.

Considere que o raio externo de cada cano da imagem seja 0,60 m e que eles estejam em cima de uma carroceria cuja parte superior está a 1,30 m do solo. O desenho representa a vista traseira do empilhamento dos canos.
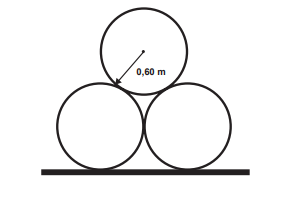
A margem de segurança recomendada para que um veículo passe sob um viaduto é que a altura total do veículo com a carga seja, no mínimo, 0,50 m menor do que a altura do vão do viaduto. Considere 1,7 como aproximação para \(\sqrt3\). Qual deveria ser a altura mínima do viaduto, em metros, para que esse caminhão pudesse passar com segurança sob seu vão?
A) 2,82
B) 3,52
C) 3,70
D) 4,02
E) 4,20
Questão 12
(Enem 2021 PPL) Os alunos do curso de matemática de uma universidade desejam fazer uma placa de formatura, no formato de um triângulo equilátero, em que os seus nomes aparecerão dentro de uma região quadrada, inscrita na placa, conforme a figura.
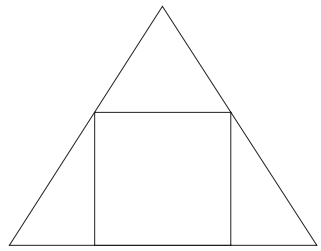
Considerando que a área do quadrado, em que aparecerão os nomes dos formandos, mede 1 m², qual é aproximadamente a medida, em metro, de cada lado do triângulo que representa a placa? (Utilize 1,7 como valor aproximado para \(\sqrt3\).)
A) 1,6
B) 2,1
C) 2,4
D) 3,7
E) 6,4
Resposta Questão 1
Alternativa C
Calculando a altura, sabemos que:
\(h=\frac{l\sqrt3}2\)
\(h=\frac{10⋅1,7}2\)
\(h=\frac{17}2\)
\(h=8,5\)
Então a altura é de 8,5 metros.
Resposta Questão 2
Alternativa B
Sabemos que o perímetro de um triângulo equilátero é a soma dos três lados do triângulo, como esses lados são congruentes, então, ao dividir 7,5 por 3, encontramos a medida do lado do triângulo.
\(7,5∶3=2,5\ m\)
Resposta Questão 3
Alternativa C
O triângulo é equilátero quando possui todos os lados com as mesmas medidas, ou seja, congruentes entre si.
Resposta Questão 4
Alternativa B
Sabemos que:
\(h=\frac{l\sqrt3}2\)
\(4\sqrt3=\frac{l\sqrt3}2\)
\(2⋅4\sqrt3=l\sqrt3\)
\(8\sqrt3=l\sqrt3\)
\(8=l\)
\(l=8\)
Resposta Questão 5
Alternativa E
Calculando a área do triângulo equilátero, temos que:
\(A=\frac{l^2 \sqrt3}4\)
\(A=\frac{12^2 \sqrt3}4\)
\(A=\frac{144 \sqrt3}4\)
\(A=36\sqrt3 \ cm^2\)
Resposta Questão 6
Alternativa B
O triângulo equilátero possui todos os ângulos internos iguais a 60º.
Calculando x:
\(2x-40=60\)
\(2x=60+40\)
\(2x=100\)
\(x=\frac{100}2\)
\(x=50\)
Calculando y:
\(3y+15=60\)
\(3y=60-15\)
\(3y=45\)
\(y=\frac{45}3\)
\(y=15\)
Calculando z:
\(6z=60\)
\(z=\frac{60}6\)
\(z=10\)
Então temos que:
\(x - y - z = 50 - 15 - 10 = 25\)
Resposta Questão 7
Alternativa D
Calculando a área, temos que:
\(A=\frac{l^2 \sqrt3}4\)
\(692=\frac{l^2\cdot1,73}4\)
\(692⋅4=l^2⋅1,73\)
\(2768=l^2⋅1,73\)
\(\frac{2768}{1,73}=l^2\)
\(1600=l^2\)
\(l=\sqrt{1600}\)
\(l=40\ km\)
Resposta Questão 8
Alternativa A
Sabemos que o perímetro é 3 vezes o comprimento do lado do triângulo, sendo assim, temos que:
\(l=12\sqrt3:3=4\sqrt3\)
Se o lado mede \(4\sqrt3\), temos que:
\(A=\frac{l^2 \sqrt3}4\)
\(A=\frac{(4\sqrt3)^2⋅\sqrt3}4\)
\(A=\frac{16⋅3⋅\sqrt3}4\)
\(A=4⋅3\sqrt3\)
\(A=12\sqrt3\)
Resposta Questão 9
Alternativa C
Sabemos que:
\(A=\frac{l^2⋅\sqrt3}4\)
Então temos que:
\(24=\frac{l^2⋅\sqrt3}4\)
\(24⋅4=l^2 \sqrt3\)
\(96=l^2 \sqrt3\)
\(\frac{96}{\sqrt3}=l\)
\(\frac{96\sqrt3}{3}=l\)
\(32\sqrt3=l\)
Calculando a altura:
\(h=\frac{l\sqrt3}2\)
\(h=\frac{32\sqrt3⋅\sqrt3}2\)
\(h=\frac{32⋅3}2\)
\(h=16⋅3\)
\(h=48\ cm\)
Resposta Questão 10
Alternativa B
I. Os lados do triângulo equilátero são congruentes. (Verdadeira)
Por definição, o triângulo equilátero é o triângulo que possui lados congruentes.
II. Cada ângulo interno de um triângulo equilátero mede 80º. (Falsa)
Cada ângulo interno do triângulo equilátero mede 60º.
III. O triângulo equilátero é um polígono regular. (Verdadeira)
Polígono regular é o polígono que possui lados e ângulos congruentes, logo, o triângulo equilátero é, de fato, um polígono regular.
Resposta Questão 11
Alternativa D
Primeiro traçaremos os raios ligando o cento das circunferências, formando um triângulo equilátero de lado igual 1,2 metro:
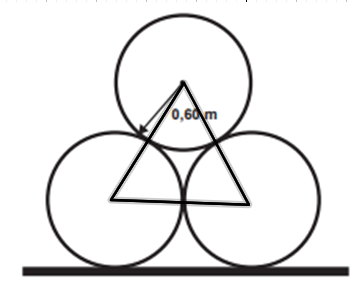
A altura é calculada pela soma da altura do triângulo equilátero, mais dois raios da circunferência, mais 1,3 metro, que é a altura do caminhão. Nesse valor, é necessário somar 0,5 metro, já que a altura da carga deve ser 0,5 metro menor que a altura do viaduto.
Calculando a altura do triângulo equilátero:
\(h=\frac{l\sqrt3}2\)
\(h=\frac{1,2⋅1,7}2\)
\(h=0,6⋅1,7\)
\(h=1,02 \)
Então a altura h será de:
\(1,02 + 0,6 + 0,6 + 1,3 + 0,5 = 4,02\)
Resposta Questão 12
Alternativa B
Analisando a imagem, sabemos que, dentro do triângulo equilátero, há um quadrado e três triângulos.
Podemos observar que, na parte superior, é formado um triângulo equilátero de lados medindo 1 m²:
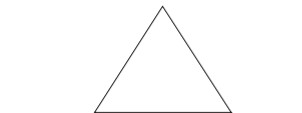
Para calcular a altura h’ desse triângulo, temos que:
\(h'=\frac{l'\sqrt3}{2}\)
\(h'=\frac{1'\sqrt3}{2}\)
\(h'=\frac{\sqrt3}2\)
Sabemos que o triângulo equilátero maior tem altura igual a 1 + h’, logo, temos que:
\(h=1+h'\)
\(h=1+\frac{\sqrt3}2\)
\(h=1+\frac{\sqrt3}2\)
\(h=\frac{2}2+\frac{\sqrt3}2\)
\(h=\frac{2+\sqrt3}2\)
Por outro lado, sabemos que:
\(\frac{l\sqrt3}2=\frac{2+\sqrt3}2\)
\(l\sqrt3=2+\sqrt3\)
Mas sabemos que \(\sqrt3=1,7\):
\(l⋅1,7=2+1,7\)
\(l=\frac{3,7}{1,7}=2,17\)



