Questão 1
Um triângulo retângulo possui os lados perpendiculares medindo 7 cm e 24 cm, então a sua hipotenusa mede:
A) 20 cm
B) 25 cm
C) 32 cm
D) 34 cm
E) 35 cm
Questão 2
A área de serviço de um clube possui formato de retângulo. Nessa área, será colocado um cano para a passagem de esgoto, passando pela diagonal do terreno.
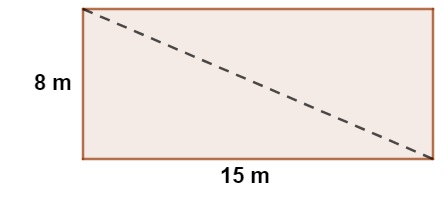
O cano passará pela região que está pontilhada, portanto o comprimento mínimo desse cano, em metros, deve ser de:
A) 16
B) 17
C) 18
D) 19
E) 20
Questão 3
Para realizar a construção de uma praça, a prefeitura traçou as medidas de dois lados da região, que possui formato de triângulo retângulo:
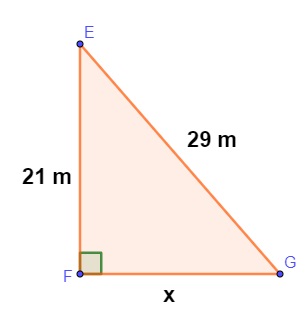
A medida do lado FG, indicada por x, é igual a:
A) 15 m
B) 18 m
C) 20 m
D) 24 m
E) 25 m
Questão 4
Um triângulo retângulo possui hipotenusa medindo 13 m e base medindo 5 m, então a área desse triângulo é igual a:
A) 15 m²
B) 20 m²
C) 25 m²
D) 30 m²
E) 35 m²
Questão 5
O perímetro do triângulo retângulo a seguir, com a medida dos seus lados dada em centímetros, é de:
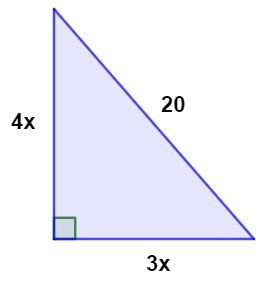
A) 24 cm
B) 48 cm
C) 52 cm
D) 64 cm
E) 96 cm
Questão 6
Um triângulo possui lados medindo 5 cm, 12 cm e 13 cm. Analisando a medida desses lados, podemos afirmar que:
A) esse triângulo é acutângulo.
B) esse triângulo é obtusângulo.
C) esse triângulo é retângulo.
D) esse triângulo é isósceles.
Questão 7
Um triângulo retângulo possui área igual a 24 cm². Sabendo que a sua base mede 6 cm, a medida da hipotenusa é:
A) 4 cm
B) 6 cm
C) 8 cm
D) 10 cm
E) 12 cm
Questão 8
Um terreno possui formato de triângulo retângulo com lados perpendiculares medindo 8 e 15 metros. Deseja-se cercar esse terreno com arame. Para cada metro de cerca serão gastos R$ 12,00. Assim, o valor gasto para cercar o terreno todo será de:
A) R$ 204,00
B) R$ 276,00
C) R$ 400,00
D) R$ 480,00
E) R$ 520,00
Questão 9
(Instituto Avança São Paulo) Em uma jogada ensaiada, o jogador A passa a bola para o jogador B, que passa para o jogador C. Considerando que a trajetória da bola é linear e eles estão parados em seus lugares, qual é o total da distância percorrida pela bola nessa jogada?
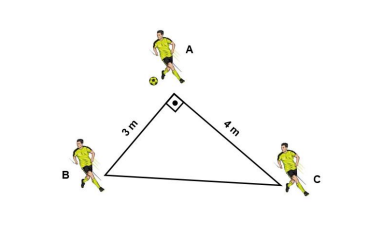
A) 3 m
B) 4 m
C) 5 m
D) 7 m
E) 8 m
Questão 10
(Instituto Avança São Paulo) Deseja-se subir em um muro com 32 metros de altura. Para isso, apoia-se uma escada a 24 metros de distância desse muro, como pode ser observado na figura abaixo.
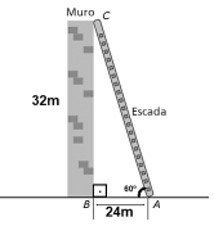
Desse modo, a altura dessa escada, em metros, é de:
A) 28 m.
B) 30 m.
C) 40 m.
D) 45 m.
E) 56 m.
Questão 11
(Enem 2014) Diariamente, uma residência consome 20.160Wh. Essa residência possui 100 células solares retangulares (dispositivos capazes de converter a luz solar em energia elétrica) de dimensões 6 cm x 8 cm. Cada uma das tais células produz, ao longo do dia, 24Wh por centímetro de diagonal. O proprietário dessa residência quer produzir, por dia, exatamente a mesma quantidade de energia que sua casa consome. Qual deve ser a ação desse proprietário para que ele atinja o seu objetivo?
A) Retirar 16 células.
B) Retirar 40 células.
C) Acrescentar 5 células.
D) Acrescentar 20 células.
E) Acrescentar 40 células.
Questão 12
(Instituto Excelência) De acordo com a definição básica do teorema de Pitágoras, assinale a alternativa CORRETA:
A) O teorema de Pitágoras relaciona as medidas dos catetos de um triângulo retângulo à medida de sua hipotenusa. O teorema de Pitágoras diz que “a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”.
B) O teorema de Pitágoras pode ser determinado pela seguinte lei de correspondência: “Feixes de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes.”
C) O teorema de Pitágoras pode ser utilizado para fazer a divisão de polinômios. Para fazer a divisão de um polinômio P(x) por outro polinômio Q(x), é fundamental que o polinômio Q(x) seja da forma x + u ou x – u, isto é, deve ser um binômio de 1º grau.
D) Nenhuma das alternativas.
Resposta Questão 1
Alternativa B
Aplicando o teorema de Pitágoras e utilizando x para representar a medida da hipotenusa:
x² = 7² + 24²
x² = 49 + 576
x² = 625
\(x=\sqrt{625}\)
x = 25
Resposta Questão 2
Alternativa B
Sabendo que ao traçar a diagonal de um retângulo o dividimos em dois triângulos retângulos, podemos encontrar o comprimento mínimo do cano x aplicando o teorema de Pitágoras:
\(x^2=8^2+{15}^2\)
\(x^2=64+225\)
\(x^2=289\)
\(x=\sqrt{289}\)
\(x\ =\ 17\ m\ \)
Resposta Questão 3
Alternativa C
Sabemos que a hipotenusa é igual a 29 metros e que um dos catetos mede 21 metros, então a medida de x é:
\({29}^2={21}^2+x^2\)
\(841=441+x^2\)
\(841-441=x^2\)
\(x^2=400\)
\(x=\sqrt{400}\)
\(x=20\)
Resposta Questão 4
Alternativa D
Seja h a altura do triângulo, sabendo que ela é um dos catetos, temos que:
\(5^2+h^2={13}^2\)
\(25+h^2=169\)
\(h^2=169-25\)
\(h^2=144\)
\(h=\sqrt{144}\)
\(h=12\)
Considerando a altura de 12 metros, calcularemos a área desse triângulo:
\(A=\frac{b\cdot h}{2}\)
\(A=\frac{5\cdot12}{2}\)
\(A=\frac{60}{2}\)
\(A=30{\ m}^2\)
Resposta Questão 5
Alternativa B
Primeiramente, calcularemos o valor de x, aplicando o teorema de Pitágoras:
(3x)² + (4x)² = 20²
9x² + 16x² = 400
25x² = 400
x² = 400 : 25
x² = 16
x = \(\sqrt{16}\)
x = 4
Sabendo o valor de x, para calcular o perímetro temos que:
\(P=3x+4x+20\ \)
\(P=3\cdot4+4\cdot4\ +20\ \)
\(P=12+16+20\)
\(P=48\ cm\)
Resposta Questão 6
Alternativa C
Para verificar se um triângulo é retângulo, é necessário averiguar a aplicação de teorema de Pitágoras. Supondo que esse triângulo seja retângulo, temos que 13 é a hipotenusa e que 5 e 12 são os catetos:
13² = 12² + 5²
169 = 144 + 25
169 = 169
Como é possível verificar que o teorema de Pitágoras é válido para esse triângulo, podemos afirmar que ele é um triângulo retângulo.
Resposta Questão 7
Alternativa D
Sabemos que a fórmula da área de um triângulo é:
\(A=\frac{b\cdot h}{2}\)
Como a base mede 6 cm, encontraremos a altura desse triângulo:
\(24=\frac{6\cdot h}{2}\)
\(24\cdot2=6\cdot h\)
\(48=6\cdot h\)
\(h=\frac{48}{6}\)
\(h\ =\ 8\ \)
Se a altura mede 8 cm, os catetos medem 6 cm e 8 cm. Logo, pelo teorema de Pitágoras, utilizando x para a hipotenusa temos que:
x ² = 6² + 8²
x² = 36 + 64
x² = 100
\(x=\sqrt{100}\)
x = 10 cm
Resposta Questão 8
Alternativa D
De início, calcularemos a medida da hipotenusa x desse triângulo:
x² = 8² + 15²
x² = 64 + 225
x² = 289
x = \(\sqrt{289}\)
x = 17
A soma dos lados desse triângulo é igual a:
P = 17 + 15 + 8 = 40
Como cada metro custa R$ 12,00, temos que:
\(40\ \cdot12\ =\ 480\)
Logo, serão gastos R$ 480,00.
Resposta Questão 9
Alternativa E
Calcularemos a distância entre os jogadores B e C e somaremos com 3, que é a distância entre os jogadores A e B.
Pelo teorema de Pitágoras temos que:
BC² = 3² + 4²
BC² = 9 + 16
BC² = 25
BC = \(\sqrt{25}\)
BC = 5
Portanto:
AB + BC = 3 + 5 = 8 m
Resposta Questão 10
Alternativa C
Seja x a altura da escada, aplicando o teorema de Pitágoras temos que:
x² = 32² + 24²
x² = 1024 + 576
x² = 1600
x = \(\sqrt{1600}\)
x = 40 m
Resposta Questão 11
Alternativa A
Calculando a diagonal, pelo teorema de Pitágoras temos que:
d² = 6² + 8²
d² = 36 + 64
d² = 100
d = √100
d = 10
Logo, cada célula produz:
10 · 24 = 240 Wh
Sabemos que existem 100 células, então será produzido o total de:
100 · 240 = 24000 Wh
O consumo excedente é calculado por:
24000 – 21160 = 3840 Wh
Portanto:
3840 : 240 = 16
Assim, devem ser retiradas 16 células.
Resposta Questão 12
Alternativa A
O teorema de Pitágoras, de fato, relaciona as medidas dos catetos de um triângulo retângulo à medida de sua hipotenusa, pois “a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”.



