.jpg "Exemplo do teorema fundamental da semelhança no triângulo ABC")
Questão 2
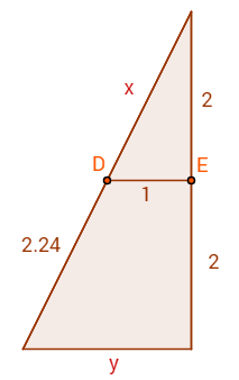
Determine o valor de x e de y na figura abaixo sabendo que o segmento DE é paralelo à base do triângulo.
Questão 3
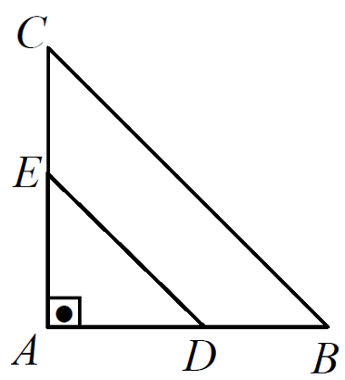
(UNIMONTES MG/2015) Na figura abaixo, AD = 1, AB = a , AE = b e os segmentos DE e BC são paralelos. Com base nessas informações, é CORRETO afirmar que AC vale:
a) a
b
b) b
a
c) a + b
d) ab
Questão 4
(UEA AM/2014) Potencialmente, os portos da região Norte podem ser os canais de escoamento para toda a produção de grãos que ocorre acima do paralelo 16 Sul, onde estão situados gigantes do agronegócio. Investimentos em logística e a construção de novos terminais portuários privados irão aumentar consideravelmente o número de toneladas de grãos embarcados anualmente.
Suponha que dois navios tenham partido ao mesmo tempo de um mesmo porto A, em direções perpendiculares e a velocidades constantes. Sabe-se que a velocidade do navio B é de 18 km/h e que, com 30 minutos de viagem, a distância que o separa do navio C é de 15 km, conforme mostra a figura:
Teorema fundamental da semelhança no movimento perpendicular entre navios
Desse modo, pode-se afirmar que, com uma hora de viagem, a distância, em km, entre os dois navios e a velocidade desenvolvida pelo navio C, em km/h, serão, respectivamente,
a) 30 e 25.
b) 25 e 22.
c) 30 e 24.
d) 25 e 20.
e) 25 e 24.
Resposta Questão 1
Utilizando o teorema fundamental da semelhança, teremos:
2 + 2 = 2 + x
2 2
Realizando a multiplicação cruzada, teremos:
2·4 = 2·(2 + x)
Calculando o lado esquerdo e utilizando a propriedade distributiva da multiplicação (chuveirinho) no lado direito da equação, teremos:
8 = 4 + 2x
Reorganizando os termos dessa equação e multiplicando-a por (-1), obteremos:
2x = 8 – 4
2x = 4
x = 4
2
x = 2
Resposta Questão 2
Utilizando o teorema de Tales, podemos escrever:
2 = x
2 2,24
Realizando a multiplicação cruzada, obteremos:
2,24·2 = 2·x
Pela lei do corte, teremos:
x = 2,24
Utilizando o teorema fundamental da semelhança, teremos:
2 = 1
2 + 2 y
Após a multiplicação cruzada e realização dos cálculos resultantes, obteremos:
2y = 4
y = 4
2
y = 2
Logo, os valores de x e y são 2,24 e 2, respectivamente.
Resposta Questão 3
Utilizando o teorema fundamental da semelhança, teremos:
AD = AE
AB AC
Substituindo os valores dos segmentos, obteremos:
1 = b
a AC
Utilizando multiplicação cruzada, o resultado será:
AC = ab
Letra D.
Resposta Questão 4
A velocidade do navio B é de 18 km/h e, em meia hora, ele se deslocou a metade de 18 km.
Portanto, na primeira meia hora, o navio B estava 9 km distante do porto A. Dessa maneira, y = 9.
Com uma hora de viagem, a distância do navio B até o porto é de 18 km, já que sua velocidade é 18 km/h.
Sejam B' e C' os pontos onde os navios B e C, respectivamente, encontravam-se na primeira meia
hora de viagem. Utilizando o teorema fundamental da semelhança, podemos escrever:
AB' = B'C'
AB BC
Substituindo os valores dos segmentos:
9 = 15
18 BC
A multiplicação cruzada garante o seguinte resultado:
9BC = 18·15
BC = 270
9
BC = 30
BC é a distância entre os navios B e C. Como os navios movem-se em direções perpendiculares, a velocidade do Navio C pode ser calculada pelo teorema de Pitágoras. Note que a velocidade média de um objeto em movimento é dada pela distância percorrida pelo objeto (ou que seria percorrida) em uma hora. Portanto, pelo teorema de Pitágoras:
BC2 = AB2 + AC2
302 = 182 + AC2
900 = 324 + AC2
900 – 324 = AC2
576 = AC2
AC = √576
AC = 24
Portanto, o Navio C moveu-se 24 km em uma hora, logo, sua velocidade média é de 24 km/h.
Letra C.
