Questão 1
Calcule a soma dos ângulos internos de um triângulo qualquer e de um retângulo qualquer.
Questão 3
(UNIFESP - 2003) Pentágonos regulares congruentes podem ser conectados lado a lado, formando uma estrela de cinco pontas, conforme destacado na figura a seguir
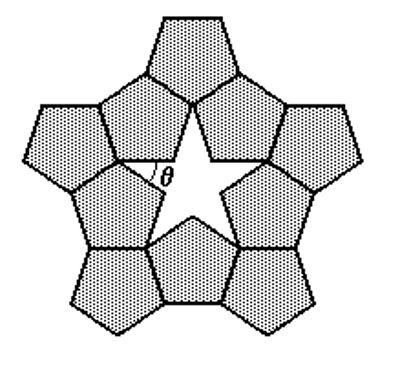
Nessas condições, o ângulo θ mede:
a) 108°.
b) 72°.
c) 54°.
d) 36°.
e) 18°.
Questão 4
(FAAP-97) A medida mais próxima de cada ângulo externo do heptágono regular da moeda de R$ 0,25 é:
.jpg)
a) 60°
b) 45°
c) 36°
d) 83°
e) 51°
Resposta Questão 1
Independentemente do polígono a que o exercício ou situação se refira, a soma dos seus ângulos internos tem valor fixo e é dada pela fórmula S = (n – 2)·180, em que n é o número de lados do polígono. Logo,
Soma dos ângulos internos do triângulo:
S = (3 – 2)·180
S = 1·180
S = 180°
Qualquer que seja o triângulo, a soma de seus ângulos internos sempre será igual a 180°. Isso pode ser usado quando conhecemos as medidas de dois dos ângulos internos de um triângulo e é necessário calcular o valor da última.
Soma dos ângulos internos de um retângulo:
S = (4 – 2)·180
S = 2·180
S = 360°
Não só retângulos, mas qualquer que seja o quadrilátero, a soma de seus ângulos internos será 360°.
Resposta Questão 2
A soma dos ângulos internos de um quadrilátero é dada por:
S = (n – 2)·180
Sabendo que o número de lados da figura é 4, basta substituir n por 4:
S = (4 – 2)·180
S = 2·180
S = 360°
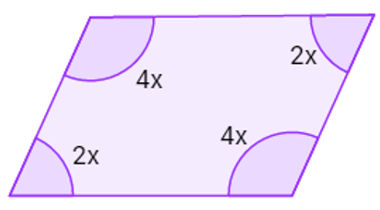
Agora some os ângulos internos dessa figura e iguale o resultado a 360°:
2x + 4x + 2x + 4x = 360
12x = 360
x = 360
12
x = 30
Agora basta substituir x em cada ângulo para descobrir os seus valores.
4x = 4·30 = 120° e
2x = 2·30 = 60°
Os ângulos são 120° e 60°.
Resposta Questão 3
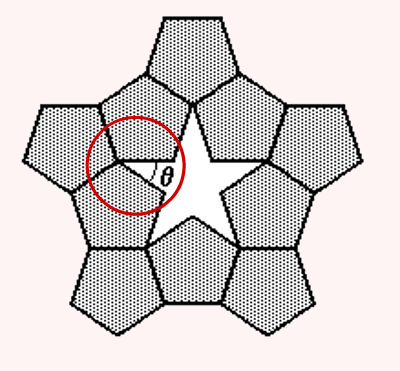
Na ponta da estrela onde está destacado o ângulo θ, temos o encontro de três ângulos internos de pentágonos regulares. Para descobrir a medida de cada um desses ângulos, basta calcular a soma dos ângulos internos do pentágono e dividir por 5.
A fórmula para calcular a soma dos ângulos internos de um polígono é:
S = (n – 2)·180
*n é o número de lados do polígono. No caso desse exercício:
S = (5 – 2)·180
S = 3·180
S = 540
Dividindo a soma dos ângulos internos por 5, pois um pentágono possui cinco ângulos internos, encontraremos 108° como medida de cada ângulo interno.
Observe na imagem anterior que a soma de três ângulos internos do pentágono com o ângulo θ tem como resultado 360°.
108 + 108 + 108 + θ = 360
324 + θ = 360
θ = 360 – 324
θ = 36°
Letra D.
Resposta Questão 4
Heptágonos são figuras geométricas que possuem sete lados, sete vértices e sete ângulos. Como esse heptágono é regular, então todos os seus ângulos e lados possuem a mesma medida.
A soma dos ângulos internos do heptágono é:
S = (n – 2)·180
S = (7 – 2)·180
S = 5·180
S = 900°
Cada ângulo interno do heptágono regular mede a soma dos ângulos internos dividida por 7.
900 = 128,57
7
Agora, resta apenas descobrir o valor de um ângulo externo. Os ângulos externos de um polígono são suplementares aos ângulos internos respectivos. Portanto, a soma entre um ângulo interno e seu ângulo externo tem como resultado 180°. Dessa forma, os ângulos externos da moeda de 25 centavos medem:
128,57 + x = 180
x = 180 – 128,57
x = 51,43°
Letra E.