Exercícios sobre sólidos geométricos

(Enem 2017) Uma rede hoteleira dispõe de cabanas simples na ilha de Gotland, na Suécia, conforme Figura 1. A estrutura de sustentação de cada uma dessas cabanas está representada na Figura 2. A ideia é permitir ao hóspede uma estada livre de tecnologia, mas conectada com a natureza.

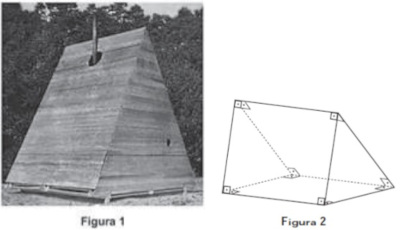
A forma geométrica da superfície cujas arestas estão representadas na Figura 2 é:

A) tetraedro

B) pirâmide retangular

C) tronco de pirâmide retangular

D) prisma quadrangular reto

E) prisma triangular reto

(Vunesp 2019) Analise o sólido geométrico da figura:

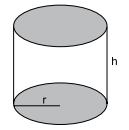
Se h = 48 cm e r = 17 cm, esse sólido tem volume igual a: (use π = 3,14)

A) 0,082 m³

B) 0,068 m³

C) 0,123 m³

D) 0,044 m³

E) 0,246 m³

(Objetiva 2019) Certo paralelepípedo possui as seguintes dimensões: 10 cm de comprimento, 5 cm de largura e 5 cm de altura. Qual o volume total desse paralelepípedo:

A) 50 cm³

B) 150 cm³

C) 250 cm³

D) 350 cm³

(Enem 2020) Uma das Sete Maravilhas do Mundo Moderno é o Templo de Kukulkán, localizado na cidade de Chichén Itzá, no México. Geometricamente, esse templo pode ser representado por um tronco reto de pirâmide de base quadrada. As quantidades de cada tipo de figura plana que formam esse tronco de pirâmide são:

A) 2 quadrados e 4 retângulos.

B) 1 retângulo e 4 triângulos isósceles.

C) 2 quadrados e 4 trapézios isósceles.

D) 1 quadrado, 3 retângulos e 2 trapézios retângulos.

E) 2 retângulos, 2 quadrados e 2 trapézios retângulos.

Constantemente nos deparamos com sólidos geométricos no dia a dia. Entre os sólidos geométricos, estão aqueles conhecidos como poliedros, que possuem faces formadas por polígonos. Dos sólidos geométricos seguintes, todos eles são poliedros, exceto:

A) Tronco da pirâmide

B) Cubo

C) Pirâmide

D) Cone

E) Prisma de base pentagonal

Um contêiner comum, ou seja, em formato de paralelepípedo retângulo, é um equipamento bastante utilizado para o transporte de cargas. Devido a sua grande exposição às mudanças climáticas, frequentemente ele passa por manutenções. Em uma empresa de transporte, um contêiner possui altura de 2,5 metros, comprimento de 6 metros e largura de 2,4 metros. Devido ao longo tempo de uso desse equipamento, ele precisará passar por uma manutenção em que toda a sua área externa será lixada e pintada novamente. Para fazer o orçamento desse serviço, é necessário calcular a área total do contêiner, que é de:

A) 65,6 m³

B) 70,8 m³

C) 71,2 m³

D) 75,4 m³

E) 78,0 m³

As planificações de três sólidos estão representadas a seguir:

Analisando as imagens, os sólidos geométricos formados são, respectivamente:

A) prisma de base pentagonal, cilindro e cubo.

B) prisma de base retangular, cone e pirâmide de base quadrada.

C) cubo, esfera e prisma de base triangular.

D) prisma de base hexagonal, cone e pirâmide de base quadrada.

E) paralelepípedo, cone e tetraedro.

Uma fábrica de cosméticos produz frascos de perfumes semanalmente para atender as demandas da região. Na busca por inovação e economia, a fábrica decidiu implantar novos frascos para os perfumes produzidos por ela. Para isso, ela decidiu investir em frascos que possuem o formato cilíndrico, com raio igual a 4 cm e altura igual a 7 cm, sabendo que cada centímetro quadrado de embalagem custa R$ 0,25. Além disso, a fábrica gasta R$ 2 para cada 6 mL de perfume no frasco. Supondo que o frasco tenha todo o seu volume ocupado e sabendo que esse perfume é vendido diretamente pela fábrica pelo valor de R$ 299,90, o lucro obtido em cada frasco de perfume será de: (use π = 3)

A) R$ 112,00

B) R$ 178,25

C) R$ 121,65

D) R$ 187,90

E) R$ 239,45

Na decoração de uma casa, foi colocado um pequeno aquário que possui formato de um cubo, cuja soma das arestas é igual a 180 cm. Sabendo que esse ambiente será planejado de tal forma que exista um espaço no armário correspondente à capacidade do aquário, e supondo que a espessura do vidro seja desprezível, o volume do aquário em litros será igual a:

A) 3,2 L

B) 3,4 L

C) 3,5 L

D) 4,3 L

E) 4,5 L

Das alternativas seguintes, escolha aquela que não representa um corpo redondo.

A) esfera

B) cone

C) cilindro

D) circulo

E) tronco de cone

Com a pandemia de covid-19, muitas pessoas ficaram impossibilitadas de trabalhar fora de casa para conter a disseminação do vírus. Na busca da complementação da renda familiar, muitas delas começaram a trabalhar com a venda de alimentos produzidos dentro de suas casas. Um caso desses é o da Mariana, que resolveu trabalhar com a venda de salada de frutas dentro de seu condomínio. Para realizar suas vendas, ela tinha duas opções de recipientes de plástico, representados a seguir:

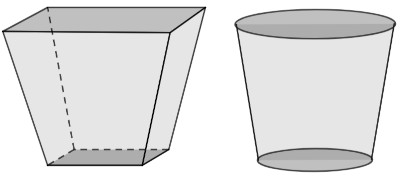
Os recipientes possuem, respectivamente, formato de:

A) prisma de base retangular e cilindro

B) pirâmide e cone

C) tronco de pirâmide e tronco de cone

D) paralelepípedo e cilindro

E) cubo e cilindro

Sobre os sólidos geométricos, julgue as afirmativas a seguir como verdadeiras ou falsas:

I – Os sólidos geométricos são divididos em poliedros e corpos redondos.

II – Pirâmides e trapézios são exemplos de poliedros.

III – Esfera e cone são exemplos de corpos redondos.

Podemos afirmar que:

A) Somente I e II estão corretas.

B) Somente II e III estão corretas.

C) Somente I e III estão corretas.

D) Todas estão corretas.

E) Todas estão incorretas