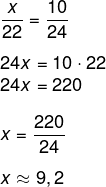Questão 1
Sobre os triângulos semelhantes, julgue as afirmativas a seguir.
I → Ao comparar os triângulos ABC e DEF, eles serão semelhantes se os seus lados forem proporcionais.
II → Os lados de dois triângulos semelhantes são necessariamente congruentes.
III → Se existem dois triângulos congruentes, então eles são semelhantes.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas I e III são verdadeiras.
E) Somente as afirmativas II e III são verdadeiras.
Questão 2
Renata quer calcular a altura da sua caixa d’água. Para isso, durante o dia, ela observou a sombra de um pedaço de madeira reto ao lado da caixa d’água e mediu o comprimento da sombra, que era de 0,6 metro. Já a sombra da caixa d’água era de 3,40 metros, conforme a imagem a seguir:
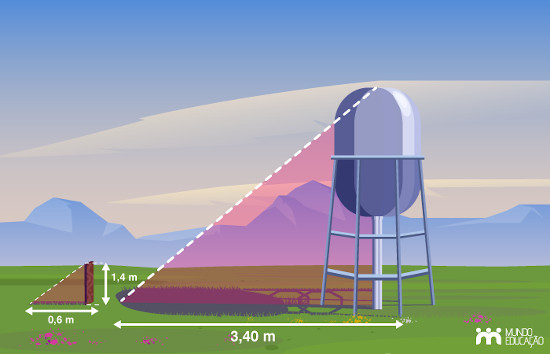
Sabendo que a altura do pedaço de madeira era de 1,4 metro, então a altura da caixa d’água é de:
A) 9,1 metros.
B) 8,5 metros.
C) 8,2 metros.
D) 8,0 metros.
E) 7,9 metros.
Questão 3
Dado o triângulo a seguir e sabendo que o segmento DE é paralelo à base CB e que AC mede 10 cm, AD mede 4 cm e AE é igual a 5 cm, então podemos afirmar que o segmento BE mede:
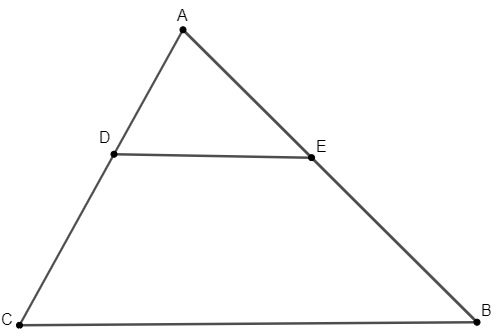
A) 11 cm.
B) 10,5 cm.
C) 9,5 cm.
D) 8,0 cm.
E) 7,5 cm.
Questão 4
(Enem 2013) O dono de um sítio pretende colocar uma haste de sustentação para melhor firmar dois postes de comprimentos iguais a 6 m e 4 m. A figura representa a situação real na qual os postes são descritos pelos segmentos AC e BD e a haste é representada pelo segmento EF, todos perpendiculares ao solo, que é indicado pelo segmento de reta AB. Os segmentos AD e BC representam cabos de aço que serão instalados.
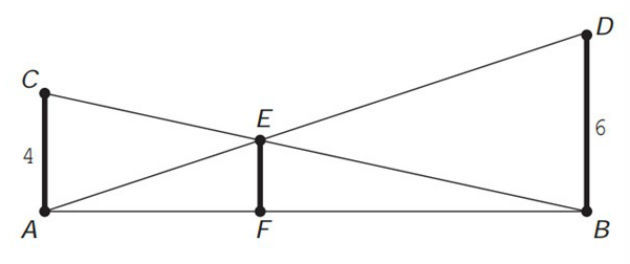
Qual deve ser o valor do comprimento da haste EF?
A) 1 m
B) 2 m
C) 2,4 m
D) 3 m
E) 2√6 m
Questão 5
Os triângulos ABC e DFE são triângulos semelhantes. Sabendo que a razão de semelhança entre os triângulos ABC e DFE é 2, então a soma do perímetro desses triângulos é igual a:
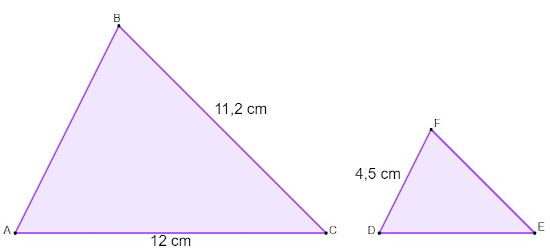
A) 16, 1 cm
B) 32, 2 cm
C) 36,4 cm
D) 48,3 cm
E) 52,9 cm
Questão 6
(PUC-Campinas) Os triângulos MIL e MKJ, representados na figura a seguir, são semelhantes, sendo os ângulos L e J congruentes.
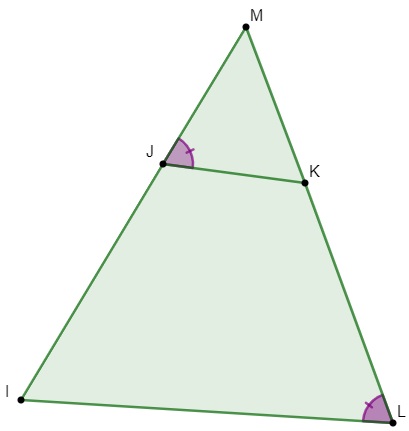
Se IL = 16 cm, ML = 20 cm, MJ = 10 cm e MK = 10,4 cm, o perímetro do quadrilátero ILKJ, em centímetros, é:
A) 32,6.
B) 36,4.
C) 40,8.
D) 42,6.
E) 44,4.
Questão 7
Analisando os triângulos, podemos afirmar que:
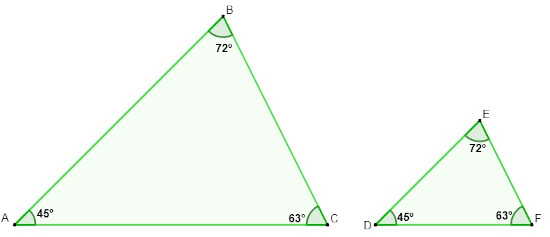
A) Eles são semelhantes por terem lados congruentes e ângulos congruentes.
B) Eles são semelhantes por terem ângulos congruentes e lados congruentes.
C) Eles são congruentes pelo caso lado, lado e lado.
D) Eles são congruentes pelo caso ângulo, lado e ângulo.
E) Eles não são congruentes pelo caso ângulo, ângulo e ângulo.
Questão 8
(Unesp) A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:
A) 25
B) 29
C) 30
D) 45
E) 75
Questão 9
Analisando os triângulos BCD e EFD a seguir e sabendo que a medida dos seus lados foi dada em centímetros, então a medida do segmento FC é igual a:
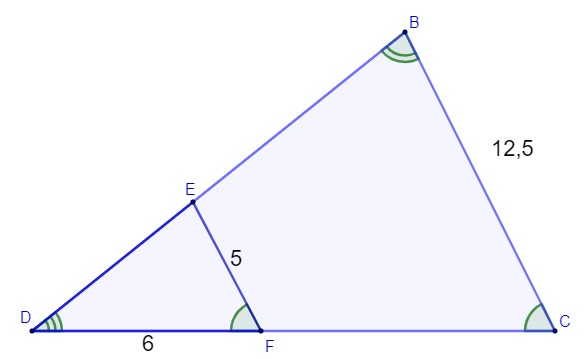
A) 6 cm.
B) 8 cm.
C) 9 cm.
D) 10 cm.
E) 15 cm.
Questão 10
(Cefet 2015) A ilustração a seguir representa uma mesa de sinuca retangular, de largura e comprimento iguais a 1,5 e 2,0 m, respectivamente. Um jogador deve lançar a bola branca do ponto B e acertar a preta no ponto P, sem acertar em nenhuma outra, antes. Como a amarela está no ponto A, esse jogador lançará a bola branca até o ponto L, de modo que a mesma possa rebater e colidir com a preta.
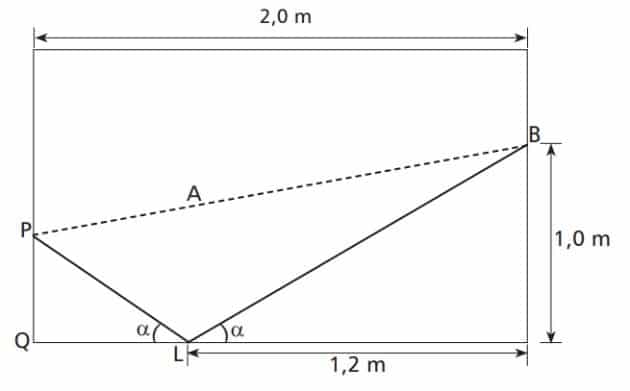
Se o ângulo da trajetória de incidência da bola na lateral da mesa e o ângulo de rebatimento são iguais, como mostra a figura, então a distância de P a Q, em cm, é aproximadamente:
A) 67
B) 70
C) 74
D) 81
Questão 11
Analisando os triângulos a seguir, sabendo que AB é paralelo a DC, então podemos afirmar que x é igual a:
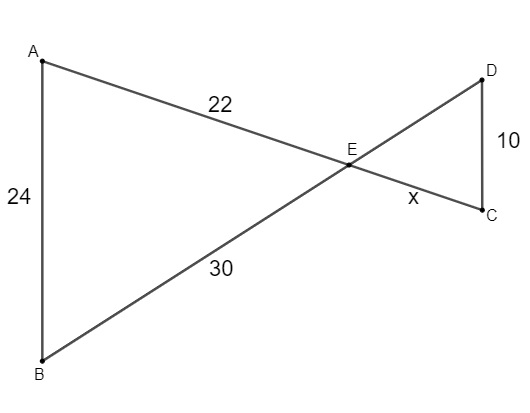
A) 9,2
B) 9,6
C) 10, 5
D) 10,8
E) 11,0
Questão 12
Sobre a semelhança de triângulos, julgue as afirmativas a seguir:
I → Dois triângulos retângulos sempre serão semelhantes.
II → Os triângulos são semelhantes quando um deles é ampliação ou redução do outro, sem nenhuma distorção nos seus lados e ângulos.
III → É possível que dois triângulos não sejam semelhantes mesmo tendo dois ângulos congruentes.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente a afirmativa I é falsa.
E) Somente a afirmativa II é falsa.
Resposta Questão 1
Alternativa D.
I → Verdadeira. Para que os triângulos sejam semelhantes, os lados devem ser proporcionais.
II → Falsa. Para que os triângulos sejam semelhantes, os lados podem não ser congruentes.
III → Verdadeira, pois dois triângulos congruentes também são semelhantes.
Resposta Questão 2
Alternativa E.
Os triângulos são semelhantes, pois os ângulos internos são congruentes. Então, seja x a altura da caixa d’água, por semelhança de triângulos, temos que:
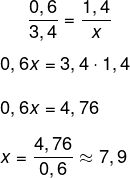
Resposta Questão 3
Alternativa E.
Como as bases são paralelas, o triângulo ADE é semelhante ao triângulo ACB.
Por semelhança, primeiro encontraremos o valor de AB, logo:
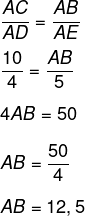
Sabemos que AB = AE + BE, logo:
12,5 = 5 + BE
12,5 – 5 = BE
7,5 = BE
BE = 7,5
Resposta Questão 4
Alternativa C.
Os triângulos FEB e ACB são semelhantes, pois os seus ângulos são congruentes, então:
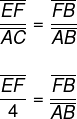
Por outro lado, os triângulos FEA e BDA também são semelhantes, pois os ângulos são congruentes, logo podemos escrever a seguinte razão:
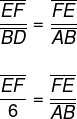
Somando a primeira com a segunda razão, temos que:
![]()
Mas FE + FB = AB:
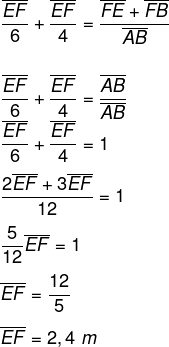
Resposta Questão 5
Alternativa D.
Como a razão de proporção é igual a 2, os lados do triângulo maior são o dobro dos lados do triângulo menor.
Então, vamos encontrar o lado AB do triângulo maior:
AB = 2FD
AB = 2 · 4,5
AB = 9
O perímetro do triângulo maior (PM) é:
PM = 12 + 11,2 + 9 = 32,2
Como os lados do triângulo menor são metade dos lados do triângulo maior, consequentemente o perímetro do triângulo menor (Pm) será metade do perímetro do triângulo maior, ou seja:
32,2 : 2 = 16,1 cm
Então, a soma dos perímetros é:
32,2 + 16,1 = 48,3 cm
Resposta Questão 6
Alternativa E.
O perímetro é a soma de todos os lados:
P = IL + LK + KJ + IJ
Conhecemos o valor de IL = 16:
P = 16 + LK + KJ + IJ
Sabemos também que:
LK = ML – MK
LK = 20 – 10,4
LK = 9,6
Para encontrar KJ, temos que:
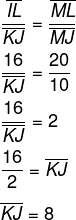
Para encontrar o valor de IJ, temos que:
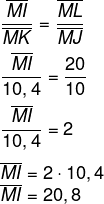
Pelo valor de MI, podemos encontrar IJ, pois
MI = IJ + MJ
20,8 = IJ + 10
20,8 – 10 = IJ
IJ = 10,8.
Logo, o perímetro P é:
P = 16 + 9,6 + 8 + 10,8 = 44,4 cm
Resposta Questão 7
Alternativa B.
Podemos perceber que eles possuem três ângulos iguais, porém a medida dos lados não é a mesma, pois o triângulo ABC possui lados maiores que o triângulo DEF, então eles são semelhantes pelo fato de possuírem ângulos congruentes. Podemos concluir então que eles são semelhantes por terem ângulos congruentes e lados não congruentes.
Resposta Questão 8
Alternativa A.
Podemos representar a situação por meio de um desenho:

Seja x a altura do prédio, por semelhança de triângulos, temos que:
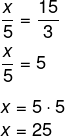
Resposta Questão 9
Alternativa C.
Os triângulos possuem ângulos congruentes, logo eles são semelhantes.
Primeiro encontraremos o comprimento do lado CD:
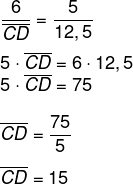
Sabemos que CD = DF + FC:
15 = 6 + FC
15 – 6 = FC
9 = FC
FC = 9
Resposta Questão 10
Alternativa A.
Sabemos que a base do retângulo mede 2 metros, então:
QL = 2 – 1,2 = 0,8
Conhecendo o valor de QL, por semelhança de triângulos, temos que:
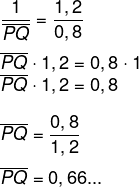
Como a medida está em metros, vamos multiplicar por 100 para transformá-la em centímetros:
PQ = 0,66… · 100
PQ = 66,66…
Arredondando, temos que:
PQ = 67
Resposta Questão 12
Alternativa B.
I → Falsa.
Dois triângulos retângulos podem ou não ser semelhantes, dependendo da medida dos seus demais ângulos e lados.
II → Verdadeira.
Se ampliarmos ou reduzirmos o triângulo de forma proporcional, ele será semelhante ao triângulo anterior.
III → Falsa.
Se dois ângulos são congruentes, então os triângulos são semelhantes.