Exercícios sobre retas paralelas

Sobre as posições relativas entre retas, uma das classificações é a de retas paralelas. Duas retas pertencentes a um mesmo plano são classificadas como paralelas quando

A) têm um único ponto em comum.

B) têm somente dois pontos em comum.

C) têm infinitos pontos em comum.

D) não têm ponto em comum.

Quando há duas retas pertencentes ao mesmo plano, elas podem ter três posições possíveis. A seguir, faça a correspondência correta entre os tipos de reta e suas respectivas características.

I. Concorrentes

II. Coincidentes

III. Paralelas

(     ) têm infinitos pontos em comum.

(     ) têm um único ponto em comum.

(     ) não têm nenhum ponto em comum.

Agora marque a alternativa que represente a correspondência correta.

A) I, II e III

B) II, III e I

C) II, I e III

D) III, II e I

E) III, I e II

Duas retas, pertencentes a um mesmo plano, que não possuem pontos em comum são conhecidas como:

A) transversais

B) concorrentes

C) coincidentes

D) paralelas

E) incidentes

(Vunesp) Em um livro didático, consta a seguinte figura:

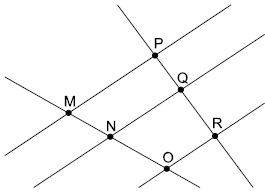
Sobre essa figura, há informações, no livro, de que as retas que contêm os pontos M e P, N e Q, e O e R são paralelas, e que as medidas dos segmentos de extremidades MN, PQ e PR, em certa unidade de medida u, são iguais a 5 u, 4 u e 9 u respectivamente.
Como exercício, é solicitado que o aluno determine a medida do segmento NO, na unidade de medida u, cuja resposta correta é:

A) 5,25

B) 5,50

C) 5,75

D) 6,00

E) 6,25

Foram traçadas três retas paralelas e duas retas transversais, conforme a imagem a seguir:

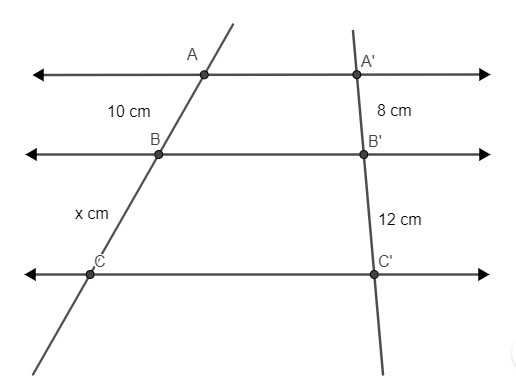
Utilizando o teorema de Tales, podemos afirmar que o segmento BC mede:

A) 10 cm

B) 12 cm

C) 15 cm

D) 16 cm

E) 18 cm

Analise a imagem a seguir:

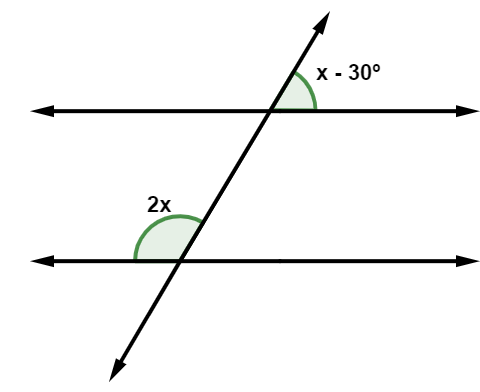
Podemos afirmar que o valor do ângulo agudo é:

A) 70º

B) 60º

C) 50º

D) 40º

E) 30º

(Marinha) Duas retas paralelas r e s são cortadas por uma reta transversal, formando, no mesmo plano, dois ângulos obtusos alternos internos que medem (\(\frac{x}{2} + 30°\)) e (\(\frac{3x}{5} + 15°\)). Então o suplemento de um desses ângulos mede:

A) 75º

B) 80º

C) 82º

D) 85º

E) 88º

(Fundatec) Na figura abaixo, as retas r, s e t são paralelas, e as retas p e q são transversais.

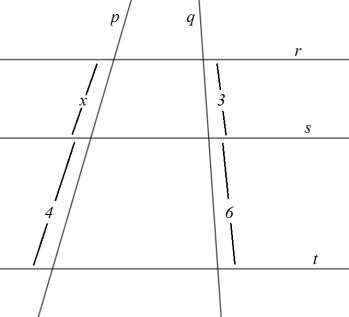
A partir das medidas indicadas na figura anterior, o valor de “x” é:

A) 2

B) 4

C) 6

D) 8

E) 10

Analise a posição relativa entre as retas a seguir:

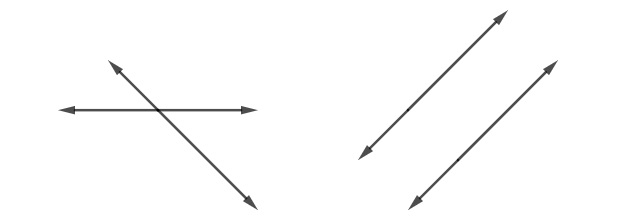
Nesse caso, as posições relativas entre as retas são, respectivamente:

A) perpendiculares e concorrentes

B) concorrentes e paralelas

C) paralelas e perpendiculares

D) concorrentes e coincidentes

E) coincidentes e paralelas

Quando duas retas paralelas são cortadas por uma reta transversal, são formados oito ângulos. Sobre a comparação desses ângulos, julgue as afirmativas a seguir:

I. Os ângulos agudos são sempre congruentes.

II. Os ângulos obtusos são sempre congruentes.

III. Um ângulo agudo é sempre complementar de um ângulo obtuso.

Marque a alternativa correta:

A) Somente a I é falsa.

B) Somente a II é falsa.

C) Somente a III é falsa.

D) Todas as afirmativas são falsas.

(BIO-RIO) As duas retas paralelas r e s da figura a seguir são cortadas por uma reta transversal t.

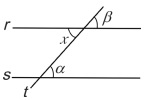
Os ângulos indicados por α, β e χ são tais que:

A) α = β = χ

B) α = β < χ

C) α > β > χ

D) α = β > χ

(Fundatec) O teorema de Tales é uma teoria aplicada na geometria acerca do conceito relacionado entre retas paralelas e transversais. O enunciado do teorema de Tales é expresso pela sentença: “a interseção entre duas retas paralelas e transversais forma segmentos proporcionais”. De acordo com esse teorema, calcule o valor de “x” na figura abaixo:

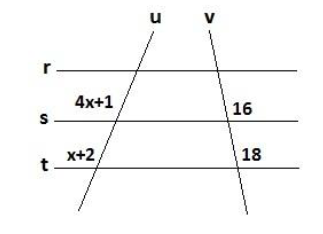
A) 0,20

B) 0,25

C) 0,30

D) 0,35

E) 0,40