Questão 1
Em uma reta numérica são colocados todos os números de determinado conjunto. Sobre ela, assinale a alternativa correta:
a) A reta numérica é uma reta comum. Entre ela e os números reais, foi criada uma correspondência biunívoca em que cada ponto está relacionado com um único número real e vice-versa.
b) A reta numérica é uma reta na qual foram colocados todos os números reais de modo que os números mais à esquerda são maiores que os números mais à direita.
c) É chamado de origem o local onde a reta numérica nasce. Sendo assim, o menor número encontrado na reta é sua origem.
d) O número zero é nulo e, por isso, não está na reta numérica.
e) Os números inteiros são colocados na reta numérica de qualquer maneira. O importante é que entre eles estejam os números decimais.
Questão 2
A respeito dos números irracionais na reta numérica, assinale a alternativa correta:
a) Os números irracionais não podem ser marcados na reta numérica, pois não há espaço para eles.
b) Os números irracionais podem ser marcados na reta numérica ao final de cada intervalo e após os números decimais.
c) Os números irracionais podem ser marcados na reta numérica, mas devem estar próximos ao zero.
d) Os números irracionais não podem ser marcados na reta numérica, pois não existe representação fracionária para eles.
e) Os números irracionais podem ser marcados na reta numérica entre os números racionais mais próximos deles.
Questão 3
Na cidade de Urupema, em determinada noite, foram registradas as seguintes temperaturas: – 1°C, – 3°C, 0°C, 3°C, 7°C e 13°C.
A variação de temperatura nessa cidade, nessa noite, foi de:
a) 13°C, pois a temperatura variou entre 0°C e 13°C.
b) 14°C, pois a temperatura variou entre – 1°C e 13°C.
c) 15°C, pois a temperatura variou entre – 1°C e 13°C.
d) 16°C, pois a temperatura variou entre – 3°C e 13°C.
e) 17°C, pois a temperatura variou entre – 3°C e 13°C.
Questão 4
Qual é a forma correta de marcar o número √2 na reta numérica?
a) Basta marcar um ponto sobre o número inteiro 2.
b) Basta calcular a raiz aproximada de 2, que é 1,41, e marcar um ponto próximo a 1,4.
c) Não existe possibilidade de marcar esse tipo de número, pois 1,41 é apenas uma aproximação. Nunca será possível encontrar o ponto exato que o representa.
d) Basta desenhar um quadrado de lado 1 com vértice na origem e fazer um círculo de raio igual à diagonal do quadrado. A intersecção desse círculo com a reta numérica é o ponto √2.
Resposta Questão 1
a) Correta.
b) Incorreta.
Quanto mais à esquerda estiver um número, menor será seu valor.
c) Incorreta.
A origem é o ponto que divide a parte negativa da parte positiva. Esse ponto é sinalizado com o número 0 (zero).
d) Incorreta.
O número zero está na reta numérica entre os números positivos e negativos.
e) Incorreta.
Os números inteiros são colocados na reta numérica de acordo com um padrão. É escolhida uma unidade de medida que dita a distância entre dois números inteiros consecutivos.
Gabarito: letra A.
Resposta Questão 2
a) Incorreta.
Os números irracionais podem, sim, ser marcados na reta numérica.
b) Incorreta.
Os números irracionais ficam distribuídos em toda a reta entre os números racionais.
Entre dois números racionais, sempre existe um número irracional e vice-versa.
c) Incorreta!
Os números irracionais ficam distribuídos em toda a extensão da reta numérica.
d) Incorreta.
Não é porque não existe representação fracionária que um número não pode ser marcado na reta numérica.
e) Correta.
Gabarito: letra E.
Resposta Questão 3
Observe a reta numérica e conte os números inteiros que vão de – 3 até 13.

Observe que de – 3 até 13 são 16 unidades. Logo, a variação foi de 16°C.
Gabarito: Letra D.
Resposta Questão 4
a) Incorreta.
O número 2 é diferente de √2. Portanto, o ponto 2 na reta numérica não representa a raiz.
b) Incorreta.
A raiz aproximada de um número oferece apenas uma aproximação de seu valor. A próxima casa da raiz de 2 é 4. Assim, 1,414 é uma aproximação melhor de √2 e deveria ser marcado um pouco à frente de 1,41. Como √2 é irracional, esse pensamento estende-se infinitamente, inviabilizando esse tipo de estratégia.
c) Incorreta.
Existe a possibilidade de marcar qualquer número real na reta numérica.
d) Correta.
A imagem a seguir ilustra essa estratégia:
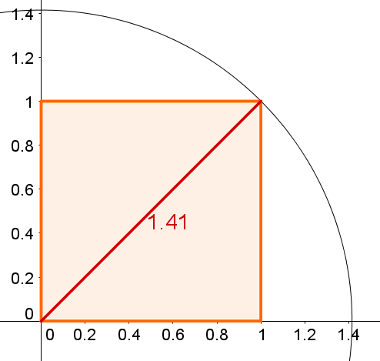
Ela é válida porque a diagonal do quadrado pode ser obtida pelo teorema de Pitágoras, em que os lados são catetos, e a diagonal é a hipotenusa. Como os lados desse quadrado medem 1, teremos:
d2 = l2 + l2
d2 = 12 + 12
d2 = 1 + 1
d = √2
A circunferência que possui o raio igual a essa diagonal obrigatoriamente passará pelo local exato do ponto √2.
Gabarito: letra D.



