Questão 1
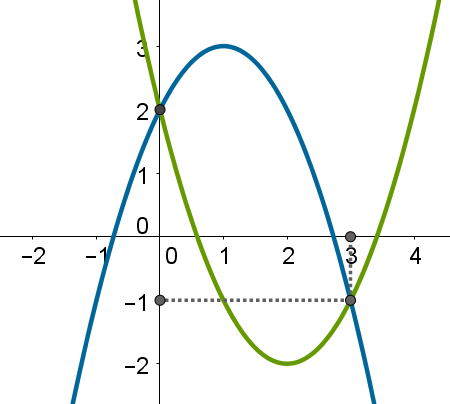
Dada a imagem a seguir com duas parábolas, assinale a alternativa correta:
a) Uma das raízes de uma das parábolas é o ponto (3, 1).
b) O valor do coeficiente c na parábola verde é diferente do valor de c na parábola azul.
c) O valor do coeficiente a é positivo em ambas as parábolas.
d) O valor do coeficiente c é 2 em ambas as parábolas.
e) Uma das raízes de uma das parábolas é o ponto (0, 2)
Questão 2
A respeito das parábolas e dos coeficientes das funções do segundo grau, assinale a alternativa correta.
a) Uma parábola que possui coeficiente C positivo não pode ter concavidade voltada para baixo.
b) Uma parábola que possui coeficiente A negativo necessariamente terá coeficiente C positivo.
c) Uma função do segundo grau com coeficiente C = 3 será representada por uma parábola que possui o ponto (3, 0).
d) Uma função do segundo grau com coeficiente C = 3 será representada por uma parábola que possui o ponto (0, 3).
e) Uma função do segundo grau com coeficiente A positivo terá ponto de máximo.
Questão 3
Os pontos conhecidos como máximo e mínimo são pontos de uma função do segundo grau que representam seu valor máximo ou mínimo. A respeito desses pontos, assinale a alternativa correta:
a) Uma função com raízes x1 e x2 possui ponto de máximo em x1 + x2.
b) Uma função com raízes em x1 e x2 possui ponto de mínimo se seu coeficiente a for negativo.
c) Uma função com raízes em x1 e x2 possui ponto de máximo caso x1 ≠ x2
d) Uma função do segundo grau não possui ponto de máximo quando não possui raízes.
e) Uma função com raízes x1 e x2 possui ponto de máximo, se a < 0, em (x1 + x2)/2
Questão 4
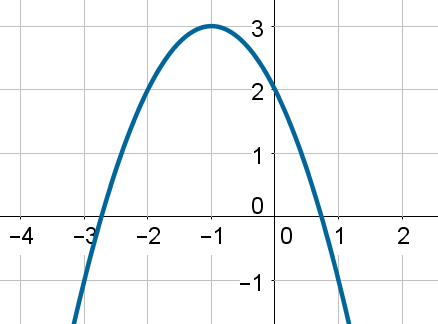
A respeito da parábola em destaque na imagem, assinale a alternativa que for correta.
a) A concavidade dessa parábola é voltada para baixo, por isso o valor do coeficiente C é negativo.
b) A concavidade dessa parábola é voltada para baixo, por isso o valor do coeficiente C é positivo.
c) O coeficiente C, nessa parábola, é igual a 3.
d) O coeficiente C, nessa parábola, é igual a 2
e) Essa parábola possui coeficiente c = 0.
Resposta Questão 1
Em uma função do segundo grau, o coeficiente a está relacionado à concavidade da parábola que a representa, e o coeficiente c é exatamente a coordenada y do ponto de encontro entre a parábola e o eixo y. Portanto, se o coeficiente c = 2, o ponto de encontro entre as parábolas e o eixo y será (0, 2), o que pode ser verificado na imagem.
Alternativa D
Resposta Questão 2
a) Incorreta!
O coeficiente C não interfere na concavidade da parábola.
b) Incorreta!
O sinal do coeficiente A não interfere na posição do coeficiente C.
c) Incorreta!
O ponto que a função possui é (0, 3).
d) Correta!
e) Incorreta!
A função que possui coeficiente A positivo possui ponto de mínimo.
Alternativa D
Resposta Questão 3
a) Incorreta!
O ponto de mínimo ou de máximo possui coordenada x igual à média aritmética das coordenadas x das raízes da função.
b) Incorreta!
Uma função possui ponto de mínimo se o coeficiente a for positivo.
c) Incorreta!
Independentemente dos valores das raízes, a função do segundo grau possui ou ponto de máximo ou ponto de mínimo.
d) Incorreta!
Uma função do segundo grau sempre possui ponto de máximo ou ponto de mínimo.
e) Correta!
Alternativa E
Resposta Questão 4
O coeficiente A de uma função do segundo grau está ligado à concavidade da parábola que o representa. Sendo assim, as alternativas a e b estão incorretas. Com relação ao coeficiente C, ele é o coeficiente y do ponto de encontro entre o eixo y e o gráfico da parábola. Como esse ponto é (0, 2), então o coeficiente C = 2.
Alternativa D