Questão 1
Durante um naufrágio, os sobreviventes dividiram a comida que lhes sobrou em partes iguais. Sabendo que a quantidade de comida duraria 9 dias para os 12 náufragos, caso fossem encontrados mais 4 sobreviventes e a comida fosse redistribuída, a quantidade de dias aproximadamente que ela duraria seria de:
A) 2 dias.
B) 4 dias.
C) 5 dias.
D) 6 dias.
E) 8 dias.
Questão 2
Na pandemia de covid-19, uma confecção se dedicou à fabricação de máscaras de tecido. Quando a confecção tinha 8 funcionários, o total de máscaras produzidas diariamente era de 184 máscaras. Com o objetivo de atingir uma produção de 500 máscaras diárias, quantos funcionários no mínimo devem ser contratados a mais?
A) 21
B) 22
C) 14
D) 15
E) 16
Questão 3
Para viajar de uma cidade para a outra, com uma velocidade média de 60 km/h, leva-se 2 horas e 30 minutos. Quanto tempo seria gasto para fazer esse mesmo percurso caso a velocidade fosse de 75 km/h?
A) 2 horas e 15 minutos
B) 2 horas
C) 1 hora e 45 minutos
D) 1 hora e 30 minutos
E) 1 hora e 15 minutos
Questão 4
Uma das bebidas mais consumidas no mundo é o refrigerante. Durante o verão, devido às altas temperaturas, o consumo dessa bebida tende a ser maior e, com isso, uma fabricante local da cidade de Juazeiro do Norte decidiu aumentar a produção da bebida. Sabendo que ele consegue produzir e engarrafar 4.000 refrigerantes em 8 horas, qual será o tempo necessário de trabalho para produzir 5.000 refrigerantes?
a) 8 horas e 30 minutos
b) 10 horas e 30 minutos
c) 9 horas
d) 9 horas e 30 minutos
e)10 horas
Questão 5
Para realizar uma reforma em larga escala em um condomínio fechado, contratou-se uma empreiteira que planejou essa reforma de acordo com a quantidade de funcionários disponíveis na empresa. Na primeira proposta, seriam necessários 15 funcionários para realizar a reforma em 10 dias, porém, durante a reunião de condomínio, decidiram que o prazo deveria ser de no máximo 6 dias para a conclusão da obra. Buscando atender à solicitação do condomínio, qual deve ser a quantidade de funcionários a mais que devem ser contratados?
A) 10
B) 12
C) 15
D) 20
E) 25
Questão 6
Uma indústria utiliza como matéria-prima principal a cana-de-açúcar em suas produções. Entre os produtos derivados da cana-de-açúcar, está o açúcar, utilizado com frequência em nossa alimentação. Com uma tonelada de cana-de-açúcar, a produção é aproximadamente 128 kg de açúcar. Qual é a quantidade de cana-de-açúcar necessária para produzir 448 kg de açúcar?
A) 2,5 toneladas
B) 2,8 toneladas
C) 3,2 toneladas
D) 3,5 toneladas
E) 4 toneladas
Questão 7
Para esvaziar totalmente uma piscina com volume de 24.000 L, com 3 ralos de mesma vazão, são necessárias cerca de 10 horas. Qual seria o tempo necessário em horas para esvaziar a piscina se ela tivesse um ralo a menos?
A) 11
B) 12
C) 13
D) 14
E) 15
Questão 8
Uma festa teve os seus detalhes planejados para que os organizadores não comprassem mais do que a quantidade necessária de comida e bebida. Sabendo que ela foi planejada para 70 pessoas e que a quantidade de salgadinhos consumidos por essas 70 pessoas é de 1.190 salgadinhos, caso 15 pessoas faltassem, qual seria a quantidade de salgadinhos consumidos?
A) 935
B) 255
C) 545
D) 600
E) 720
Questão 9
(UNA Concursos 2015) Um pintor gasta 2 galões de tinta para pintar uma parede de 45m². Responda quantos litros de tinta serão necessários para pintar 135 m², sabendo que cada galão contém 3,6L.
A) 23L
B) 19,3L
C) 28,8L
D) 21,6L
Questão 10
Uma imagem tem 2,5 cm de largura e 4,5 cm de comprimento para a confecção de um porta-retratos. Sabendo que essa imagem será ampliada de modo que o lado maior meça 18 cm e preservando as mesmas medidas, a área ocupada pela imagem vai ser de?
A) 10
B) 11
C) 12
D) 13
E) 14
Questão 11
Em uma empresa de revisão de redação, 12 corretores igualmente eficientes corrigem 1560 redações em 5 horas. Se mais 5 corretores, com a mesma eficiência, se juntarem à equipe inicial, qual será a quantidade de redações corrigidas nesse mesmo tempo?
A) 650
B) 2210
C) 2300
D) 2450
E) 3000
Questão 12
(UFES) Dois sócios, Artur e Bruno, obtiveram como lucro de um negócio o valor de R$ 7.200,00. Esse lucro foi repartido em partes proporcionais ao que cada um havia investido. Artur investiu R$ 2.400,00 e Bruno investiu R$ 1.600,00 e, por isso, ao final, Artur teve direito a um lucro maior que Bruno. A diferença entre o lucro de Artur e o lucro de Bruno foi de
A) R$ 1.200,00
B) R$ 1.360,00
C) R$ 1.400,00
D)R$ 1.440,00
E) R$ 1.500,00
Resposta Questão 1
Alternativa D.
As grandezas envolvidas são dias e quantidade de náufragos. Se eu aumento a quantidade de náufragos, sabemos que o tempo de duração da comida diminui, logo essas grandezas são inversamente proporcionais.
Montando a tabela, temos que:
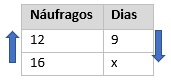
Como as grandezas são inversamente proporcionais, multiplicamos reto:
16x = 12 · 9
16x = 108
x= 108/16
x= 6,75
6 dias
Resposta Questão 2
Alternativa C.
As grandezas são quantidade de funcionários e quantidade de máscaras produzidas diariamente.
Se aumentamos o número de funcionários, o número de máscaras produzidas também aumenta, logo essas grandezas são diretamente proporcionais. Montando a tabela, temos que:
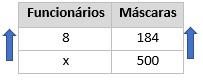
Como as grandezas são diretamente proporcionais, multiplicaremos cruzado:
184x = 500 · 8
184x = 4000
x = 4000/184
x = 21,7
Como, nesse caso, os valores decimais não fazem sentido, é necessário arredondar para mais a quantidade de funcionários, então, para produzir 500 máscaras, serão necessários 22 funcionários. Porém, queremos saber quantos funcionários a mais a empresa tem que contratar, já que ela possui 8 funcionários.
22 – 8 = 14
Resposta Questão 3
Alternativa B.
As grandezas são velocidade e tempo. Se eu aumento a velocidade, o tempo gasto diminui, então essas grandezas são inversamente proporcionais. Seja 2,5 igual a duas horas e meia, preenchendo a tabela, temos que:
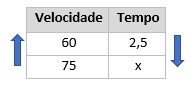
Como elas são inversamente proporcionais, multiplicamos reto:
75x = 60 · 2,5
75x = 150
x = 150/75
x =2
Resposta Questão 4
Alternativa E.
As grandezas são quantidade de refrigerantes produzidos e horas trabalhadas. Se aumentamos o tempo, consequentemente aumentamos a produção, então essas grandezas são diretamente proporcionais.
Construindo a tabela:
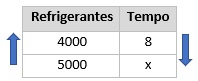
Como são grandezas diretamente proporcionais, multiplicamos cruzado.
4000x = 8 · 5000
4000x = 40000
x= 40000/4000
x = 10 horas
Resposta Questão 5
Alternativa A.
As grandezas são quantidade de funcionários e dias.
Se aumentamos a quantidade de funcionários, o prazo diminui, então essas grandezas são inversamente proporcionais. Vamos construir a tabela que representa essa situação:
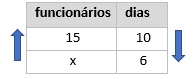
Como são grandezas inversamente proporcionais, multiplicaremos reto.
6x = 15 · 10
6x = 150
x = 150/6
x= 25.
A quantidade de funcionários a mais é 25 – 15 = 10.
Resposta Questão 6
Alternativa D.
As grandezas são quantidade de cana-de-açúcar e quantidade de açúcar. Essas grandezas são diretamente proporcionais, pois quanto mais cana-de-açúcar eu tenho, mas açúcar eu consigo produzir.

Multiplicando cruzado, temos que:
128x = 1000 · 448
128x= 448000
x = 448000/128
x= 3.500
Resposta Questão 7
Alternativa E.
As grandezas são tempo e quantidade de ralos. Como o volume é o mesmo, essa informação não é relevante para a regra de três.
Se aumentarmos a quantidade de ralos, o tempo gasto diminui, então essas grandezas são inversamente proporcionais.
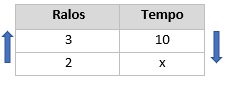
Como as grandezas são inversamente proporcionais, multiplicaremos reto:
2x = 3 · 10
2x = 30
x= 30/2
x= 15
Resposta Questão 8
Alternativa A.
As grandezas são quantidade de pessoas e quantidade de salgadinhos. Quanto mais pessoas, mais salgadinhos consumidos, logo as grandezas são diretamente proporcionais. Como 15 pessoas faltaram, então 70 – 15 = 55 pessoas presentes.
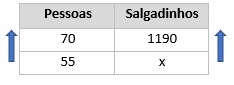
Como as grandezas são diretamente proporcionais, multiplicaremos cruzado.
70x = 1190 · 55
70x= 65.450
x=65.450/70
x= 935
Resposta Questão 9
Alternativa D.
Se cada galão tem 3,6 L, então 2 galões tem 7,2 L. Sabemos que 7,2 L pinta 45m², então as grandezas são volume de tinta e área a ser pintada. São grandezas diretamente proporcionais, pois, quanto maior a área, maior a quantidade de tinta necessária.
Montando a tabela:
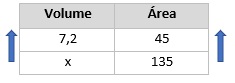
Multiplicando cruzado, temos que:
45x = 7,2 · 135
45x = 972
x= 972/45
x=21,6
Resposta Questão 10
Alternativa A.
Sabendo que uma imagem é a ampliação da outra, as grandezas são comprimento e largura. Essas grandezas são diretamente proporcionais.
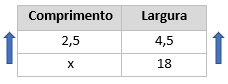
Multiplicando cruzado, temos que:
4,5x= 2,5 · 18
4,5x= 45
x=45/4,5
x=10
Resposta Questão 11
Alternativa B.
As grandezas são quantidade de corretores e quantidade de redações corrigidas. Quanto maior a quantidade de corretores, maior será a quantidade de redações corrigidas. Esse problema envolve grandezas diretamente proporcionais. Como há 5 corretores a mais, então tem um total de 12 + 5 = 17 corretores.
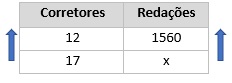
Multiplicando cruzado, temos que:
12x = 1560 · 17
12x = 26520
x=26520/12
x=2210
Resposta Questão 12
Alternativa D.
Somando os valores investidos por cada um:
1600 + 2400 = 4000
Foi investido um total de R$ 4000 reais. Sabemos que 4000 está para 7200, assim como 2400 está para o lucro de Artur. Montando a tabela, temos que:
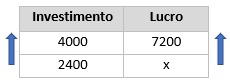
Quem investiu mais recebe mais, o que faz com que essas grandezas sejam diretamente proporcionais. Multiplicando cruzado, vamos encontrar o lucro do Artur.
4000x = 7200 · 2400
4000x = 17280000
x = 17280000/4000
x = 4320.
Se Artur lucrou 4320 reais, então Bruno teve um lucro de 7200 – 4320 = 2880. A diferença entre os lucros é de:
4320 – 2880 = 1440.



