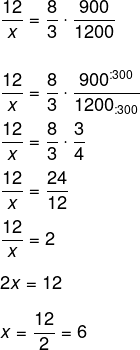Questão 1
(Enem 2015) Uma confecção possuía 36 funcionários, alcançando uma produtividade de 5400 camisetas por dia, com uma jornada de trabalho diária dos funcionários de 6 horas. Entretanto, com o lançamento da nova coleção e de uma nova campanha de marketing, o número de encomendas cresceu de forma acentuada, aumentando a demanda diária para 21.600 camisetas. Buscando atender essa nova demanda, a empresa aumentou o quadro de funcionários para 96. Ainda assim, a carga horária de trabalho necessita ser ajustada.
Qual deve ser a nova jornada de trabalho diária dos funcionários para que a empresa consiga atender a demanda?
A) 1 hora e 30 minutos
B) 2 horas e 15 minutos
C) 9 horas
D) 16 horas
E) 24 horas
Questão 2
(Nucepe) Uma construtora iniciou um empreendimento e pretendia construir durante 45 dias o maior número de casas possíveis. Os trabalhos foram iniciados com 48 operários, e, após 15 dias trabalhados, com duração de 6 horas diárias, eles perceberam que haviam construído apenas 18 casas. Vendo que não conseguiriam construir um número significativo de casas, o engenheiro responsável pela obra acrescentou 12 operários e aumentou a carga horária diária de trabalho em 2 horas. Admitindo-se que o ritmo de construção tenha se mantido constante, a quantidade de casas construídas ao final do prazo estipulado foi de
A) 42 casas.
B) 60 casas.
C) 78 casas.
D) 96 casas.
E) 114 casas.
Questão 3
(Vunesp) Cinco máquinas, todas de igual eficiência, funcionando 8 horas por dia, produzem 600 peças por dia. O número de peças que serão produzidas por 12 dessas máquinas, funcionando 10 horas por dia, durante 5 dias, será igual a
A) 1800.
B) 3600.
C) 5400.
D) 7200.
E) 9000.
Questão 4
(Enem) Uma escola lançou uma campanha para seus alunos arrecadarem, durante 30 dias, alimentos não perecíveis para doar a uma comunidade carente da região. Vinte alunos aceitaram a tarefa e, nos primeiros 10 dias, trabalharam 3 horas diárias, arrecadando 12 kg de alimentos por dia. Animados com os resultados, 30 novos alunos somaram-se ao grupo e passaram a trabalhar 4 horas por dia nos dias seguintes até o término da campanha.
Admitindo-se que o ritmo de coleta tenha se mantido constante, a quantidade de alimentos arrecadados ao final do prazo estipulado seria de:
A) 920 kg.
B) 800 kg.
C) 720 kg.
D) 600 kg.
E) 570 kg.
Questão 5
Nos processos seletivos como vestibular e concurso, é bastante comum o uso de redação como critério de avaliação dos candidatos. Uma banca examinadora aplicou uma prova, em 2012, para 3600 candidatos. Com a contratação de 6 corretores, trabalhando igualmente, foi possível corrigir todas as 3600 redações em 5 dias. Essa banca foi contratada novamente para realizar um concurso, só que, desta vez, bem maior. Sabendo que o número de inscritos desta vez é de 20.400 candidatos, qual deve ser a quantidade mínima de corretores necessária para que as redações sejam corrigidas em 10 dias?
A) 15
B) 16
C) 17
D) 18
E) 19
Questão 6
A criação de animais exige bastante cuidados, e um deles é a alimentação desses animais. Em uma fazenda especializada na criação de rebanhos de ovelhas, para alimentar 120 ovelhas, durante 12 dias, utiliza-se 792 kg de ração. Durante quanto tempo será possível alimentar um rebanho composto por 276 ovelhas com 759 kg de ração?
A) 5 dias
B) 6 dias
C) 7 dias
D) 8 dias
E) 9 dias
Questão 7
Marcela comprou 10 m² de tecido, para produzir 20 panos, com 0,5 m² cada um deles. Caso ela decida realizar a produção de 25 panos, com 12 m² de tecido, a área de cada um será de:
A) 0,38 m²
B) 0,40 m²
C) 0,42 m²
D) 0,45 m²
E) 0,48 m²
Questão 8
Para esvaziar um reservatório com 60.000 litros, 4 ralos levam 10 horas. O tempo gasto para que 7 ralos esvaziem um tanque com 120.000 litros será
A) maior que 8 horas e menor 8 horas e 30 minutos.
B) maior que 8 horas e 30 minutos e menor que 9 horas.
C) maior que 9 horas e menor que 9 horas e 30 minutos.
D) maior que 9 horas e 30 minutos e menor que 10 horas.
E) maior que 10 horas e menor que 10 horas e 30 minutos.
Questão 9
Uma indústria têxtil decidiu ampliar a sua capacidade de produção. Durante o dia, com 5 funcionários, trabalhando 6 horas por dia, essa indústria produz 800 camisetas. Qual será a quantidade de camisetas produzidas, se forem contratados mais 3 funcionários e se a jornada de trabalho for de 8 horas por dia?
A) 1700
B) 1702
C) 1704
D) 1706
E) 1708
Questão 10
Um editor de vídeo percebeu que, após sua edição, um vídeo ficou com 15 minutos, que nele foram realizados 25 cortes, e que a edição lhe exigiu 1 hora e 15 minutos de trabalho. Suponha que essas proporções sejam mantidas em um segundo vídeo. Assim, o tempo gasto nesse segundo vídeo, que, após a edição, ficou com 12 minutos e no qual foram feitos 20 cortes, será de:
A) 40 minutos
B) 48 minutos
C) 50 minutos
D) 55 minutos
E) 59 minutos
Questão 11
Durante a pandemia de covid-19, uma das medidas para se conter as contaminações foi o fechamento dos comércios não essenciais. Para atender a demanda dos seus clientes, uma empresa de consórcios passou a atendê-los via telefone e por e-mail. No atendimento, os funcionários se revesam entre responder e-mails e atender os telefonemas. Sabendo que 12 atendentes responderam, em 1 dia, o total de 114 e-mails e atenderam 180 telefonemas, o número de telefonemas atendidos, em 1 dia, por 20 funcionários, que também responderam a 76 e-mails, será de:
A) 450
B) 625
C) 710
D) 830
E) 555
Questão 12
Em uma fábrica de esmalte, 3 máquinas produzem 900 esmaltes em 12 dias. Quantos dias serão necessários para 8 máquinas produzirem 1200 esmaltes?
A) 4 dias
B) 6 dias
C) 7 dias
D) 9 dias
E) 10 dias
Resposta Questão 1
Alternativa C
Primeiro vamos identificar as grandezas, que são: quantidade de funcionários, quantidade de camisetas, e horas trabalhadas. Como nós queremos calcular as horas trabalhadas, vamos comparar essa grandeza com as demais.
Se o tempo de trabalho for maior, a quantidade de funcionários necessários será menor. (Inversamente proporcional)
Se o tempo de trabalho for maior, a quantidade de camisetas produzidas será maior. (Diretamente proporcional)
Podemos montar a tabela que descreve a situação:
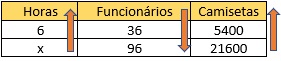
Agora, montando a equação escrevendo o inverso da fração de funcionários, temos que:

Resposta Questão 2
Alternativa C
Analisando a situação, as grandezas são: quantidade de operários, dias trabalhados, horas trabalhadas, e quantidade de casas construídas.
Note que nós queremos encontrar a quantidade de casas construídas, então, comparamos essa grandeza com as demais.
Se eu quero construir mais casas com o mesmo número de funcionários, consequentemente, a quantidade de dias e de horas trabalhadas também aumentará, então, trata-se de grandezas diretamente proporcionais.
O mesmo ocorre com a quantidade de funcionários. Se eu quero construir mais casas com o mesmo tempo, então, precisarei contratar mais funcionários. Dessa forma, todas as grandezas são diretamente proporcionais.

Montando a equação, temos que:
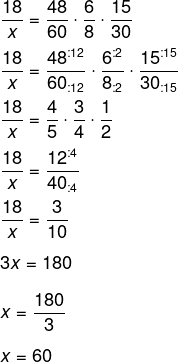
Assim, o total de casas construídas será igual a 60 + 18 = 78.
Resposta Questão 3
Alternativa E
As grandezas são: quantidade de peças, quantidade de máquinas, horas, e dias.
Comparando a quantidade de peças com as demais grandezas, se aumentarmos a quantidade de peças produzidas sem mexer no número de máquinas, o tempo (horas e dias) necessário também será maior.
Comparando a quantidade de peças com a quantidade de máquinas, se eu preciso produzir mais peças, então, serão necessárias mais máquinas. Todas as grandezas são diretamente proporcionais.

Resolvendo a equação:
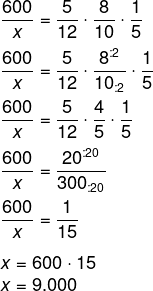
Resposta Questão 4
Alternativa A
As grandezas são: quantidade de alunos, quantidade de alimentos, horas, e dias.
Queremos encontrar a quantidade de alimentos, então, vamos comparar essa grandeza com as demais.
Se aumentamos a quantidade de alimentos para serem arrecadados, serão necessários mais alunos e também mais horas e dias, logo, as grandezas são diretamente proporcionais.
Montando a tabela, temos que:

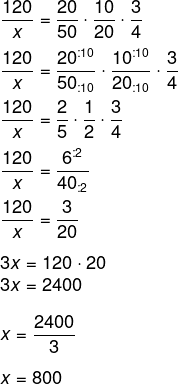
Sabemos que já foram coletados 120 kg, inicialmente, então temos que 800 + 120 = 920.
Resposta Questão 5
Alternativa C
As gradezas são: quantidade de corretores, dias, quantidade de redações. Queremos encontrar a quantidade de corretores necessária, então, vamos comparar essa grandeza com as demais.
Ao comparar a quantidade de corretores com o tempo, se eu aumento a quantidade de corretores, o tempo necessário para corrigir será menor.
Ao comparar quantidade de corretores com quantidade de redações corrigidas, se aumentamos a quantidade de corretores, consequentemente, a quantidade de redações corrigidas será maior.
Agora, vamos montar a tabela:
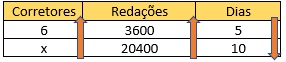
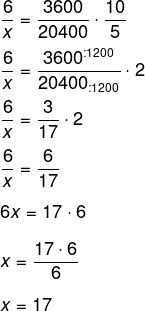
Resposta Questão 6
Alternativa A
As grandezas são: quantidade de ovelhas, quantidade de ração e quantidade de dias. Queremos encontrar o tempo de duração do alimento, então, vamos comparar essa grandeza com as demais.
Para que o alimento dure mais dias, será necessário que haja menos ovelhas, logo, essas grandezas são inversamente proporcionais.
Para que o alimento dure mais dias, será necessário que haja mais ração, logo, essas grandezas são diretamente proporcionais.
Montando a tabela:
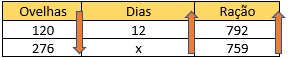
Agora, resolveremos a equação, isolando a grandeza da incógnita e invertendo a razão das ovelhas:
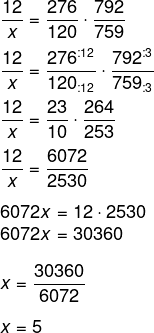
Resposta Questão 7
Alternativa E
As grandezas são: área do tecido, quantidade de panos e área de cada pano. Queremos encontrar a área de cada pano, então, vamos comparar essa grandeza com as demais.
Comparando a área do tecido com a área do pano, se eu aumento a área de cada pano, a área do tecido será maior, logo, essas grandezas são diretamente proporcionais.
Agora, comparando a quantidade de panos com a área de cada um deles, se a área dos panos for maior, a quantidade que eu consigo produzir deles será menor, logo, essas grandezas são inversamente proporcionais.

Resolvendo a equação, temos que:
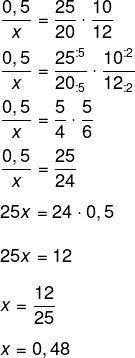
Resposta Questão 8
Alternativa B
As grandezas são: volume, quantidade de ralos, e tempo.
Queremos encontrar o valor da grandeza tempo, então, comparamos essa grandeza com as demais.
Se o volume aumenta, consequentemente, o tempo para esvaziar o reservatório será maior, logo, essas grandezas são diretamente proporcionais.
Se a quantidade de ralos diminui, o tempo para esvaziar o reservatório será maior, logo, essas grandezas são inversamente proporcionais.
Montando a tabela, temos que:

Resolvendo a equação, temos que:
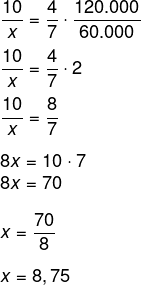
Entre 8 horas e 30 minutos e 9 horas.
Resposta Questão 9
Alternativa D
As grandezas são: quantidade de funcionários, tempo, e quantidade de camisetas produzidas.
Queremos saber a quantidade de camisetas produzidas, logo, vamos comparar essa grandeza com as demais.
Se aumentarmos a quantidade de camisetas produzidas em um mesmo tempo, consequentemente, precisaremos de mais funcionários, logo, essas grandezas são diretamente proporcionais.
Se aumentarmos a quantidade de camisetas produzidas para uma mesma quantidade de funcionários, o tempo gasto será maior, logo, essas grandezas também são diretamente proporcionais.
Montando a tabela, temos que:

Agora, basta resolver a equação:
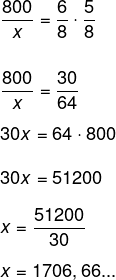
Nesse caso, é necessário arredondar para menos, já que o tempo não será o suficiente para confeccionar a última camiseta, então, teremos 1706 camisetas produzidas.
Resposta Questão 10
Alternativa B
As grandezas são: quantidade de cortes nos vídeos, tempo de edição e tempo de gravação.
Se há mais tempo de vídeo e mais cortes a serem feitos, o tempo gasto para editar será maior, consequentemente, essas grandezas são diretamente proporcionais. Transformando 1 hora e 15 minutos em minutos, teremos 75 minutos, logo, é possível montar a tabela:
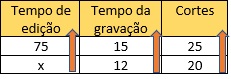
Resolvendo a equação:
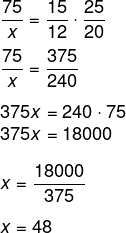
O tempo gasto será de 48 minutos.
Resposta Questão 11
Alternativa A
As grandezas são: quantidade de atendentes, quantidade de ligações e quantidade e-mails.
Queremos encontrar a quantidade de telefonemas atendidos, então, vamos comparar essa grandeza com as demais.
Se eu aumento o número de telefonemas atendidos, eu precisarei de mais funcionários. Essas grandezas são diretamente proporcionais.
Se, com o mesmo número de funcionários, eu preciso de mais telefonemas atendidos, o número de e-mail respondidos será menor, logo, essas grandezas são inversamente proporcionais.
Montando a tabela:
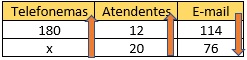
Agora basta resolver a equação:
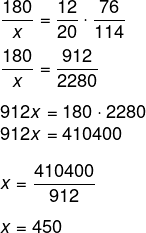
Resposta Questão 12
Alternativa B
As grandezas são: quantidade de máquinas, quantidade de esmalte, e dias. A incógnita está na grandeza tempo, então, vamos analisar a proporção entre ela e as demais.
Tempo e máquinas são inversamente proporcionais, pois, se eu aumentar o tempo, a quantidade de máquinas necessárias para realizar uma mesma produção será menor.
Tempo e quantidade de esmalte são grandezas diretamente proporcionais, pois, se eu aumento o tempo, a quantidade de esmalte produzidos também será maior.
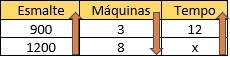
Montando as razões, vamos inverter a razão das máquinas, então, temos que: