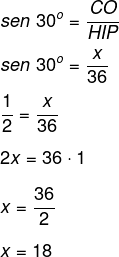Questão 1
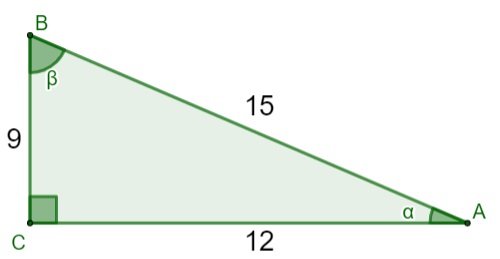
Analisando o triângulo retângulo, com suas medidas dadas em centímetros, podemos afirmar que o valor do seno do ângulo ꞵ é igual a:
A) 3/5
B) 4/5
C) 5/4
D) 4/3
E) 3/4
Questão 2
Um engenheiro foi contratado para calcular a altura de um prédio sem subir nele. A uma distância de 40 metros, constatou-se que era possível construir o seguinte triângulo retângulo:

Podemos afirmar que a altura do prédio é de, aproximadamente:
(Dados: use √3 = 1,7)
A) 20 m
B) 21,5 m
C) 22,7 m
D) 23 m
E) 23,8 m
Questão 3
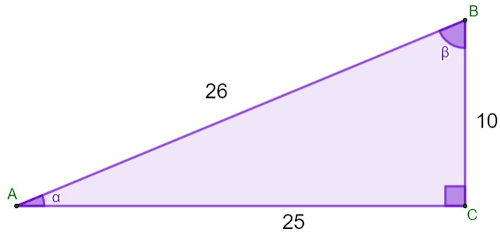
No triângulo retângulo a seguir, sabendo que seus lados estão medidos em metros, o valor do cosseno do ângulo ɑ é:
A) 0,96
B) 0,38
C) 0,40
D) 1,04
E) 2,60
Questão 4
Qual deve ser o valor do seno de um ângulo, sabendo que ele se encontra no primeiro quadrante e que o cosseno desse mesmo ângulo é igual a 3/5.
A) 4/5
B) 2/5
C) 3/4
D) 1/5
E) 2/3
Questão 5
Um avião levantou voo, formando um ângulo de 20º com o solo, e atingiu uma altura de 1368 metros. A distância percorrida pelo avião, em metros quadrados, foi de:
(Use: sen 20º = 0,342; cos 20º = 0,94; tg 20º = 0,364)
A) 2 km
B) 3 km
C) 4 km
D) 5 km
E) 6 km
Questão 6
Um terreno possui o formato de um retângulo cuja base mede 8 cm, sabendo que o ângulo formado entre a base e a diagonal é de 30º, qual o valor que mais se aproxima da diagonal? (Use √3 = 1,7)
A) 5
B) 6
C) 7
D) 8
E) 9
Questão 7
O valor do comprimento base de um triângulo retângulo isósceles em que os lados adjacentes à base medem 6√2 cm é:
A) 15 cm
B) 12 cm
C) 10 cm
D) 8 cm
E) 6 cm
Questão 8
Uma tirolesa será feita em uma montanha que possui 100 metros de altura. Sabendo que ela será amarrada de tal modo que forme com o chão um ângulo de 30º, qual deve ser o tamanho do cabo da tirolesa?
A) 100 m
B) 125 m
C) 150 m
D) 175 m
E) 200 m
Questão 9
As torres Puerta de Europa, construídas numa avenida de Madri, na Espanha, são inclinadas uma contra a outra. A inclinação das torres é de 15° com a vertical, e elas têm, cada uma, altura de 114 m (a altura é indicada na figura como o segmento AB). Essas torres são um bom exemplo de um prisma oblíquo de base quadrada, e uma delas pode ser observada na imagem.

Utilizando 0,26 como valor aproximado para a tangente de 15° e duas casas decimais nas operações, descobre-se que a área da base desse prédio ocupa na avenida um espaço
A) menor que 100 m².
B) entre 100 m² e 300 m².
C) entre 300 m² e 500 m².
D) entre 500 m² e 700 m².
E) maior que 700 m².
Questão 10
(Enem) Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular de 3 km x 2 km que contém uma área de extração de ouro delimitada por um quarto de círculo de raio 1 km a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro, os irmãos acordaram em repartir a propriedade de modo que cada um ficasse com a terça parte da área de extração, conforme mostra a figura.
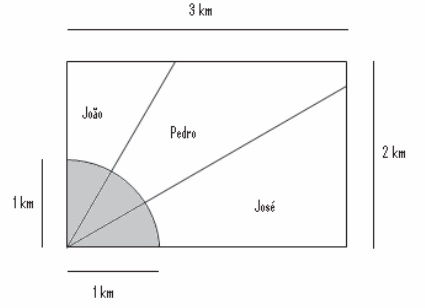
Em relação à partilha proposta, constata-se que a porcentagem da área do terreno que coube a João corresponde, aproximadamente, a:
(Considere √3/3 = 0,58)
A) 50%
B) 43%
C) 37%
D) 33%
E) 19%
Questão 11
(Cesgranrio) Uma escada de 2 m de comprimento está apoiada no chão e em uma parede vertical. Se a escada faz 30° com a horizontal, a distância do topo da escada ao chão é de:
A) 0,5 m
B) 1 m
C) 1,5 m
D) 1,7 m
E) 2 m
Questão 12
(Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira, eleva-se verticalmente de:
A) 6√3 m.
B) 12 m.
C) 13,6 m.
D) 9√3 m.
E) 18 m.
Resposta Questão 1
Alternativa B
Sabemos que o seno é a razão entre o cateto oposto ao ângulo e a hipotenusa. Analisando a imagem, sabemos que o cateto oposto ao ângulo ꞵ mede 12 e a hipotenusa mede 15, então, temos que:
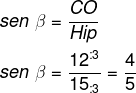
Resposta Questão 2
Alternativa C
Analisando a imagem, podemos construir o seguinte triângulo retângulo:
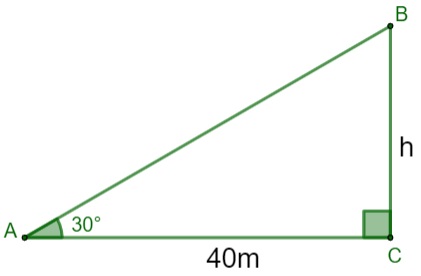
Para encontrar o valor de h, que é cateto oposto ao ângulo de que conhecemos o valor, utilizaremos a tangente, pois queremos o cateto oposto e conhecemos o cateto adjacente. Consultando a tabela, é possível encontrar o valor da tangente, então temos que:
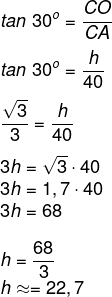
Resposta Questão 3
Alternativa A
Analisando o ângulo ɑ, sabemos que o cosseno dele é o cateto adjacente, que mede 25 m, dividido pela hipotenusa, que mede 26 m.
![]()
Resposta Questão 4
Alternativa A
Utilizando a relação fundamental da trigonometria, temos que:
sen²x + cos²x = 1
Então, substituindo o valor do cosseno, basta resolver a equação:
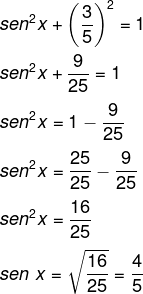
Resposta Questão 5
Alternativa C
Primeiro construiremos a imagem que representa a situação:
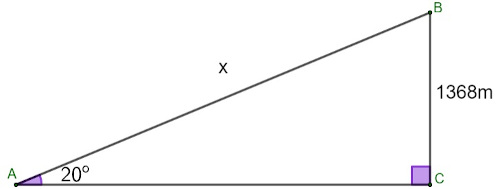
A razão trigonométrica que relaciona cateto oposto e hipotenusa é o seno, então, temos que:
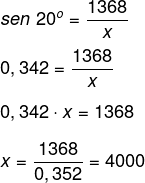
x = 4 km
Resposta Questão 6
Alternativa E
Sabemos que a diagonal divide o ângulo, formando um ângulo de 30º com a base, vamos representar essa situação:
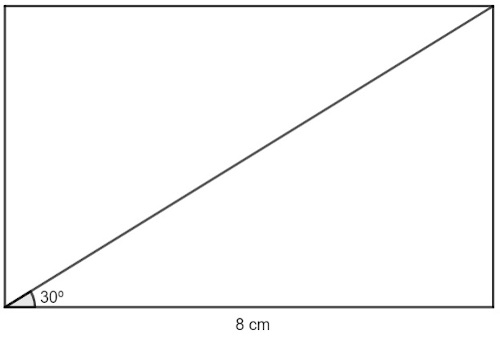
Seja x a diagonal, calculando o cos x, temos que:
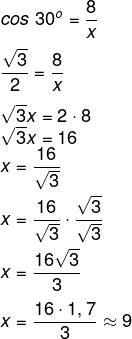
Resposta Questão 7
Alternativa B
Primeiro faremos o esboço do triângulo. Como ele é retângulo, um dos seus ângulos é igual a 90º, como a soma dos três ângulos é igual a 180º e o triângulo também é isósceles, então os ângulos da base medem 45º.
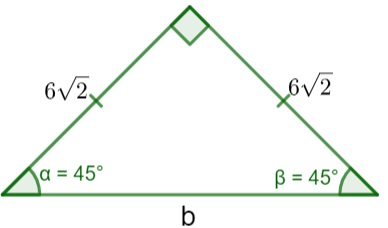
Como queremos encontrar o valor de b, nesse caso, tanto faz entre calcular o seno ou o cosseno de dos ângulos:
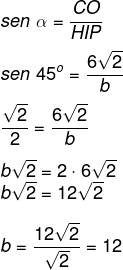
Resposta Questão 8
Alternativa E
Sabemos que a altura é igual a 100 metros e que é oposta ao ângulo de 30º, então, utilizaremos seno de 30º para encontrar a hipotenusa.
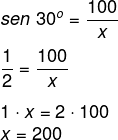
Resposta Questão 9
Alternativa E
O seguimento AB divide o prédio em dois triângulos retângulos, sabendo que o ângulo B é igual a 15º e que conhecemos o cateto adjacente a ele, é possível calcular o tamanho da base utilizando a tangente.
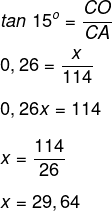
Como a base é um quadrado, sua área será 29,64² = 878,53.
Resposta Questão 10
Alternativa E
Para encontrar a área do terreno do João, sabemos que o ângulo reto foi dividido em 3 partes iguais, logo, o ângulo representado pela região de extração de ouro é de 30º. Conhecemos a altura de 2 km do terreno, então, vamos calcular o cateto oposto ao ângulo utilizando a tangente.
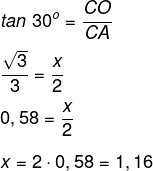
A área do João, Aj, é dada pelo produto entre a base e a altura dividido por dois, e a área do retângulo At é dada pelo produto entre a base e a altura. Para calcular a porcentagem, basta calcular a razão entre Aj e At.
At = 2 · 3 = 6
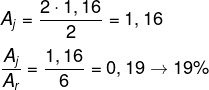
Resposta Questão 11
Alternativa B
Analisando a situação, podemos representá-la por um triângulo retângulo, em que a sua hipotenusa vale 2 m, conforme a imagem a seguir:
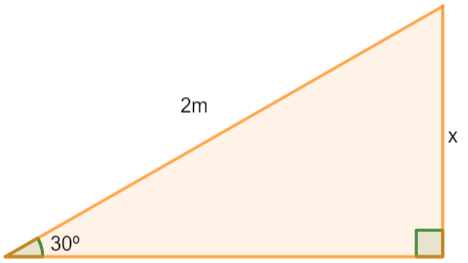
Aplicando o seno, é possível encontrar o valor de x:
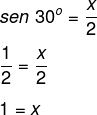
Resposta Questão 12
Alternativa E
Para resolver a situação, construiremos o triângulo retângulo:
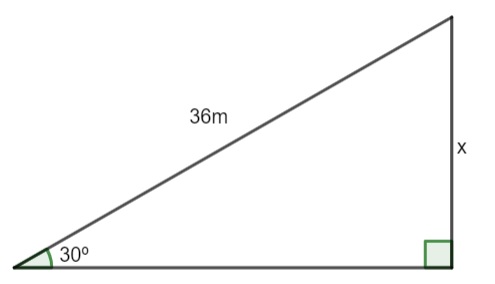
A altura da rampa, na imagem representada por x, é o cateto oposto ao ângulo de 30º. A razão que utiliza cateto oposto e hipotenusa é o seno. Então, temos que: