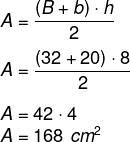Questão 1
Qual é a área de um trapézio isósceles que possui base maior medindo 32 cm, base menor medindo 20 cm e altura igual a 8 cm?
A) 168 cm².
B) 165 cm².
C) 160 cm².
D) 156 cm².
E) 150 cm².
Questão 2
Considerando que um quadrado possui a mesma área de um retângulo cujas medidas dos lados são 75 cm e 48 cm, o perímetro desse quadrado é de
A) 200 cm².
B) 240 cm².
C) 270 cm².
D) 300 cm².
Questão 3
Dentre as alternativas a seguir, não se configura como quadrilátero o
A) quadrado.
B) trapézio.
C) paralelogramo.
D) paralelepípedo.
E) losango.
Questão 4
Um losango possui uma diagonal medindo 1,25x e a diagonal menor medindo x. Se a área desse losango é igual a 80 cm, a sua diagonal maior, em centímetros, é igual a
A) 12.
B) 13.
C) 14.
D) 15.
E) 16.
Questão 5
Analisando o paralelogramo a seguir, sabendo que a medida de seus lados está dada em centímetros, podemos afirmar que o valor do seu perímetro é de
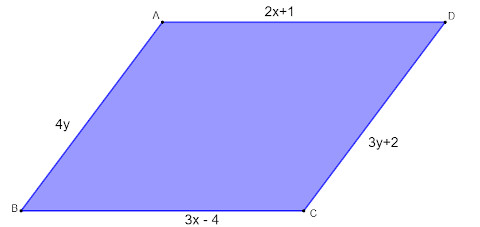
A) 34 cm.
B) 35 cm.
C) 37 cm.
D) 38 cm.
E) 40 cm.
Questão 6
A imagem a seguir representa a área a ser plantada na fazenda do Seu Joaquim.
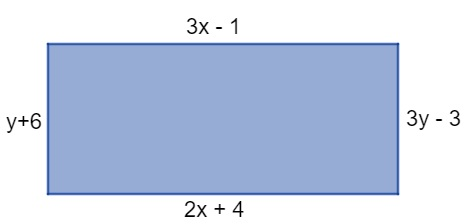
Analisando esse terreno, sendo a medida dos lados dada em metros, calcula-se que a área a ser plantada é igual a
A) 125 m².
B) 127 m².
C) 132 m².
D) 135 m².
E) 147 m².
Questão 7
No intuito de fazer uma plantação em um terreno, foi separada uma área no formato de um losango, com as medidas dadas em metros, conforme a imagem a seguir:
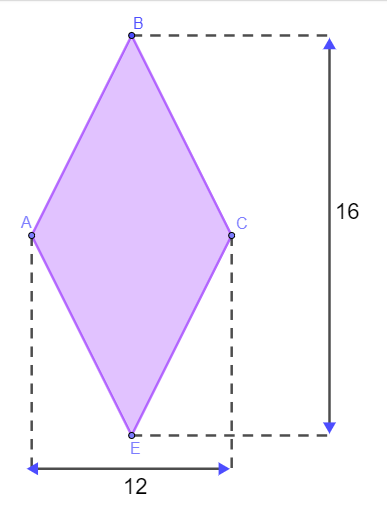
Para evitar perdas no plantio causadas por animais, o dono do terreno decidiu cercá-lo com arame farpado, completando 4 voltas em torno da área. Supondo que seja possível comprar exatamente o tamanho necessário para cercar o terreno dessa maneira, a quantidade de arame farpado necessária é igual a
A) 100 m.
B) 120 m.
C) 360 m.
D) 400 m.
E) 480 m.
Questão 8
Qual é a área de um losango que possui diagonal maior igual a 15 cm e diagonal menor igual a 1/3 da diagonal maior?
A) 37,5 cm².
B) 35 cm².
C) 32,5 cm².
D) 30 cm².
E) 28,5 cm².
Questão 9
(IFG 2018) Na fase final da construção de um ginásio, um pedreiro necessita ladrilhar o chão que representa uma base retangular, cujas dimensões são 18 metros e 32 metros. Os ladrilhos utilizados são quadrados com 24 centímetros de lado. O número de ladrilhos necessários para revestir o espaço é de
A) 100.000.
B) 10.000.
C) 1.000.
D) 100.
Questão 10
(IFG 2012) Em um retângulo, a razão entre a medida da altura e a medida da base é de 2/5, e o perímetro desse retângulo mede 42 cm. A área desse retângulo em cm² é igual a
A) 88.
B) 90.
C) 91.
D) 94.
E) 96.
Questão 11
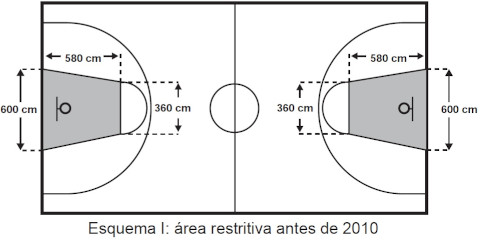
(Enem 2015) O Esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas.
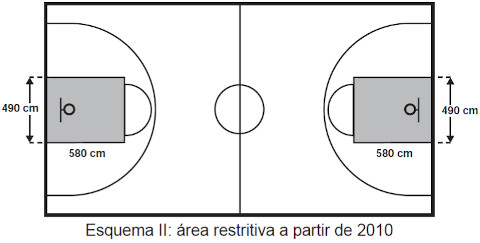
Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.
Após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)
A) aumento de 5800 cm².
B) aumento de 75400 cm².
C) aumento de 214600 cm².
D) diminuição de 63800 cm².
E) diminuição de 272600 cm.
Questão 12
Sobre os quadriláteros, julgue as afirmativas a seguir:
I → O quadrado é também um losango e um retângulo.
II → O losango sempre possui lados congruentes.
III → Um trapézio é um caso de paralelogramo.
Marque a alternativa correta:
A) Somente a alternativa I é falsa.
B) Somente a alternativa II é falsa.
C) Somente a alternativa III é falsa.
D) Todas as afirmativas são verdadeiras.
Resposta Questão 2
Alternativa B
A área do retângulo é calculada por:
A = b · h
A = 75 · 48
A = 3600 cm²
Sabemos que o quadrado possui a mesma área que o retângulo e que a área do quadrado é l²:
l² = 3600
l = √3600
l = 60 cm
Então, o perímetro desse quadrado é igual a:
4l = 4 ⸳ 60 = 240 cm²
Resposta Questão 4
Alternativa E
A área do losango é calculada por:
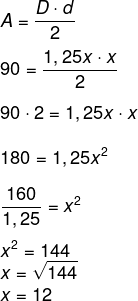
Como x = 12, a diagonal maior é igual a 12 ⸳1,25 = 16 cm
Resposta Questão 5
Alternativa D
Sabe-se que os lados opostos são congruentes. Portanto, para encontrar o valor de y, calcula-se:
4y = 3y + 2
4y – 3y = 2
y = 2
Agora, para encontrar o valor de x:
3x – 4 = 2x + 1
3x – 2x = 1 + 4
x = 5
Logo, os lados medem:
4y = 4 ⸳ 2 = 8
3x – 4 = 3 · 5 – 4 = 15 – 4 = 11
Sendo assim, o perímetro é igual a:
P = 2 (8 + 11)
P = 2 · 19
P = 38 cm
Resposta Questão 6
Alternativa E
Em um retângulo, os lados opostos são congruentes. Portanto, igualaremos as equações que estão em lados opostos.
Analisando os lados horizontais, tem-se o seguinte:
3x – 1 = 2x + 4
3x – 2x = 4 + 1
x = 5
Agora, pelos lados verticais, temos que:
3y – 3 = y + 6
3y – y = 6 + 3
2y = 9
y = 9/2
y = 4,5
Para encontrar a medida dos lados do retângulo, substituiremos os valores encontrados:
3x – 1 com x = 5
3 ⸳ 5 – 1 = 15 – 1 = 14
y + 6 com y = 4,5
4,5 + 6 = 10,5
Para encontrar o valor da área, basta multiplicar as medidas dos dois lados:
A = 10,5 ⸳ 14 = 147 m²
Resposta Questão 7
Alternativa E
Para encontrar o valor do lado do losango, primeiramente calcularemos a metade do comprimento de cada uma das diagonais:
D = 16 → D/2 = 8
d = 12 → d/2 = 6
Considerando que:
l² = 8² + 6²
l² = 64 + 36
l² = 100
l = √100
l = 10 m
Agora é possível calcular seu perímetro:
P = 4l
P = 4 · 30
P = 120 metros
Como deseja-se dar 4 voltas, calcularemos:
120 ⸳ 4 = 480 m
Resposta Questão 8
Alternativa A
Se a diagonal menor equivale a 1/3 da maior, então d = 15 : 3 = 5
Logo, a área do losango será
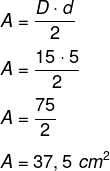
Resposta Questão 9
Alternativa B
Como a medida da cerâmica está em centímetros, para realizar a comparação entre a área do ginásio e a área dos ladrilhos, calcularemos a área do ginásio também em centímetros:
18 m → 1800 cm
32 m → 3200 cm
Ag = 1800 · 3200
Ag = 5.760.000
Al = 24 · 24 = 576
Realizando a divisão:
5.760.000 : 575 = 10.000
Resposta Questão 10
Alternativa B
Sendo 2x a altura e 5x a base, temos que:
P = 2 (2x + 5x) = 42
4x + 10x = 42
14x = 42
x = 42/14
x = 3
Então, os lados medem:
2x = 2 · 3 = 6
5x = 5 · 3 = 15
Agora basta calcular a sua área:
A = 6 · 15 = 90
Resposta Questão 11
Alternativa A
De início, calcularemos a área dos garrafões.
No Esquema I, o garrafão é um trapézio, com bases medindo 600 cm e 380 cm e altura medindo 580 cm. A área do trapézio é calculada por:
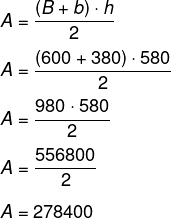
No Esquema II, o garrafão é um retângulo de base de 580 cm e altura de 490 cm.
A = b · h
A = 580 · 490
A= 284200
Calculando a diferença entre as áreas, é possível perceber que houve diminuição:
284200 – 278400 = 5800 cm²
Resposta Questão 12
Alternativa C
I → Verdadeira
O quadrado possui todos os lados congruentes, logo, ele é um losango. Além disso, ele possui todos os ângulos retos, o que faz com que ele seja um retângulo.
II → Verdadeira
Por definição, o losango é um quadrilátero que possui todos os lados congruentes.
III → Falsa
O trapézio não possui todos os lados paralelos.