Questão 1
Sabendo que os números 2, 6 e x são diretamente proporcionais aos números y, 9 e 13,5, o produto x : y é:
A) 2
B) 3
C) 4
D) 5
E) 6
Questão 2
Quando Thiago foi ao supermercado, ele decidiu observar a relação entre as grandezas. Thiago percebeu que quando ele realizava a pesagem de uma determinada fruta, existia uma relação de proporcionalidade entre o peso da fruta e o valor pago, pois:
A) o peso e o valor pago são grandezas inversamente proporcionais.
B) o peso e o valor pago são grandezas diretamente proporcionais.
C) o peso e o valor pago são grandezas que se relacionam sem proporção.
D) o peso e o valor pago são grandezas relativamente proporcionais.
Questão 3
Determinada substância possui massa igual a 300 g e volume igual 450 cm³. Caso quisermos obter 1 kg dessa substância, é necessário um volume igual a:
A) 900 cm³
B) 1050 cm³
C) 1200 cm³
D) 1350 cm³
E) 1500 cm³
Questão 4
Uma gráfica recebeu um pedido para realizar a produção de apostilas de uma rede de ensino. O estabelecimento possui 4 máquinas, e foi estimado que elas levariam 12 horas para fazer o serviço. Caso houvesse 2 máquinas a mais, o tempo necessário para atender a essa demanda seria de:
A) 6 horas
B) 6 horas e 30 minutos
C) 7 horas
D) 7 horas e 30 minutos
E) 8 horas
Questão 5
Marcela foi a um restaurante e pagou R$ 37,50 por 750 gramas de comida. Já Rogério pagou R$ 45,00 pelo seu prato, mas acabou não reparando na quantidade de comida que ele colocou. A quantidade de comida que Rogério colocou foi de:
A) 800 gramas
B) 850 gramas
C) 900 gramas
D) 950 gramas
E) 1000 gramas
Questão 6
Na criação de um negócio, havia 2 sócios. Um deles investiu R$ 150.000,00, e o outro, R$ 250.000,00. Ao final do primeiro ano, a empresa obteve um lucro de R$ 1.200.000,00, e o valor foi dividido de forma diretamente proporcional ao valor investido por cada um deles. A quantia recebida pelo sócio que investiu mais foi de:
A) R$ 750.000,00
B) R$ 800.000,00
C) R$ 850.000,00
D) R$ 900.000,00
E) R$ 950.000,00
Questão 7
(Enem 2020) Um motociclista planeja realizar uma viagem cujo destino fica a 500 km de sua casa. Sua moto consome 5 litros de gasolina para cada 100 km rodados, e o tanque da moto tem capacidade para 22 litros. Pelo mapa, observou que no trajeto da viagem o último posto disponível para reabastecimento, chamado Estrela, fica a 80 km do seu destino. Ele pretende partir com o tanque da moto cheio e planeja fazer somente duas paradas para reabastecimento, uma na ida e outra na volta, ambas no posto Estrela. No reabastecimento para a viagem de ida, deve considerar também combustível suficiente para se deslocar por 200 km no seu destino. A quantidade mínima de combustível, em litro, que esse motociclista deve reabastecer no posto Estrela na viagem de ida, que seja suficiente para fazer o segundo reabastecimento, é:
A) 13
B) 14
C) 17
D) 18
E) 21
Questão 8
(Enem 2015) Um pesquisador, ao explorar uma floresta, fotografou uma caneta de 16,8 cm de comprimento ao lado de uma pegada. O comprimento da caneta (c), a largura (L) e o comprimento (C) da pegada, na fotografia, estão indicados no esquema:
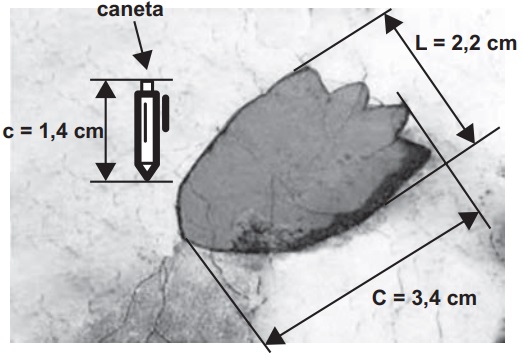
A largura e o comprimento reais da pegada, em centímetros, são, respectivamente, iguais a
A) 4,9 e 7,6.
B) 8,6 e 9,8.
C) 14,2 e 15,4.
D) 26,4 e 40,8.
E) 27,5 e 42,5.
Questão 9
(Enem 2009) A suspeita de que haveria uma relação causal entre tabagismo e câncer de pulmão foi levantada pela primeira vez por meio de observações clínicas. Para testar essa possível associação, foram conduzidos inúmeros estudos epidemiológicos. Dentre esses, houve o estudo do número de casos de câncer em relação ao número de cigarros consumidos por dia, cujos resultados são mostrados no gráfico a seguir. De acordo com as informações do gráfico,
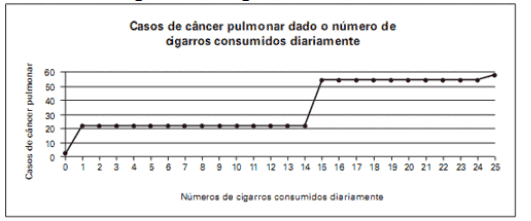
A) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas inversamente proporcionais.
B) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas que não se relacionam.
C) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas diretamente proporcionais.
D) uma pessoa não fumante certamente nunca será diagnosticada com câncer de pulmão.
E) o consumo diário de cigarros e o número de casos de câncer de pulmão são grandezas que estão relacionadas, mas sem proporcionalidade.
Questão 10
Uma herança de R$ 800.000,00 foi dividida de forma diretamente proporcional às idades de 5 filhos. Sabendo que os filhos tinham respectivamente 43, 42, 30, 24 e 21 anos, o filho que obteve o maior valor da herança recebeu o total de:
A) R$ 210.000,00
B) R$ 215.000,00
C) R$ 220.000,00
D) R$ 235.000,00
E) R$ 250.000,00
Questão 11
Os ângulos internos de um triângulo são diretamente proporcionais aos números 2, 3 e 4. Assim, o valor do menor ângulo desse triângulo é:
A) 20°
B) 30°
C) 40°
D) 60°
E) 80°
Questão 12
(Enem 2021) Em uma corrida automobilística, os carros podem fazer paradas nos boxes para efetuar trocas de pneus. Nessas trocas, o trabalho é feito por um grupo de três pessoas em cada pneu. Considere que os grupos iniciam o trabalho no mesmo instante, trabalham à mesma velocidade e cada grupo trabalha em um único pneu. Com os quatro grupos completos, são necessários 4 segundos para que a troca seja efetuada. O tempo gasto por um grupo para trocar um pneu é inversamente proporcional ao número de pessoas trabalhando nele. Em uma dessas paradas, um dos trabalhadores passou mal, não pôde participar da troca e nem foi substituído, de forma que um dos quatro grupos de troca ficou reduzido. Nessa parada específica, com um dos grupos reduzido, qual foi o tempo gasto, em segundo, para trocar os quatro pneus?
A) 6,0
B) 5,7
C) 5,0
D) 4,5
E) 4,4
Resposta Questão 1
Alternativa B
Como os números são diretamente proporcionais:
\(\frac{2}{y}=\frac{6}{9}=\frac{x}{13,5}\)
Das primeiras frações, temos que:
\(\frac{2}{y}=\frac{6}{9}\)
\(6y=2\cdot9\)
\(6y=18\)
\(y=\frac{18}{6}\)
\(y=\ 3\)
Calculando o valor de x:
\(\frac{6}{9}=\frac{x}{13,5}\)
\(9x=6\cdot13,5\)
\(9x=81\)
\(x=\frac{81}{9}\)
\(x=9\)
Por fim, calculando o valor de x : y:
9 : 3 = 3
Resposta Questão 2
Alternativa B
A massa e valor pago são grandezas diretamente proporcionais, pois à medida que o peso aumenta, o valor também aumenta na mesma proporção.
Resposta Questão 3
Alternativa E
Considerando x o valor do volume e tendo em mente que massa e volume são proporcionais, podemos fazer uma regra de três:
\(\frac{300}{450}=\frac{1000}{x}\)
\(300x=1000\cdot450\)
\(300x=450000\)
\(x=\frac{450000}{300}\)
\(x=1500\)
Portanto, o volume necessário é de 1500 cm³.
Resposta Questão 4
Alternativa E
Sabemos que 4 máquinas correspondem a 12 horas. Assim, com duas máquinas as mais haverá 6 máquinas que levarão x horas para completar a tarefa. Sabemos que 6 máquinas levam menos tempo do que 4 máquinas, logo tempo e quantidade de máquinas são grandezas inversamente proporcionais. Então, temos que:
\(\frac{4}{6}=\frac{x}{12}\)
\(6x=4\cdot12\)
\(6x=48\ \)
\(x=\frac{48}{8}\)
\(x=8\ horas\)
Resposta Questão 5
Alternativa C
Sabemos que o preço é proporcional à quantidade de alimento em gramas. Logo:
\(\frac{37,5}{750}=\frac{45}{x}\)
\(37,5x=45\cdot750\)
\(37,5x=33750\)
\(x=\frac{33750}{37,5}\)
\(x=900\)
Resposta Questão 6
Alternativa A
Como o lucro foi proporcional ao valor do investimento, sabemos que:
\(150.000k+250.000k=1.200.000\)
\(400.000k=1.200.000\)
\(k=1.200.000\ \ 400.000\)
\(k=3\)
O sócio que mais investiu fez a aplicação de 250.000k:
\(250.000\cdot3=750.000\)
Resposta Questão 7
Alternativa C
Primeiramente, calcularemos o consumo em 420 km:
\(\frac{420}{100}=\frac{x}{5}\)
\(100x=420\cdot5\)
\(100x=2100\)
\(x=\frac{2100}{100}\)
\(x=21\ L\)
Com o tanque cheio, cabem 22 L, logo sobra 1 L.
O consumo desse veículo em 80 km pode ser calculado por:
\(\frac{80}{100}=\frac{y}{5}\)
\(100y=80\cdot5\)
\(100y=400\)
\(y=\frac{400}{100}\)
\(y=4\ L\)
Sabemos que em 100 km ele consome 5 litros. Logo, em 200 km ele consumirá o dobro, ou seja, 10 litros.
Para chegar à cidade, ficar e voltar para o posto Estrela, ele precisa de:
4 L + 10 L + 4 L = 18 L
Como já há 1 L que restou no tanque, ele deve reabastecer 17 L.
Resposta Questão 8
Alternativa D
Como a escala é proporcional, montando a proporção, temos que:
\(\frac{1,4}{16,8}=\frac{2,2}{x}\)
\(1,4x=2,2\cdot16,8\)
\(1,4x=36,96\)
\(x=\frac{36,96}{1,4}\)
\(x=26,4\)
A largura é 26,4. Agora, calculando o comprimento:
\(\frac{1,4}{16,8}=\frac{3,4}{y}\)
\(1,4y=16,8\cdot3,4\)
\(1,4y=57,12\)
\(y=\frac{57,12}{1,4}\)
\(y=40,8\)
Então, a largura e o comprimento são, respectivamente, 26,4 cm e 40,8 cm.
Resposta Questão 9
Alternativa E
Podemos notar que existe uma relação, de fato, entre a quantidade de cigarros consumidos e os casos de câncer. Entretanto, não há uma proporção, pois existem intervalos que são contínuos no gráfico — de 1 até 14 cigarros consumidos diariamente, por exemplo.
Resposta Questão 10
Alternativa B
Sabemos que:
\(43k+42k+30k+24k+21k=800.000\)
Calculando o valor de k, temos que:
\(160k=800.000\)
\(k=\frac{800.000}{160}\)
\(k=5000\)
O filho que obteve a maior parte recebeu 43k:
\(43\cdot5000=215.000\)
Resposta Questão 11
Alternativa C
A soma dos ângulos internos de um triângulo é igual a 180°. Sendo k o coeficiente de proporção:
\(2k+3k+4k=180°\)
\(9k=180°\)
\(k=\frac{180°}9\)
\(k=20°\)
O menor ângulo mede 2k, logo sua medida é de:
\(2k=2\cdot20=40°\)
Resposta Questão 12
Alternativa A
O tempo e o número de pessoas nesse caso são grandezas inversamente proporcionais. Montando as proporções, percebemos que 4 está para 3 assim como 2 está para x, sendo que x é o tempo. Invertendo a segunda fração, pelo fato de ela ser inversamente proporcional, temos que:
\(\frac{4}{x}\ =\ \frac{2}{3}\)
\(2x=4\cdot3\)
\(2x\ =12\)
\(x=\frac{12}{2}\)
\(x=6\ \)



