Questão 1
Analise as sequências a seguir:
A – (1, 4, 7, 10, 13)
B – (1, 1, 1, 1, 1, 1)
C – (9, 3, -3, -9, -15...)
D – (1, 0, -1, 2, -2, 3, -3)
Sobre as sequências, podemos afirmar que:
A) Todas são progressões aritméticas.
B) Somente A e C são progressões aritméticas.
C) Somente D não é uma progressão aritmética.
D) Somente B e D são progressões aritméticas.
E) Nenhuma das sequências representa uma progressão aritmética.
Questão 2
Os ganhos de uma empresa, ao decorrer do ano, foram de R$800.000 no primeiro mês, e, a cada mês, houve um aumento de R$15.000 em relação ao mês anterior. Caso essa tendência seja mantida durante todos os meses, o lucro mensal dessa empresa, em dezembro, será de:
A) R$165.000
B) R$180.000
C) R$816.500
D) R$965.000
E) R$980.000
Questão 3
A altura de uma planta, em centímetros, ao decorrer dos dias, foi anotada e organizada conforme a tabela seguinte:
|
Tempo (dias) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Altura |
3,0 |
5,5 |
8,0 |
10,5 |
13,0 |
15,5 |
18,0 |
20,5 |
23,0 |
Se esse comportamento de crescimento for mantido, essa planta terá a altura de 65,5 cm após:
A) 20 dias
B) 22 dias
C) 23 dias
D) 25 dias
E) 26 dias
Questão 4
Cris decidiu ser uma influenciadora digital, e, para isso, ela criou uma conta nas redes sociais. Realizando a divulgação para os seus amigos mais próximos, logo no primeiro dia, ela conseguiu o marco de 40 seguidores. Após esse marco, no segundo dia, ela conseguiu mais 14 seguidores, no terceiro dia também, e assim sucessivamente durante toda a primeira semana. Se esse comportamento for mantido, ou seja, se ela conseguir 14 seguidores por dia, qual será a quantidade de seguidores ao final de 30 dias?
A) 446
B) 406
C) 400
D) 396
E) 380
Questão 5
Um atleta de alta performance tem se preparado para a disputa da Maratona do Rio, que possui atualmente um percurso de 42 km. Para isso, ele começou percorrendo 14 km no primeiro dia, e, a cada dia, ele acrescentou 5 km em relação ao dia anterior. A distância total percorrida por esse atleta durante uma semana de treino é de:
A) 44 km
B) 244 km
C) 193 km
D) 198 km
E) 203 km
Questão 6
No ano de 2020, infelizmente, as Olimpíadas foram adiadas devido à pandemia de COVID-19. Sabendo que as Olimpíadas ocorrem de 4 em 4 anos e supondo que, em 2021, tenhamos esse evento, e que, até 2100, ele não passe por um novo adiamento, a quantidade de Olimpíadas que terão acontecido nesse intervalo será de:
A)18
B)19
C) 20
D) 21
E) 22
Questão 7
Sobre progressões aritméticas, julgue como verdadeiro ou falso as afirmativas a seguir:
I – Uma progressão aritmética é crescente quando sua razão é positiva.
II – Uma progressão aritmética é constante quando sua razão é zero.
III – Uma progressão aritmética é decrescente quando sua razão é negativa.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são verdadeiras.
E) Nenhuma das afirmativas é verdadeira.
Questão 8
Uma empresa faturou R$150.000 no primeiro ano, R$ 148.000 no segundo ano, R$146.000 no terceiro ano, e assim sucessivamente. Durante a primeira década de existência dessa empresa, ela faturou um total de:
A) 1.500.000
B) 3.500.000
C) 3.780.000
D) 1.410.000
E) 1.280.000
Questão 9
(Enem) O número mensal de passagens de uma determinada empresa aérea aumentou no ano passado nas seguintes condições: em janeiro foram vendidas 33.000 passagens; em fevereiro, 34.500; em março, 36.000. Esse padrão de crescimento manteve-se para os meses subsequentes. Quantas passagens foram vendidas por essa empresa em julho do ano passado?
A) 38.000
B) 40.500
C) 41.000
D) 42.000
E) 48.000
Questão 10
(Enem 2018) A prefeitura de um pequeno município do interior decide colocar postes para iluminação ao longo de uma estrada retilínea, que inicia em uma praça central e termina numa fazenda na zona rural. Como a praça já possui iluminação, o primeiro poste será colocado a 80 metros dela, o segundo, a 100 metros, o terceiro, a 120 metros, e assim sucessivamente, mantendo-se sempre uma distância de 20 metros entre os postes, até que o último poste seja colocado a uma distância de 1.380 metros da praça.
Se a prefeitura pode pagar, no máximo, R$ 8.000 por poste colocado, o maior valor que poderá gastar com a colocação desses postes é:
A) R$512.000
B) R$520.000
C) R$528.000
D) R$552.000
E) R$584.000
Questão 11
(Enem) As projeções para a produção de arroz no período de 2012-2021, em uma determinada região produtora, apontam para uma perspectiva de crescimento constante da produção anual. O quadro apresenta a quantidade de arroz, em toneladas, que será produzida nos primeiros anos desse período, de acordo com essa projeção.
|
Ano |
Projeto da produção (t) |
|
2012 |
50,25 |
|
2013 |
51,50 |
|
2014 |
52,75 |
|
2015 |
54,00 |
A quantidade total de arroz, em toneladas, que deverá ser produzida no período de 2012 a 2021, será de:
A) 497,25
B) 500,85
C) 502,87
D) 558,75
E) 563,25
Questão 12
(Ita) O valor de n que torna a sequência
2 + 3n, -5n, 1 – 4n
uma progressão aritmética pertence ao intervalo
a) [-2, -1].
b) [-1, 0].
c) [0, 1].
d) [1, 2].
e) [2, 3].
Resposta Questão 1
Alternativa C
Para que uma sequência seja uma progressão a aritmética, a diferença de um termo com o seu antecessor tem que ser constante, essa diferença é o que chamamos de razão r.
Analisando cada uma delas, temos que:
A – (1, 4, 7, 10, 13) é uma progressão aritmética:
4 – 1 = 3
7 – 4 = 3
10 – 7 = 3
13 – 10 = 3
É fácil ver que, de um termo para o seu anterior, a diferença é sempre 3, o que faz com que essa seja uma PA de razão 3.
B – (1, 1, 1, 1, 1, 1) é uma progressão aritmética:
1 – 1= 0
Note que a diferença entre um termo e o outro é sempre igual a 0, logo, essa é uma progressão arimética de razão 0.
C – (9, 3, -3, -9, -15...) é uma progressão aritmética:
3 – 9 = -6
-3 – 3 = -6
-9 – (-3) = -9 + 3 = -6
-15 – (-9) = -15 + 9 = -6
Note que a diferença entre um termo e o outro é sempre igual a -6, logo, essa é uma progressão arimética de razão -6.
D – (1, 0, -1, 2, -2, 3, -3) não é uma progressão aritmética:
0 – 1 = -1
-1 – 0 = -1
2 – (-1) = 2 + 1 = 3
Já é possível perceber que essa sequência não é uma progressão aritmética, pois a diferença entre os termos não é constante.
Resposta Questão 2
Alternativa D
Analisando a situação, é possível percebermos que o primeiro termo a1 = 800.000 e que a razão dessa progressão r = 15.000.
Utilizando a fórmula do termo geral de uma P.A., queremos encontrar os lucros no 12º mês (dezembro), ou seja, o termo a12.
Sabemos que:
an = a1 + (n – 1) r
Substituindo os valores conhecidos, temos que:
a12 = 800.000 + (12 – 1) 15.000
a12 = 800.000 + 11 · 15.000
a12 = 800.00 + 165.000
a12 = 965.000
Resposta Questão 3
Alternativa E
Analisando o comportamento, podemos notar que a sequência que representa a altura, ao decorrer do tempo, é uma PA, pois, a cada dia, há um crescimento de 2,5 cm, ou seja, a razão da PA é 2,5 cm.
Queremos encontrar um tempo n tal que an = 65,5 cm. Sendo assim, vamos utilizar a fórmula do termo geral de uma PA.
an = a1 + ( n – 1) r
Temos que an = 65,5; r = 2,5; e a1 = 3, então:
65,5 = 3 + (n – 1) · 2,5
65,5 – 3 = (n – 1) · 2,5
62,5 = (n – 1) · 2,5
62,5 = 2,5n – 2,5
62,5 + 2,5 = 2,5n
65 = 2,5n
65 : 2,5 = n
n = 26
Resposta Questão 4
Alternativa A
A sequência formada pela quantidade de seguidores é uma P.A., cujo primeiro termo é 40 e cuja razão é 14. Queremos encontrar o termo a30.
De modo geral, sabemos que:
an = a1 + (n – 1) r
Substituindo pelos valores conhecidos, temos que:
a30 = 40 + (30 – 1) 14
a30 = 40 + 29 · 14
a30 = 40 + 406
a30 = 446
Resposta Questão 5
Alternativa E
Queremos calcular a soma dos termos de uma P.A. que é dada pela fórmula a seguir:
![]()
Queremos, nesse caso, a soma dos sete primeiros termos da sequência, ou seja n = 7. Conhecido o valor de n, o valor inicial a1 = 14 e a razão r = 5, encontraremos o valor de a7.
an = a1 + (n – 1) r
a7 = 14 + (7 – 1) · 5
a7 = 14 + 6 · 5
a7 = 14 + 30 = 44
Agora é possível calcular S7:
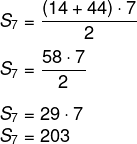
Na primeira semana, o atleta percorreu, ao todo, 203 km.
Resposta Questão 6
Alternativa C
Queremos o valor de n, tal que an seja igual a 2100 ou o valor que chegue mais próximo a ele.
Sabendo que:
an = 2100
a1 = 2021
r = 4
Sendo assim, faremos:
an = a1 + (n – 1) r
2100 = 2021 + (n – 1) · 4
2100 – 2021 = (n – 1) · 4
79 = (n – 1) · 4
79 = 4n – 4
79 + 4 = 4n
83 = 4n
n = 83/4
n = 20,75
Note que a parte inteira é o número de Olimpíadas que já ocorreram, logo, o número de Olimpíadas, nesse intervalo de tempo, é igual a 20.
Resposta Questão 7
Alternativa D
O comportamento de uma progressão arimética é dado de acordo com a sua razão, então temos três casos:
Se r positivo → a P.A. é crescente.
Se r igual a zero → a P.A. é constante.
Se r negativo → a P.A. é decrescente.
Sendo assim, todas as afirmativas são verdadeiras.
I – Verdadeira
II – Verdadeira
III – Verdadeira
Resposta Questão 8
Alternativa D
É possível perceber que a sequência de faturamento comporta-se como uma P.A. de razão r igual a -2.000 e que o primeiro termo a1 = 150.000. Para realizar a soma dos dez primeiros termos dessa sequência, utilizaremos a fórmula da soma de uma P.A. finita, que é:
![]()
Para aplicar a fórmula, primeiro é necessário encontrarmos o termo a10.
an = a1 + (n – 1) r
a10 = 150.000 + (10 – 1) (-2.000)
a10 = 150.000 + 9 (-2.000)
a10 = 150.000 – 18.000
a10 = 132.000
Substituindo os valores conhecidos na fórmula da soma dos termos de uma P.A.:
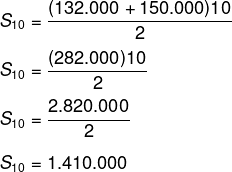
Resposta Questão 9
Alternativa D.
Analisando o comportamento da venda de passagens, percebe-se que, de janeiro para fevereiro, houve um aumento de 1.500, e o mesmo aconteceu de fevereiro para março. Dessa forma, se esse padrão for mantido, temos uma P.A. de razão 1.500 e primeiro termo 33.000. Queremos encontrar a quantidade de passagens vendidas em julho, que é o sétimo mês do ano, ou seja, vamos calcular o a7.
an = a1 + (n – 1) r
a7 = 33.000 + (7 – 1) · 1.500
a7 = 33.000 + 6 · 1.500
a7 = 33.000 + 9.000
a7 = 42.000
Resposta Questão 10
Alternativa C
Primeiro é necessário encontrarmos a quantidade de postes que serão colocados. Note que a sequência que mede a distância do poste em relação à praça é uma P.A., pois, para cada poste em relação ao anterior, há um aumento de 20 metros nessa distância, logo, r = 20. Para saber a quantidade de postes necessários, vamos calcular o valor de n para an = 1380, que é a distância do último poste. Note que o primeiro termo da sequência é 80, então temos que:
an = a1 + (n – 1) r
1380 = 80 + (n – 1) · 20
1380 = 80 + 20n – 20
1380 – 80 + 20 = + 20n
1320 = 20n
1320 : 20 = n
n = 66
Como o valor máximo de um poste é R$ 8000, então 66 · 8000 = 528.000.
Resposta Questão 11
Alternativa D
Analisando a sequência formada pelo projeto de produção, é possível perceber que, de um mês para o outro, o aumento é sempre o mesmo — 1,25 toneladas. O que faz com que essa sequência seja uma P.A. Sendo 2012 o primeiro termo, o ano de 2021 será o décimo termo dessa sequência, logo, queremos a soma dos dez primeiros termos dessa progressão. Para isso, primeiro vamos calcular o termo a10. Conhecendo a razão r = 1,25 e o primeiro termo a1 = 50,25, temos que:
an = a1 + (n – 1) r
a10 = 50,25 + (10 – 1) · 1,25
a10 = 50,25 + 9 · 1,25
a10 = 50,25 + 11,25
a10 = 61,50
Agora, conhecendo o décimo termo, realizaremos a soma dos dez primeiros termos da P.A.
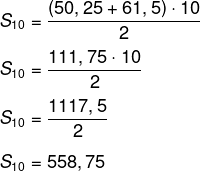
Resposta Questão 12
Alternativa B
Para que essa sequência seja uma progressão arimética, sabemos que a2 – a1 = a3 – a2, pois a diferença de um termo com o seu antecessor é sempre constante.
Sendo assim, temos que:
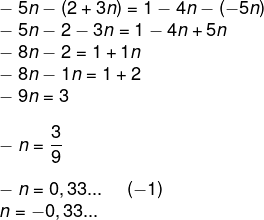
O valor encontrado para n está entre -1 e 0.



